第8章 运动
§8-1 运动的描述
为了找出物体随时间而发生的各种变化所遵循的规律,我们必须描述 这些变化,并用某种方式把它们记录下来。在物体中要观察的最简单的变化是物体的位置随时间的明显改变,我们把它称之为运动。让我们考虑某一个带有我们能观察它,并将它称为一个点的恒定标记的固体。我们将讨论这个小标记的运动(这个小标记可以是一辆汽车的散热器盖子,或一个下落球的球心),并将试图描述它在运动以及如何运动这一事实。
这些例子看来似较一般,但在描述其变化时,也有许多要小心对付之处。有些变化,例如,一朵缓慢漂移但迅速形成或迅速蒸发的云的漂移速率,或者一个女人思想上的变化,要描述它们就比描述在固体上一点的运动困难得多。我们不懂得分析思想上发生变化的简单方法,不过由于云可以用许多分子来表示或描述,或许在原则上我们能够通过描述云中所有个别分子的运动来描述云的运动。同样,甚至思想上的变化或许也与大脑内原子的变化有类似之处,但我们对此尚一无所知。
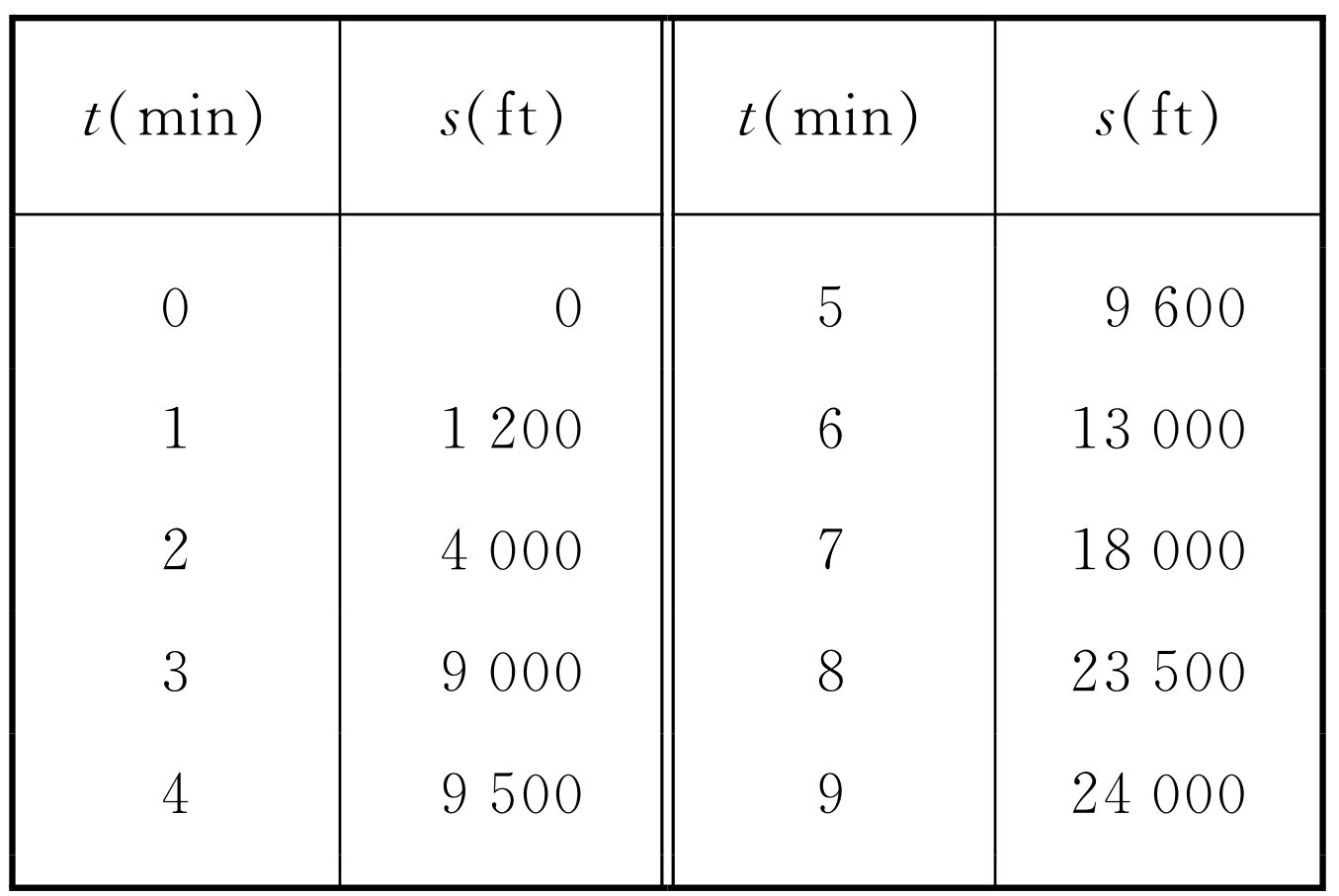
总而言之,这就是我们为什么要从点的运动开始研究的原因;也许我们应当把它们想象为原子,但在开始时粗略一些可能更妥当。我们把它们简单地想象为某一类小的物体——所谓小,是指与运动的距离相比较而言。比如,在描述一辆开过100 km的汽车的运动时,就不必去分汽车的前部和后部。的确,这里有一点儿差别,但粗略地看我们只讲“汽车”的运动,同样,我们选择的点不是绝对的点也丝毫没有关系;就我们现在的目的来说,没有必要极其精确。还有,在初次考察这个课题时,我们将不考虑世界的三维性。我们将只集中注意在一个方向上的运动,就像在一条公路上行驶的汽车那样。当我们知道了如何描写一维运动后,就将回到三维中去。现在,你们会说:“这尽是一些琐碎的事,”确实如此。那么,我们怎样来描述这样的一维运动,比方说,汽车的运动呢?没有比这更简单的了。有许多可能的方式,下面是其中之一。为了确定不同时刻汽车的位置,我们测量它与起点的距离,并记下所有的观测。在表8-1中,s 表示汽车离起点的距离,单位是英尺,t 表示时间,单位是分。表中的第一行表示零距离和零时间——即汽车尚未出发。1分钟后,出发并开过了1 200 ft。在2分钟内,它开得更远——注意汽车在第2分钟开过了更大的距离——汽车在加速前进;但在第3和第4分钟甚至一直到第5分钟之间发生了什么事情——也许是遇到红灯停了下来?然后它再次加速,在第6分钟末开过13 000 ft,在第7分钟末开过18 000 ft,在第8分钟开过23 500 ft,在第9分钟它只前进到24 000 ft,因为在最后一分钟它被警察拦住了。
表8-1
这就是一种描写运动的方式,另一种方式是利用曲线图。如果我们以横轴表示时间,纵轴表示距离,就得到如图8-1那样的一条曲线。当时间增加时,距离也增加,开始很慢,然后较快,在4分钟前后又很慢,以后几分钟内又再加快,最后在第9分钟时,看来像停止增加。这些情况不用表也能从图上观察到。显然,为了描述完全起见,人们还必须知道,在那些半分钟的标记处,汽车开到了那里。但是我们假定这个曲线图意味着在所有的居间时刻汽车都具有某个位置。
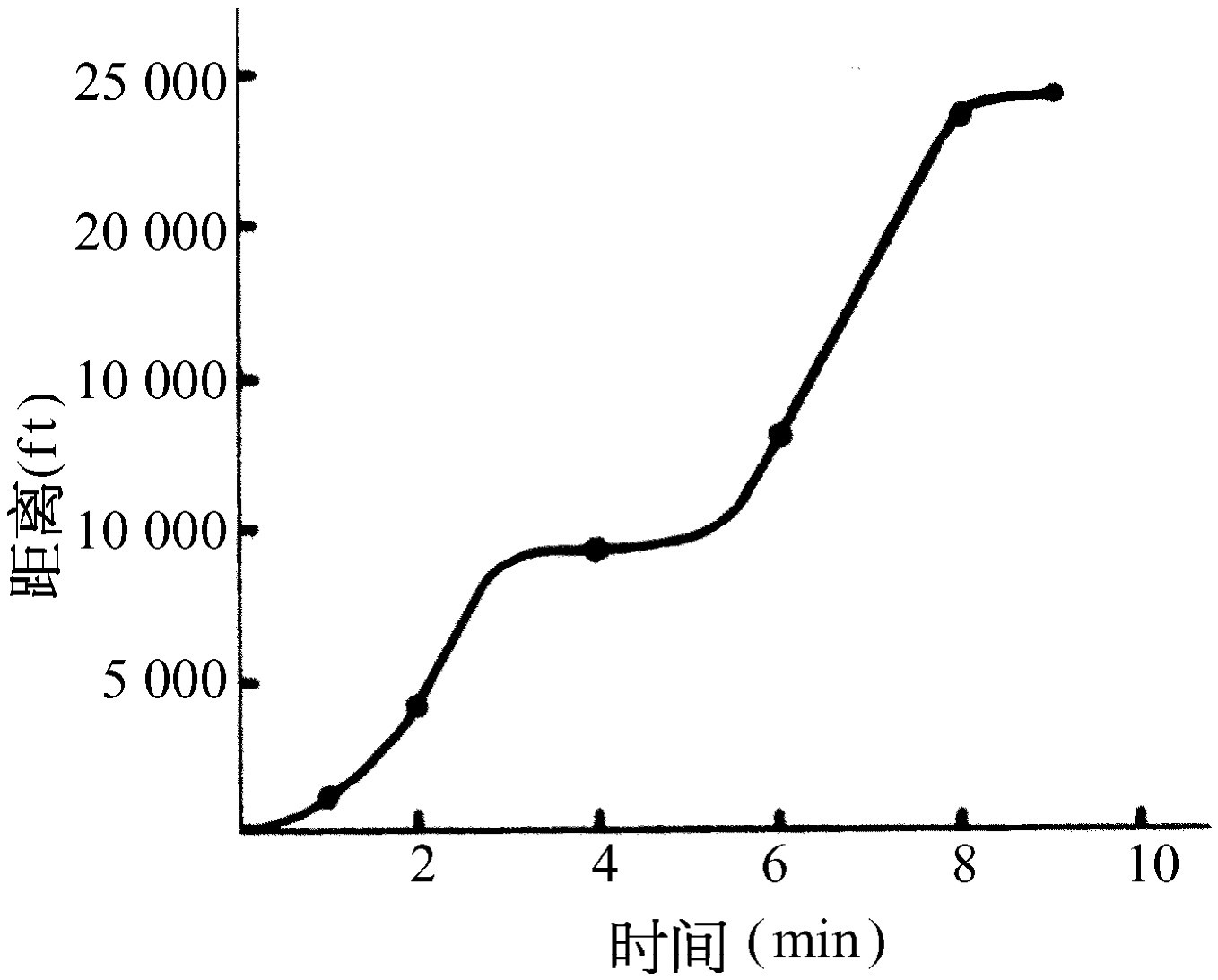
图8-1 汽车的距离-时间曲线
汽车的运动是复杂的。我们取某个以比较简单的方式运动的东西,比如说一个下落的小球,作为另一个例子。它遵循较简单的规律。表8-2列出落体的时间(以秒为单位)和距离(以英尺为单位)。在零秒时,小球从0 ft开始下落,在第1秒末落下16 ft,在第2秒末落下64 ft,在第3秒末落下144 ft,等等。如果将表上的数字作图,就得到图8-2所示的一条漂亮的抛物线。这条曲线的公式可以写为
s =16t 2 .(8.1)
表8-2
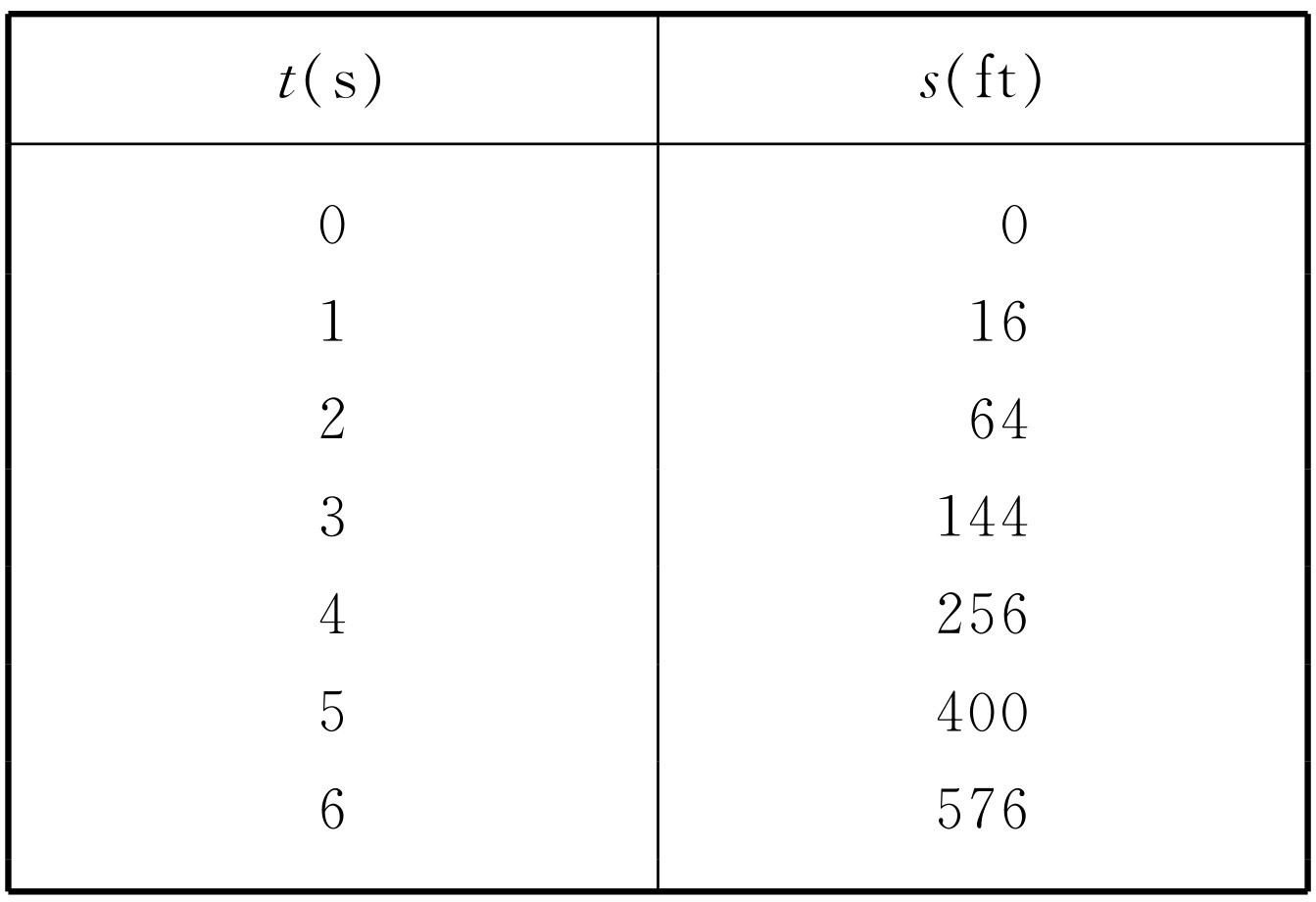

图8-2 落体的距离-时间曲线
这个公式使我们可以计算小球在任何时刻的距离。你们或许会说,对第一个曲线图也应当有个公式。实际上,人们也可以抽象地把这样一个公式写成
s =f (t ),(8.2)
它表示s 是某个依赖于t 的量,或用数学术语来说,s 是t 的函数。由于我们不知道这个函数是什么,因此无法以确定的代数形式写下来。
现在我们已经看到了两个用非常简单的思想就能适当地描述的运动的例子——没有什么难以捉摸之处。然而,难以捉摸之处还是有的,有几处 。首先,时间 和空间 究竟意味着什么?结果表明,这些深刻的哲学命题在物理学上必须十分小心地加以分析,而这并不是容易做到的。相对论表明我们关于空间和时间的观念并不如人们乍一看来可以想象的那么简单。然而,就我们当前的目的而论,对我们在开始时所要求的精确度来说,我们毋需十分小心地去精确地定义事物。或许你们要说:“这很糟糕,我听说过在科学上我们必须精确地定义每一件事。”我们不可能精确地定义任何事物 !如果强求如此,只会使我们陷入像某些哲学家那样的思想僵化,他们面对面坐着,一个对另一个说:“你不知道你在讲些什么!”第二个说:“你所谓的‘知道 ’是什么意思呢?你所谓的‘讲 ’是什么意思呢?你所谓的‘你 ’又是什么意思呢?诸如此类。”为了能够进行建设性的讨论,我们必须一致赞同我们所谈论的大致是同一件事。你们对于时间的了解已能满足我们目前的需要,但必须记住,还有一些微妙和难以捉摸的事情需要讨论,我们将在以后进行。
前面所涉及的另一个难以捉摸之处是能够设想我们正在观察的动点总是位于某处(当然,当我们注视它时,它在那里,但当我们看别处时,它可能不在那里了)。现在知道,在原子的运动中,这个观念也是错误的,我们不可能在一个原子上找到一个标记并观察它的运动。这种微妙的情况我们将在量子力学中去仔细讨论,但是在引进复杂性之前,我们将首先了解一下这些问题是什么,然后 才能较好地按照这个题材的更现代的知识进行修正。因此,关于时间和空间,我们将采用一种简单的观点。我们大致知道这些概念是怎么一回事,而那些驾驶汽车的人则知道速率指的是什么。
§8-2 速率
即使我们大致知道“速率”的含义,也仍有某些相当奥妙的难以捉摸之处;须知甚至博学的希腊人也从未能恰当地描述牵涉到速度的问题。当我们试图精确地领会“速率”的含义时,就会出现难以捉摸之处。希腊人对这个问题是非常混乱的,因而必须在希腊人、阿拉伯人与巴比伦人的几何学与代数学之外,发现一个新的数学分支才能解决这个问题。作为这种难点的一个例证,试用纯代数方法来解这样一个问题:一个气球正在膨胀,它的体积以100 cm3 ·s-1 的比率增加;当气球体积为1 000 cm3 时,气球半径增加的速率是多少?希腊人多少有点被这样的问题弄糊涂了。当然,这是被某些思想混乱的人所促成的。为了指出在某一时刻有关速度方面的推理中存在着困难,泽诺(Zeno)提出了一大堆佯谬,我们将举其中的一个来说明他的关于思考运动时存在着明显困难的论点。“请听这样的论点”,他说:“阿基利斯(Achilles)比乌龟跑得快10倍,但他却永远抓不住乌龟。因为,假定他们开始赛跑时,乌龟在阿基利斯前面100 m,那么当阿基利斯跑了100 m而到达乌龟原来所在的地方时,乌龟已经以他的快慢的1/10前进了10 m。现在,阿基利斯又得跑另一个10 m以便赶上乌龟,但在到达该段路程的终点时,他发现乌龟仍在他前面1米;当他再跑1 m时,他又发现乌龟依然在他前面10 cm,如此下去,直至无穷 。因此,在任何时刻乌龟总是在阿基利斯前面,阿基利斯永远追不上乌龟。”这段论证错在哪里?它错在认为一段有限的时间可以被分为无限多的段,正如一段线长不断地一分为二可以被分成无限多的小段一样。因此,虽然(在论证中)到阿基利斯追上乌龟的那个点有无限多步,但这并不意味着时间 也有无限的数量,从这个例子我们可以看到,在有关速度的推理中的确存在一些难以捉摸的地方。
为了以更为清楚的方式来领会这种微妙的情况,我讲一个你们肯定听到过的笑话。坐在汽车里面的一位太太在某个地点被警察拦住了,警察走过来对她说:“太太,你刚才的车速是60 mi·h-1 !”她反驳说:“先生,这是不可能的,我刚才只开了7分钟。这真是天大的笑话!我开车还没有到一小时,怎么可能走60 mi呢?”假如你是警察的话你该如何回答她呢?当然,如果你真是那个警察,那就没有什么疑难之处,很简单,你会说:“对审判员讲去!”但是,假若我们没有这条退路,而是更公正和理智地对待这个问题,企图向这位太太解释所谓她的车速达60 mi·h-1 的说法是什么意思,那么我们的含义究竟 是什么呢?我们可以说:“太太,我们的意思是:如果你继续像现在这样开车,在下一个小时里你将开过60 mi。”她会答道:“嗯,我的脚已经离开油门,汽车已慢了下来,所以如果我继续这样开下去,不会超过60 mi的。”或者,我们考虑一个自由下落的小球,如果这个小球保持它正在进行的运动方式的话,我们想要知道它在第三秒时的速率有多大。这意味着什么呢?是继续加速 ,落得更快吗?不,应该是继续以同样的速度 运动。但这正是我们试图加以定义的东西!因为如果小球保持它现在正在进行的方式运动,那么它在以后就将继续保持这种方式运动。于是我们就需要更好地定义速度,究竟是什么必须保持一样呢?这位太太也可以这样来辩护:“如果我再继续保持现在的开车方式,那么过了一小时后,我就会撞到街道尽头的墙上了!”看来要说清楚我们的意思并不那么容易。
许多物理学家认为测量是唯一定义任何事物的方式。那么,显然,我们应当使用测量速率的仪器——速度计,并说:“看!太太,你的速度计的读数指到60。”可是她说:“我的速度计坏了,根本不能读数。”这是否表示汽车停着不动呢?我们相信,在我们造出速度计之前,就存在某种要测量的东西。只有这样,我们才可以说:“速度计走得不准,”或“速度计坏了。”如果速度没有与速度计无关的含义,上面所讲的就是毫无意义的废话。所以,显然在我们的头脑中存在着一种与速度计无关的概念,速度计只是用来使这个概念计量化。所以,还是让我们来看看是否能得到这个概念的更好的定义。我们可以说:“嗯!固然在你的车子开了一个小时以前,你就会撞到墙上,但是如果你开了一秒钟,你就会通过88 ft的距离。太太,你刚才的车速正是88 ft·s-1 ,如果继续下去,下一秒钟也将开过88 ft,而那堵墙离这还远着呢。”她就说:“对,但是,没有一条法律禁止88 ft·s-1 的车速!只有一条禁止开60 mi·h-1 的法律。”“不过,”我们反驳道:“这是同一件事。”如果这确是 同一件事,又何必转弯抹角地大讲其88 ft·s-1 呢?事实上,自由落体甚至连一秒钟也不可能保持同样的运动方式,因为它的快慢在变化着,我们必须设法来定义速率。
现在看来,我们已经走上了正轨,似乎可以这样说:如果那位太太在另一个1/1 000 h内继续这样行驶,她将开过60 mi的1/1 000。换句话说,她无需继续开足1 h,主要在于,在某一瞬间 她正以这个速率开车。现在我们的意思是,只要她再多开一点点时间,那么汽车所通过的外加距离就和一辆以60 mi·s-1 的稳定 速率开动的汽车相同。也许88 ft·s-1 的观念是正确的,我们看看她在最后一秒钟开了多远,再除以88 ft,如果结果是1,那么速率就是60 mi·s-1 。换句话说,可以这样来求出速率:我们问在一个很短的时间内物体走过多远?把这一段距离除以时间就得到速率。但是应当把这段时间取得尽可能短,越短越好,因为在这段时间内有可能发生某种变化。假如我们将落体的时间取为一小时,这个概念就荒唐了。但若取为1 s,对汽车来说其结果就相当好,因为在这段时间内,汽车的快慢没有很大变化,但对落体来说就不行了。所以为了要得到越来越精确的速率,我们应当把时间间隔取得越来越小。我们应当做的是取百万分之一秒,并且用百万分之一秒去除以通过的距离。结果给出每秒的距离,这就是我们所谓的速度。因此我们可以用这个方式去定义它。这是对那位太太的成功的答案,或者更确切地说,它就是我们将要采用的定义。
上述定义包括了一个新的概念,这是一个不曾被希腊人以普遍形式所采用过的概念。这个概念是取无穷小距离 及相应的无穷小时间 ,求出它们的比值,并观察当我们所取的时间越来越小时,那个比值将发生什么情况。换句话说,当时间越取越小,以至无穷小 时,取所通过的距离除以所需的时间的极限。这个概念分别由牛顿和莱布尼茨发明,它开创了称为微分学 的新的数学分支。微积分的发明是为了描述运动,而它的第一个应用就是给“每小时开60 mi”作什么解释下一个定义。
让我们试试看把速度定义得更好一些。假设在一个短时间ε 内,汽车或其他物体通过一段短距离x ,则速度v 定义为
v =x/ε .
这是一个近似,当ε 取得越来越小,近似程度就越来越好。如果想用一个数学表示式,我们可以说速度等于在表示式x/ε 中,当ε 越来越小时的极限,即
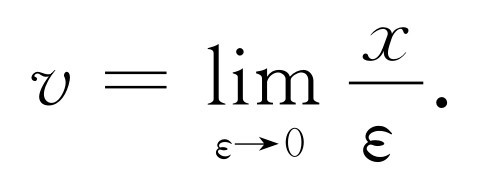 (8.3)
(8.3)
我们不可能对汽车里面的那位太太做同样的事情,因为那张表是不完全的。我们只知道她在各个间隔为1分钟的时刻的位置,我们能得到在第7分钟内她开车的速率是5 000 ft·min-1 这一大致的概念,但无法知道,在正好是第7分钟那个时刻,她是否已经加速运动,是否在第6分钟开始时速率是4 900 ft·min-1 ,而现在是5 100 ft·min-1 ,或者其他情况,因为我们没有获知其间的精确细节。因此只有以无穷个数据来完成这张表,我们才能真正从这样一张表来计算速度。另一方面,如果我们有一个完整的数学公式,就像在落体的情况下(8.1式)那样,就有可能计算速度,因为我们可以计算出在无论任何时刻的位置。
作为例子,我们来决定落体在5 s那个特定时刻的速度。一个方法是由表8-2中看出它在第五秒内的情况,它走了400-256=144 ft,因此它正以144 ft·s-1 下落;可是这是错误的,因为速率正在发生变化,在这段时间间隔内,平均来说是144 ft·s-1 ,但这个球在加速,因而实际上走得比144 ft·s-1 要快。我们希望弄清楚它的速度究竟有多快。在这个过程中涉及的方法如下:我们知道在5 s时球在那里。在5.1 s时,它总共走过的距离是16(5.1)2 =416.16 ft[见式(8.1)],在5 s内它已下落400 ft,在最后的1/10 s内它下落了416.16-400=16.16 ft。由于在0.1 s中通过16.16 ft与161.6 ft·s-1 是同一回事,这差不多就是速率,但还不完全正确。它究竟是5 s、5.1 s抑或是两者当中的5.05 s时的速度呢?或者说,是 什么时刻的速度?别管它——现在的问题是要求出在5 s时的速率,而我们还没有得到精确的答案。我们必须进一步去求。于是,我们比5 s多取千分之一秒,即5.001 s。再计算这时总共落下的距离
s =16(5.001)2 =16(25.010 001)=400.160 016 ft.
在最后0.001 s内球落下了0.160 016 ft,如以0.001 s除以这个数字。就得到速率为160.016 ft·s-1
。这个值更为接近,而且十分接近,但它仍不精确
。为了找出准确的速率,我们必须做什么,是很明显的。为了完成这个数学过程,我们把问题提得略微抽象一点;要求出在一特定时刻t
0
时的速度,在上面的问题中,t
0
就是5 s。现在在t
0
时刻的距离,我们称为s
0
是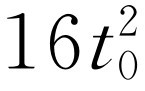 ,或在这个情况下是400 ft。为了求出速度,我们问:“在t
0
+(一点点),即t
0
+ε
时刻物体在何处?”新位置是
,或在这个情况下是400 ft。为了求出速度,我们问:“在t
0
+(一点点),即t
0
+ε
时刻物体在何处?”新位置是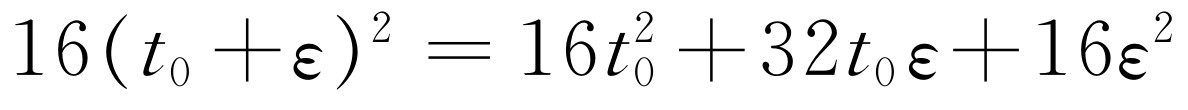 ,于是它比以前走得更远了,因为以前它只是
,于是它比以前走得更远了,因为以前它只是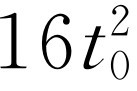 。这段距离我们称为s
0
+(多一点点)或s
0
+x
(如果x
是附加的一点点距离)。现在如果从在(t
0
+ε
)时刻的距离中减去在t
0
时刻的距离,我们就得出x
,即附加距离,为x
=32t
0
ε
+16ε
2
。我们对速度的第一次近似是
。这段距离我们称为s
0
+(多一点点)或s
0
+x
(如果x
是附加的一点点距离)。现在如果从在(t
0
+ε
)时刻的距离中减去在t
0
时刻的距离,我们就得出x
,即附加距离,为x
=32t
0
ε
+16ε
2
。我们对速度的第一次近似是
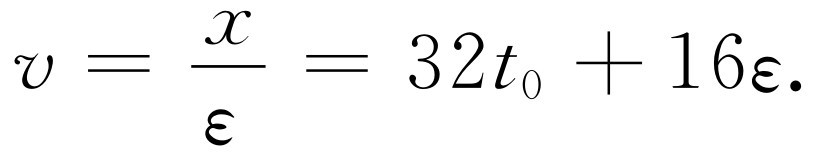 (8.4)
(8.4)
真正的速度是当ε 变到趋于0那么小时的比值x/ε 。换句话说,在作出比值后,我们取当ε 越来越小,即趋于0时的极限。(8.4)式化为
v (在时刻t 0 )=32t 0 .
在我们的问题中t 0 =5 s,故答案是v =32×5=160 ft·s-1 。在前面,我们曾相继取ε =0.1及0.001 s,所得到的v 值比这稍大一些,但现在我们看到,实际速度正好是160 ft·s-1 。
§8-3 速率作为导数
我们刚刚采用的步骤在数学上是经常要做的,因此为了方便起见,对量ε 和x 规定了特殊的符号。在这一符号中,上面所用的ε 改为Δt ,x 改为Δs 。Δt 表示“附加的一点t ”,并带有它能变得更小的含义。前缀Δ不是一个乘数,正如sin θ 不是s·i·n·θ 一样,它仅仅定义了一个时间增量,并使我们想起了它所具有的特性。Δs 对距离s 有类似的含义。因为Δ不是一个因子,因此在比值Δs /Δt 中不能消去而得出s /t ,正如比值sin θ /sin 2θ 不能消去成为1/2一样。在这种符号下,速度等于当Δt 变得越来越小时Δs /Δt 的极限,即
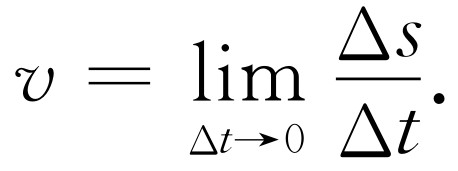 (8.5)
(8.5)
实际上这和我们前面使用ε 与x 的表达式(8.3)相同,但它的好处是表示某种东西在变化着,并且记录了什么东西正在发生变化。
顺便提一下,作为一个好的近似,我们还得到另一条定律:一个动点距离的变化是速度乘上时间间隔,或Δs =v Δt 。这个说法仅当速度在这个时间间隔内不变时才正确,而这个条件又只是在Δt 趋于0的极限情况下才成立。物理学家喜欢把它写为ds =v dt ,因为按他们的意思dt 是非常小的。根据这样的理解,这个表达式作为一个非常接近的近似是成立的。如果Δt 太长,速度在这段间隔内可能发生变化,因而这个近似就欠佳了。对趋于0的时间dt ,ds =v dt 严格成立。用这种符号我们可将(8.5)式写为
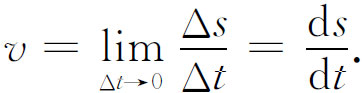
我们在上面得到的量ds /dt 叫做“s 对于t 的导数”(这个称呼有助于记下发生变化的过程),而求出它的复杂过程就称为求导,或求微商。单独出现的ds 和dt 称为微分。为了使你们熟悉用词,我们指出,我们已经找到函数16t 2 的导数,或16t 2 对于t 的导数是32t 。当我们习惯于这些词后,这些概念就更容易理解了。作为练习,让我们来求一个更复杂的函数的导数。我们考虑公式s =At 3 +Bt +C ,它可以描写一点的运动。字母A ,B ,C 表示常数,就像在熟知的二次方程一般形式中一样。从这个运动公式出发,我们希望求出在任何时刻的速度。为了以比较巧妙的方式求得它,我们把t 改为t +Δt ,并注意s 将随之变为s +某个Δs ;然后我们求出用Δt 来表示的Δs 。这就是说
s +Δs =A (t +Δt )3 +B (t +Δt )+C =At 3 +Bt +C +3At 2 Δt +B Δt +3At (Δt )2 +A (Δt )3 .
但由于
s =At 3 +Bt +C ,
因而
Δs =3At 2 Δt +B Δt +3At (Δt )2 +A (Δt )3 .
但是我们想要的不是Δs ,而是Δs 除以Δt 。将上述等式除以Δt ,得
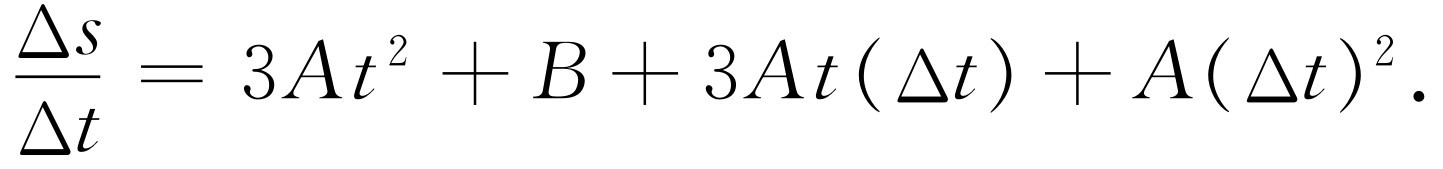
当Δt 趋于0时,Δs /Δt 的极限是ds /dt ,并等于
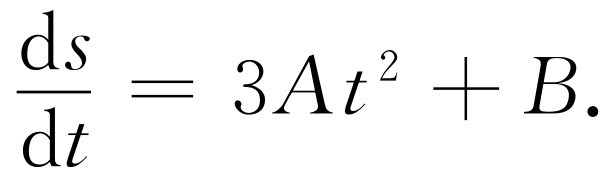
这就是微积分的基本运算过程,对函数求微商。这个过程甚至可以比上面所讲的更简单一些。当观察到这些展开式中含有Δt 的平方项、立方项或任何更高次幂时,这种项马上可以去掉,因为取极限时它们变为0。在稍微练习一下后,这个过程就显得方便了,因为我们知道把什么去掉。为了求出不同类型的函数的微商,有许多规则或公式。这些规则或公式可以记住,也可以在表中找到。表8-3就是一张简表。
表8-3 求导简表

§8-4 距离作为积分
现在我们讨论相反的问题。假定我们不是有一张距离的表,而是有一张从零开始,在不同时刻的速率表。对一个下落的球,这样的速率和时间表如表8-4所示。
表8-4 自由下落小球的速度

每分钟或每半分钟记录一次速度计的读数也可以对汽车的速度作出类似的表。假如我们知道汽车在任何时刻开得有多快,我们能确定它开了多远吗?这个问题恰好与上面所解决的问题相反,即给出速度而要求出距离。如果我们知道了速度,我们怎样找出距离呢?假定汽车的速度不是常数,而那位太太在某个时刻的速度是60 mi·h-1 ,然后慢下来,再加快,等等,我们如何来确定汽车走了多远呢?这很容易。我们使用同样的概念,并将距离表示成许多无穷小量之和。我们说:“在第一秒钟汽车的速度是如此如此,并由公式Δs =v Δt ,计算出它以这个速度在第一秒内走了多远。”而在下一秒钟内它的速度近似相同,但略有差别。我们可以用新的速率乘时间来计算出在下一秒钟内它走了多远。对每一秒钟我们都同样处理,直到路程的终点为止。现在我们就求得了一系列小距离,总距离将是所有这些小距离的和。这就是说,距离将是速率乘时间的和,或s =∑v Δt ,这里希腊字母∑表示累加。说得更确切一些,距离是在某一确定时刻,比方第i 个时刻的速度乘以Δt 以后的和。
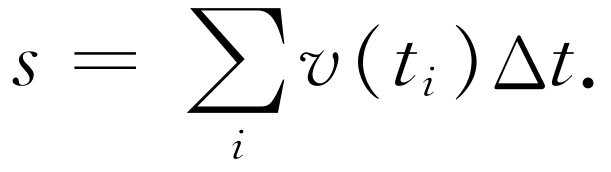 (8.6)
(8.6)
这里关于时间的规则是t i +1 =t i +Δt 。然而,我们用这个方法得到的距离是不准确的,因为在时间间隔Δt 内速度已发生变化。假定我们将时间取得足够短,和就是精确的了,于是我们将时间取得越来越小,直到获得所需要的精确度为止。真正的s 是
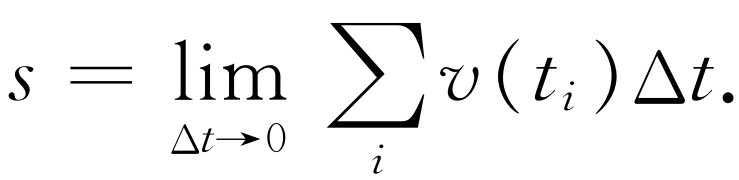 (8.7)
(8.7)
类似于微分符号,数学家们对这个极限也规定了一个符号。(8.7)式中的Δ变为d,以提醒我们时间是尽可能地短,于是速度就是在时刻t 的v ,累加则写成用拉长了的“s ”——∫[从拉丁文Summa(和)而来]表示的和,遗憾的是现在只称其为积分符号。于是我们可写出
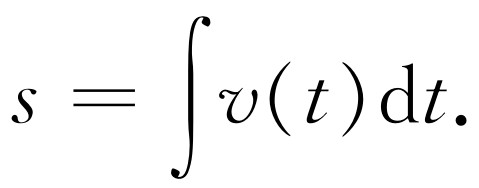 (8.8)
(8.8)
将所有这些项加起来的过程称为积分,它是微分的逆过程。这个积分的导数就是v ,所以一个运算符号(d)就消除了另一个运算符号(∫)。人们可以把求微商的公式反过来,以得出一些积分公式,因为它们彼此正好是相反的运算。于是,对所有类型的函数求微分,人们就可以得出他们自己的积分表。对每个微分公式,如果我们把它倒过来,就得到一个积分公式。
每个函数可以用解析的方法微分,即这个过程能用代数方法来进行,并得出某个确定的函数。但是,对任何随意给定的积分,却不可能用简单的方式写下一个解析解。你们可以计算一下,比如,上述的求和,再用更小的时间间隔Δt 进行计算,然后用更小的间隔等等,直到得到一个近乎正确的值。但一般说来,给定某个特殊的函数,就是不可能解析地找到它的积分是什么。人们可能老是想找到一个函数,当对它求微分后,能给出某个所希望的函数;但人们可能找不到它,而且从能用已命名的函数来表示的意义来说,它可能不存在。
§8-5 加速度
推导运动方程的下一个步骤是引进另一个超出速度概念的新概念,即速度的变化 。我们现在要问:“速度是如何改变 的?”在前几章中我们已经讨论过力产生速度变化的情况。你们或许在听到某辆汽车能在10 s内由静止达到60 mi·h-1 时很兴奋。从这样一种情况中我们可以看到速率变化有多快,但这只是平均的情况。我们现在将要讨论的是更为复杂的情况,即速度变化得有多快的问题,换句话说,在1 s内,速度的变化是每秒多少英尺,亦即每秒每秒多少英尺?我们前面已导出过落体速度的公式为v =32t ,其值列于表8-4中,现在我们要求出每秒钟速度改变多少,这个量称为加速度。
加速度的定义是速度的时间变化率。由前面的讨论,我们已经充分懂得,如同将速度写成距离对时间的微商那样,应将加速度写成微商dv /dt 。如果我们现在对公式v =32t 求微商,我们得出,对自由落体
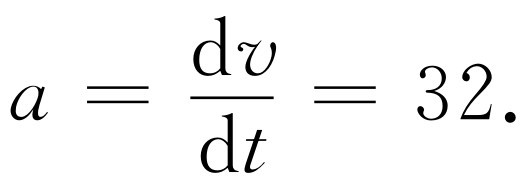 (8.9)
(8.9)
[为了求32t 的微商可利用前面问题中得出的结果,那里我们发现Bt 的微商就是B (常数)。这样,令B =32,马上得出32t 的微商是32]。这意味着落体的速度总是每秒改变32 ft·s-1 。从表8-4中亦可看到速度在每秒内增加32 ft·s-1 。这是一种非常简单的情况,因为加速度通常不是常数。在这里加速度是常数的原因是,作用在落体上的力是常数,而牛顿定律指出加速度与力成正比。
作为另一个例子,我们来求前面已经求过速度的那个问题中的加速度。由s =At 3 +Bt +C 出发,由于v =ds /dt ,我们得出
v=3At 2 +B .
因为加速度是速度对时间的导数,我们还需对上面最后一个表达式求微商。回忆一下,右方两项的微商等于各项微商之和的规则。为了对其中第一项求微商,注意到我们在对16t 2 求微商时,已求出过平方项的微商,因此不必再重复基本运算,其结果是将t 2 变成t ,并把数值系数加倍;我们假定这次发生的也是同样的情况,你们自己可以验证一下这个结果。于是3At 2 的微商是6At 。下一步我们对B 这个常数项求微商,按前述规则,B 的微商为0;因此,这一项对加速度无贡献。所以最后的结果是
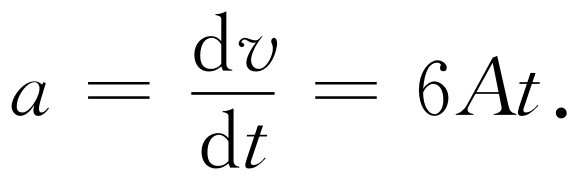
我们讲两个极有用的,可由积分得出的公式作为参考。如果一个物体由静止出发以匀加速度g 运动,它在任何时刻t 的速度为
v =gt .
在同一时间内它通过的距离是
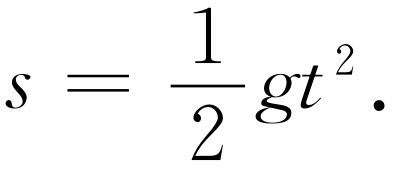
在写出微商时人们使用了各种数学符号。因为速度是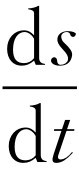 ,加速度是速度对时间的微商,我们也可写为
,加速度是速度对时间的微商,我们也可写为
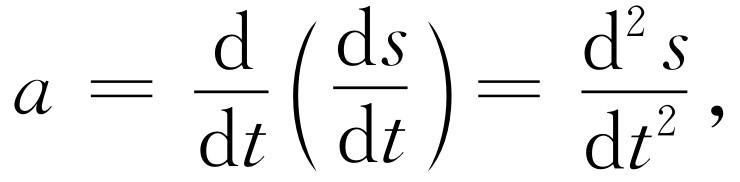 (8.10)
(8.10)
这是表示二阶导数的通常方法。
我们还有另一条规则:速度等于加速度的积分。这正是a =dv /dt 的逆过程;我们已经看到距离是速度的积分,所以距离可由加速度积分两次求出。
前面所讨论的运动只是一维情况,限于篇幅这里只简单讨论一下三维运动。考虑一个在三维空间中以无论什么方式运动的粒子P 。在本章开始时,我们从观察汽车在不同时间离出发点的距离,来展开对汽车的一维运动情况的讨论。然后讨论了用这些距离随时间的变化来表示速度,以及用速度的变化来表示加速度。我们可以类似地处理三维运动。先在二维图上说明运动,再将它推广到三维空间,这样做比较简单一些。我们建立一对互成直角的轴,然后由测量质点离每根轴多远来确定在任何时刻质点的位置。这样每个位置就可用x 距离和y 距离来表示,于是可列出表来描述运动,在表中将这两个距离都表示为时间的函数(将这个过程推广到三维空间时只需要再加上一根与前两根轴成直角的轴,并测量第三个距离,即z 距离。现在的距离不是从线,而是从坐标平面 量起)。在列出了x ,y 距离的表后,我们如何来确定速度呢?我们首先找出在每个方向上的速度分量。速度的水平部分,即x 分量,是x 距离对时间t 的微商,或
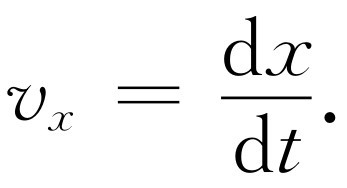 (8.11)
(8.11)
类似地,速度的垂直部分,或y 分量,是
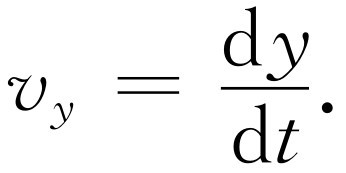 (8.12)
(8.12)
对第三维,
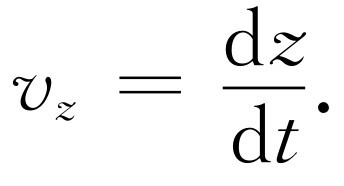 (8.13)
(8.13)
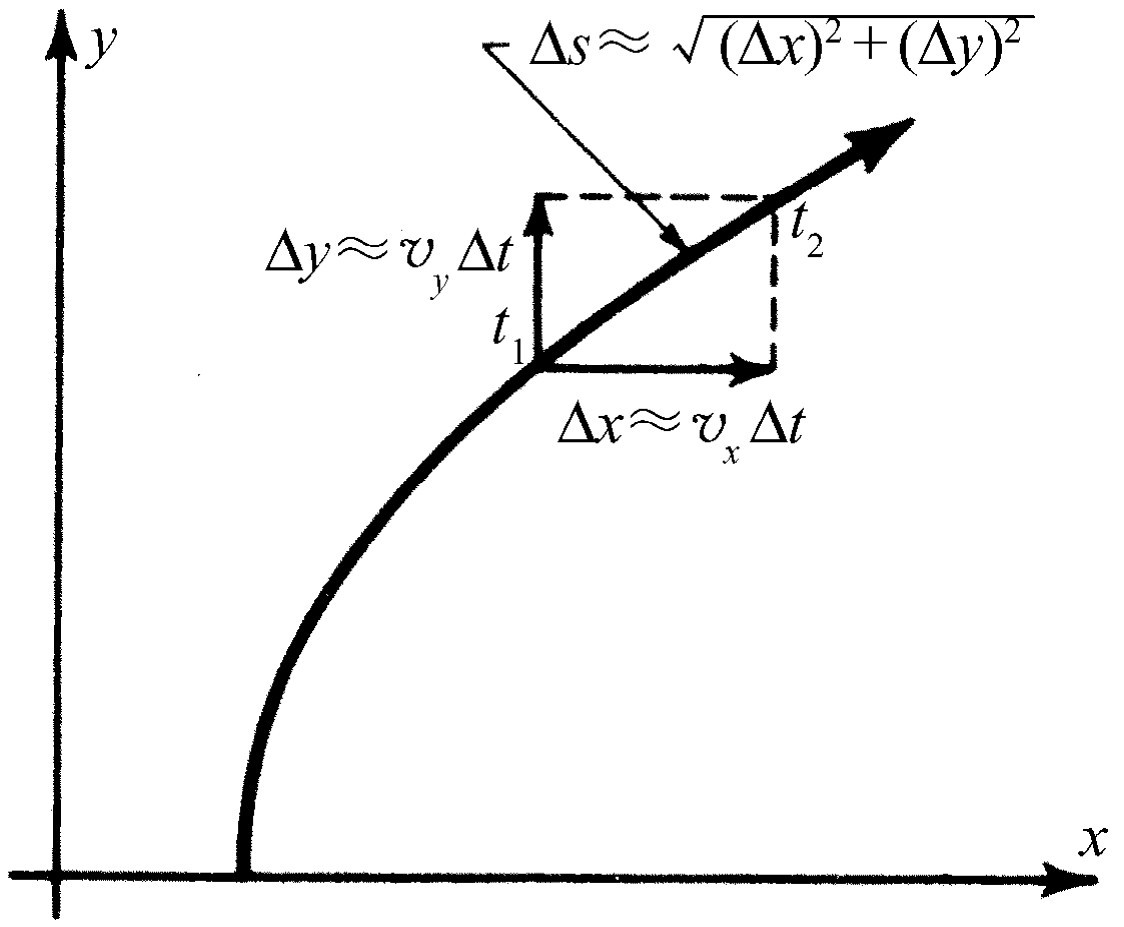
现在,给定了速度各分量,我们如何求沿实际运动路径的速度?在二维情况下,考虑质点两个彼此相隔短距离Δs 和短时间间隔t 2 -t 1 =Δt 的相继的位置。在Δt 时间内,质点水平运动的距离为Δx ≈v x Δt ,垂直运动的距离为Δy ≈v y Δt (符号“≈”读作“近似是”)。实际运动的距离近似是
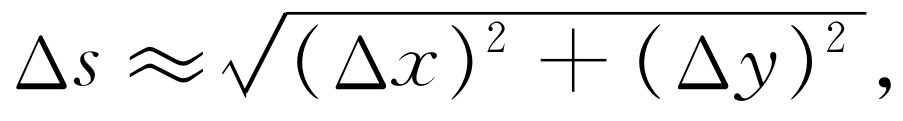 (8.14)
(8.14)
如图8-3所示。如本章开始时那样,在这个间隔内的近似速度可由Δs 除以Δt 并令Δt 趋于0而得出。于是得出速度为
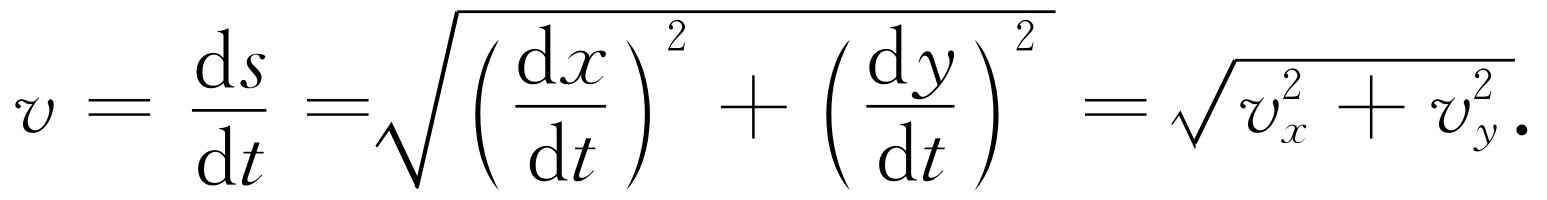 (8.15)
(8.15)
对于三维空间,结果是
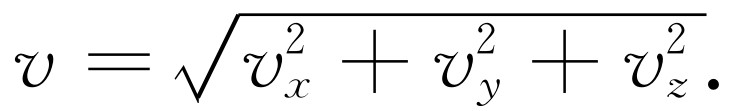 (8.16)
(8.16)
与定义速度的方法一样,我们可以定义加速度:可以得出加速度的x 分量a x 是速度的x 分量v x 的微商(即a x =d2 x /dt 2 ,x 对t 的二阶微商),等等。
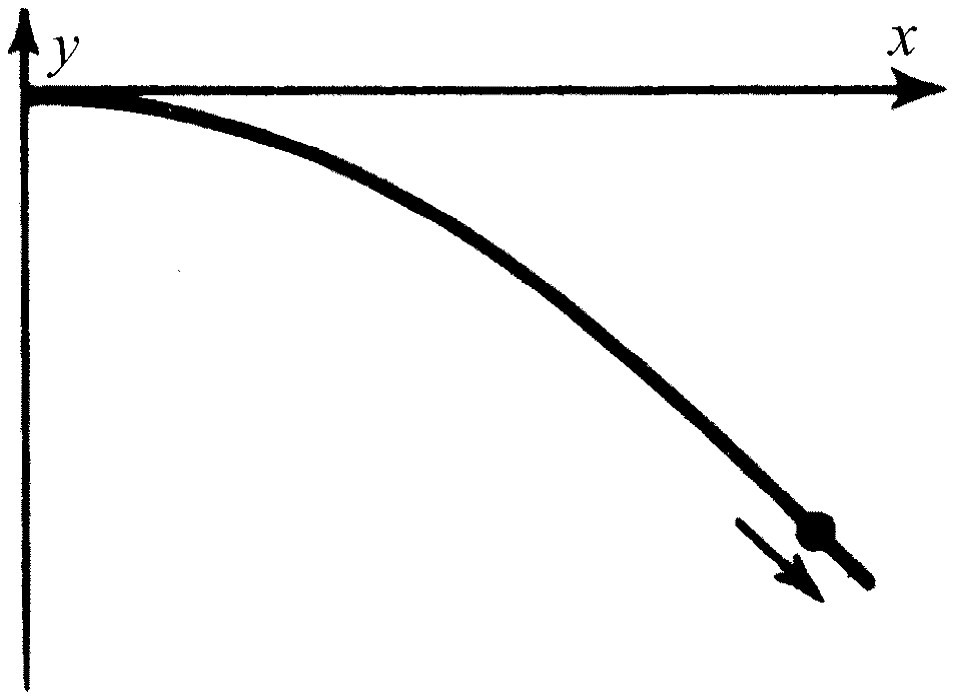
让我们考虑一个在平面内复合运动的良好例子。取一个在水平方向以匀速u 运动,同时在垂直向下的方向又以匀加速度(-g )运动的球;整个运动是怎样的呢?我们可以说dx /dt =v x =u 。因为速度v x 是常数,故
x =ut .(8.17)
而由于向下的加速度-g 是常数,球体落下的距离y 可写为
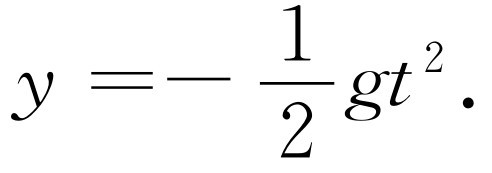 (8.18)
(8.18)
路程的曲线,即y 与x 之间的联系是怎样的呢?因为t =x /u ,我们可以从方程(8.18)消去t 。把它代入以后,求得
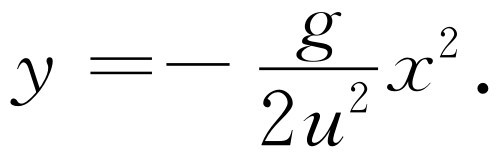 (8.19)
(8.19)
这个y 与x 之间的关系式可视为正在运动的小球的路径的方程。当画出这个方程的图形时,我们得到一条称为抛物线的曲线;向任何方向射出的自由落体都将沿着如图8-4所示的抛物线行进。