第18章 二维空间中的转动
§18-1 质心
在前面几章中,我们研究了点或者是小粒子的力学,在那里不涉及它们的内部结构。在下面几章,我们将研究牛顿定律对较为复杂问题的应用。当世界变得更复杂时,它也就变得更有趣了,而且,我们将发现与较复杂物体的力学相联系的现象比起只是一个点来说确实要吸引人得多。当然,这些现象除了牛顿定律的组合之外并不包含其他任何东西,有时却难于使人置信,只有F =ma 在起作用。
我们研究的较为复杂物体可以分为如下几类:流动的水,旋转着的星系,等等。在开始时,要分析的最简单的“复杂”物体是所谓的刚体 ,也就是在运动时会发生转动的固体。然而,尽管是这样一个简单的物体,也可能具有非常复杂的运动。因此,首先我们将研究这种运动的最简单的形式,即一个伸展的物体绕固定轴 的转动。该物体上的某一给定点在与这根轴垂直的平面里运动。这样一种物体绕固定轴的转动称为平面转动 ,或在二维空间中的转动。以后我们将把结果推广到三维空间,但在这样做的时候我们将发现,它不像通常的质点力学那样易于推广,如果我们不首先在二维空间中打好坚实的基础,则三维空间中的转动是难于理解和难以捉摸的。
如果把一个由弦线联在一起的许多木块和木条所组成的物体抛到空中,我们就可以在这个过程中观察到第一个有趣的有关复杂物体运动的定理在起作用。当然,我们知道,如果我们研究的是一个质点,它将沿一条抛物线运动。但是,现在我们的物体不是 一个质点,它将摇摆和翻滚等。尽管如此,人们仍能看到,它还是沿抛物线运动。但究竟是什么 沿抛物线运动呢?当然不是木块边角上的点,因为它在上下翻滚;也不是木条的端点和木块或木条的中间部分。但是,确实有某个东西 沿抛物线运动,那就是有效“中心”。因而第一个关于复杂物体的定理就是要表明:存在着一个在数学上可以定义的平均位置,但不一定是物体上的一个点沿抛物线运动。这就叫做质心定理,下面就来证明这一个定理。
我们可以把任何物体都看成由大量微小的粒子,即原子所组成的,在这些粒子之间存在着各种力。用i 来表示某一个粒子的标记(它们的数目极大,比方说,i 可以大到1023 )。那么,作用在第i 个粒子上的力当然是质量乘这个粒子的加速度
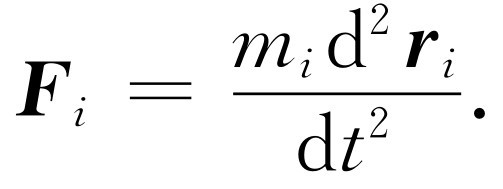 (18.1)
(18.1)
在下面几章中,运动物体的各个部分都是以远小于光速的速率运动,所以对所有的量我们将用非相对论近似。在这种情况下,质量是常数,因此
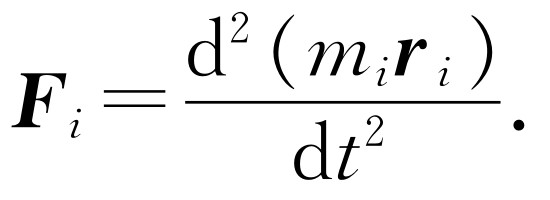 (18.2)
(18.2)
如果我们把作用在所有粒子上的力都加起来,也就是说,假如对所有不同标记的 F i 求和,我们就得到总的力 F 。在等式的另一端,我们在微分之前先相加
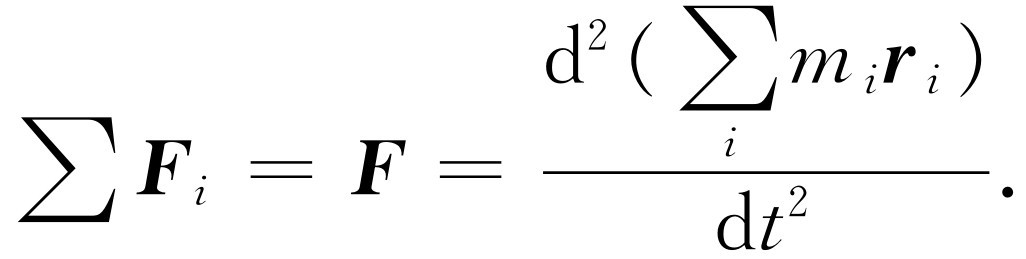 (18.3)
(18.3)
因此,总的力就等于各个质量与位置乘积之和的二阶微商。
现在作用在所有粒子上的总的力与外 力相同。为什么呢?虽然由于弦线的存在,作用在粒子上有各种各样的力,如摆动力、推力、拉力、原子力以及天知道还有什么形式的力,我们应该把所有这些力都加起来,但牛顿第三定律却帮助了我们。由于在任何两个粒子之间的作用和反作用是相等的,因而当我们把所有的方程式加起来时,如果任何两个粒子之间有力作用着,那么在求和时这些力将相互抵消。因此,最后的结果是只剩下那些来自其他粒子的作用力,这些粒子不包含在我们所要求和的那个物体里面。因此,假如式(18.3)是对一定数量的粒子求和,这些粒子一起构成了所谓“物体”,那么作用在整个物体上的外 力就等于作用在组成它的各个粒子上的所有力的和。
如果我们能够把式(18.3)写成总质量和某一个加速度的乘积,那么问题就好办多了。这是可以做到的。我们用M 来代表所有质量的总和,也就是总质量。如果我们定义 一个矢量 R 为
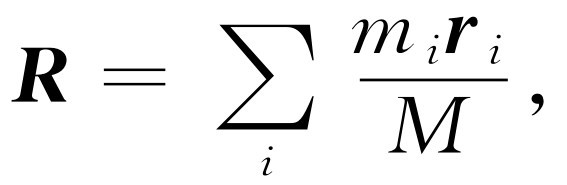 (18.4)
(18.4)
由于M 是常数,则式(18.3)将简化成
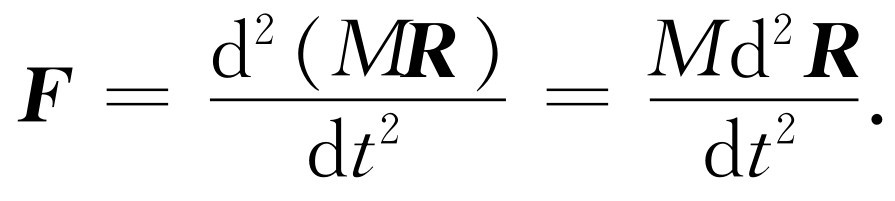 (18.5)
(18.5)
于是我们得出,外力等于总质量和某一位于 R 的假想点的加速度的乘积。这个点称为物体的质心 。它是位于物体“中间”某处的一个点,是 r 的一种平均值。在这种平均值中,各个不同的 r i 的权重(即重要性)与其质量成正比。
在下一章中我们将更详细地讨论这个定理,这里我们只限于指出两点:第一,假如外力为零,物体在真空中漂移,它可以以旋转、晃动、扭转等形式做各种运动。但是它的质心 ——这个人为地创造和计算出来、位于其中的某一位置——将以一个恒定的速度运动 。特别是,假如它原来是静止的,它将保持静止。因此,假如有某种容器,比方说载人的宇宙飞船,我们算出它的质心位置,并且发现这个质心是静止的,那么,如果没有外力作用在这个容器上,它将一直保持静止。当然,由于人在内部来回走动,宇宙飞船可以作某种微小的运动;当人向前走的时候,飞船就向后退,以保持所有质量的平均位置严格处于同一点。
那么,由于人们不能使质心运动,是不是就绝对不可能发射火箭呢?显然不是。但是,我们当然也会发现要想推动火箭中的有用部分,就要把一些无用部分抛掉。换句话说,如果开始时火箭的速度为零,我们让气体从它的尾部喷出,那么,当这股小气流向一个方向喷出时,火箭飞船就向另一个方向运动,但是它们的质心仍旧严格地处于原来的位置。因此,我们只是使有用的那部分相对于无用的另一部分作运动而已。
关于质心的第二点,也就是我们在这个时候要引进它的原因,在于质心的运动可以和物体“内部”的运动分开来处理,因此,我们在讨论转动时可以不去考虑它。
§18-2 刚体的转动
现在我们来讨论物体的转动。当然,一般物体不仅会转动,还会晃动,摇动和弯曲。为了使问题简化起见,我们将讨论一种称为刚体 ——但实际上并不存在的理想物体——的运动。刚体的意思是说这个物体的原子之间的作用力非常强,由于这种特性,使它运动所需的很小的力,不会使它发生形变。当刚体运动的时候,它的形状实质上是保持不变的。如果我们希望研究这种物体的运动,并且不去考虑它的质心的运动,那么就只剩下转动 了。我们怎样来描写转动呢?假如在物体上有一条线保持不动(它可以穿过质心,也可以不穿过),物体就以这根特殊的线为轴转动。如何来确定转动呢?这很容易,在物体上除轴线以外的任何一个地方记下一点,只要知道这个点运动到什么地方,我们就能够准确地说出物体的位置。描述这个点的位置,只要用一个角度 就够了。所以转动就是研究这个角度随时间的变化。
为了研究转动,我们来观察一个物体转过的角度。当然,我们并不是指物体本身内 部的某一特定的角度;也不是说我们在物体上 画出某一角度。我们指的是从某一时刻到另一时刻整个物体位置的角变化 。
首先,我们来研究转动运动学。角度随着时间而变化,就像我们在一维情况下讨论位置和速度那样,在平面转动中可以讨论角位置和角速度。实际上,在二维转动和一维位移之间存在着一个非常有趣的联系,几乎每一个量都有它的对应的量。首先,这里有一个确定物体转过 多远的角度θ ,它代替了确定物体移动 多远的距离y 。同样,正如在一维空间中有一个表示物体运动得多快,或者在一秒钟内走了多远的速度v =ds /dt 那样,这里也有一个表示一秒钟内角度的变化多大的转动速度,ω =dθ /dt 。假如用弧度来测量角度,那么角速度ω 就是每秒多少弧度。角速度越大,物体转动得越快,角度变化也越快。再继续下去,我们可以把角速度对时间微分,并称α =dω /dt =d2 θ /dt 2 为角加速度。它与通常的加速度相对应。
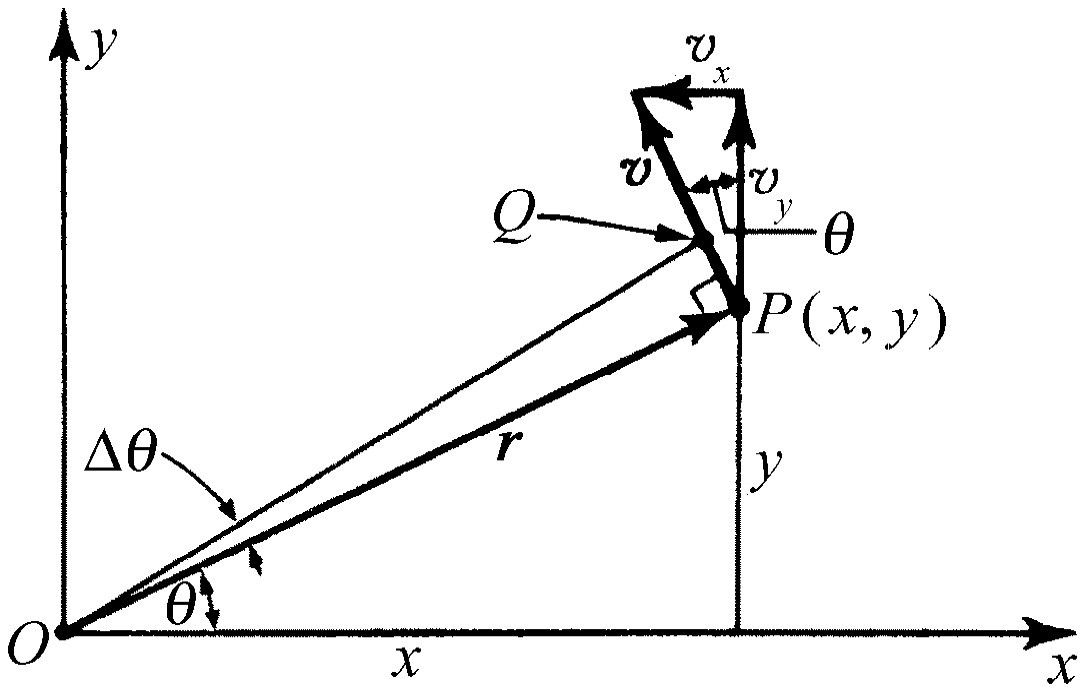
当然,我们还应该把转动动力学和构成物体的质点动力学规律联系起来,因此,我们应求出,当角速度为某一值时,某一特定质点是如何运动的。为此,通常的做法是,我们在离开轴的距离为r 处取一质点,在一给定时刻它处于某一位置P (x ,y ),如图(18.1)所示。假如经过Δt 时间后,整个物体转过Δθ 角,这个质点也和物体一起运动。它离开O 点的距离和以前一样,但被带到了Q 点。我们要知道的第一件事是它在x 方向上的距离变化了多少,在y 方向上的距离又变化了多少。令OP 为r ,那么根据角度的定义,PQ 的长度为r Δθ 。这样,x 值的变化就正好是r Δθ 在x 方向上的投影
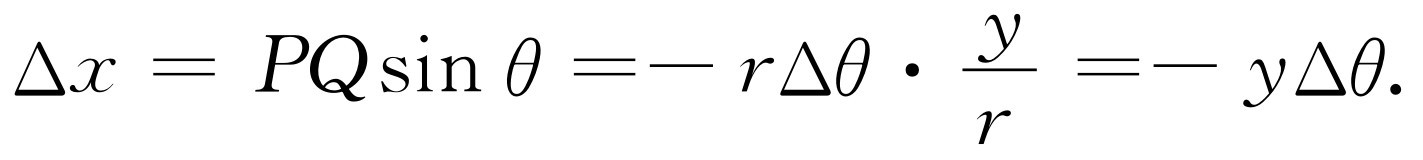 (18.6)
(18.6)
同样
Δy =+x Δθ .(18.7)
假如物体是以一个给定的角速度ω 转动,用Δt 去除式(18.6)和(18.7)的两边后,我们发现质点的速度为
v x =-ωy 和v y =+ωx .(18.8)
当然,如果要求出速度的大小,则可写成
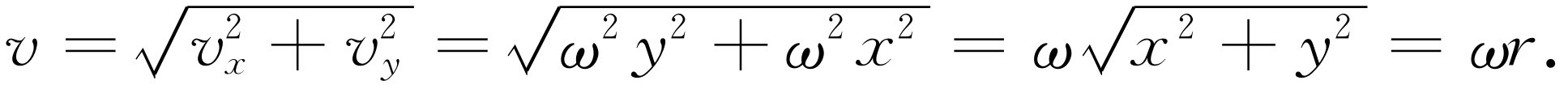 (18.9)
(18.9)
这个速度的大小为ωr ,这并不是不可思议的;实际上,这应当是不证自明的,因为它走过的距离是r Δθ ,而每秒钟走过的距离就是r Δθ /Δt ,即rω 。
现在我们转向研究转动动力学 。这里必须引进一个力 的新的概念。我们要考察一下是否能够找到某个量,它对转动的关系就像力对线性运动的关系那样,我们称它为转矩 (转矩的英文名称torque,这个字起源于拉丁文torquere,即扭转的意思)。力是产生线性运动所必须的,而要使某一物体转动就需要有一个“旋转力”或“扭转力”,即转矩。定性地说,转矩就是“扭转”;但定量地说,转矩又是什么呢?因为定义力的一个最好的办法是看在力作用下通过某一给定的位移时,它做了多少功 ,所以通过研究转动一个物体时做了多少功 就能定量地得出转矩的理论。为了保持线性运动和角运动的各个量之间的对应关系,我们让在力作用下物体转过一个微小距离时所做的功等于转矩 与物体转过的角度 的乘积。换句话说,我们是这样来定义转矩,使得功的定理对两者完全相同:力乘距离是功,转矩乘角度也是功。这就告诉了我们转矩是什么。例如,我们来考虑一个有几种不同的力同时作用在上面的刚体,它绕一根轴转动。首先,我们集中注意观察一个力,并假定这个力作用于某一点(x ,y )上。那么,如果物体转过一个很小的角度,它做了多少功呢?这很容易,所做的功是
ΔW =F x Δx +F y Δy .(18.10)
我们只要用式(18.6)和式(18.7)两者来代替Δx 和Δy 就得出
ΔW =(xF y -yF x )Δθ .(18.11)
这就是说,所做的功的大小实际上等于物体转过的角度乘上一种看上去很奇特的力和距离的组合。这个“奇特的组合”正是我们所说的转矩。由于功的变化定义为转矩乘角度,所以我们就得出了用力表示的转矩公式(显然,转矩并不是一个与牛顿力学完全无关的新的概念,转矩必须有一个明确的借助于力的定义)。
当有几个力同时作用时,当然,所做的功应等于各个力所做的功之和,因此,ΔW 将包括很多项,即把对应于所有力的各项加到一起,而每一项都与Δθ 成正比。 我们可以把Δθ 提出来,因此可以说,功的改变等于各个不同的作用力产生的所有转矩之和与Δθ 的乘积。这个和称为总转矩τ 。因而,转矩能用一般的代数规律相加,但以后会看到,这仅仅适用于在一个平面里的运动。就像在一维的动力学中,力可以用简单的代数法相加一样,但这只是因为它们都处在同一个方向上。在三维空间中情况就比较复杂。对于二维转动有
τ i =x i F yi -y i F xi (18.12)
和
τ =∑τ i .(18.13)
必须强调指出,转矩是相对于某一给定轴而言的。假如选取不同的轴,则所有的x i 和y i 都改变了,转矩的值(一般说来)也要改变。
现在我们稍微注意一下,在前面从功的概念引出转矩时,也给出了物体在平衡时的一个很重要的结果:如果作用在一个物体上的所有的力对平动和转动而言都是平衡的,则不仅净力 为零,而且总转矩也为零,因为假如一个物体处于平衡,那么对于微小的位移外力不做功 。因此既然ΔW =τ Δθ =0,则所有转矩之和也应为零。这样对平衡来说就有两个条件:力的和是零,转矩的和也是零。读者可以证明,在平衡时,必须保证绕任何一根 轴(在二维空间中)的转矩之和都为零。
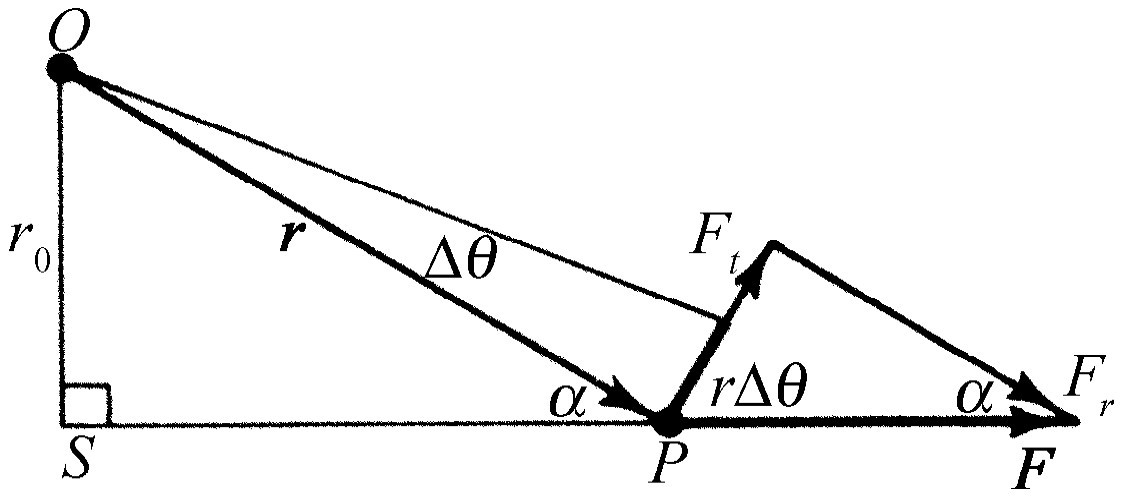
现在我们来考虑单个力,并试图用几何法来画出奇特的项xF y -yF x 。在图18-2中,我们看到一个力 F 作用在点P 上。当物体转过一个小的角度Δθ 时,所做的功应该等于力在位移方向上的分量和位移的乘积。换句话说,需要计算的只是力的切向分量和距离r Δθ 。因此,我们看到转矩也等于力的切向分量(垂直于半径)和半径的乘积。根据转矩的一般概念就能了解,假如力完全是径向的,它就不能使物体“扭转”;很明显,扭转效应仅与不是把它从中心拉出来的那部分力有关,这部分力就是切向分量。此外,显然,一个给定的力作用在长臂上要比接近轴线时效果更大。实际上,如果我们正好推在轴 上,根本不会发生扭转。因此,这就使我们了解到,扭转或转矩的大小是与径向距离和力的切向分量成正比的。
转矩还有第三个非常有趣的公式。我们刚刚在图18-2中已经看到转矩等于力乘半径再乘sin α 。但是,假如我们延长力的作用线,并画一条与力的作用线垂直的直线OS (即力臂 ),我们发现这个力臂相对于r 之比等于力的切向分量相对于总力之比。因此,转矩公式还可以写成力的大小乘力臂的长度。
转矩通常也叫力矩 。这个字的来源不很清楚,但是moment是从拉丁语中的movimentum衍生出来的,而且一个力移动物体的能力(力作用在一个杠杆或一根撬棒上)是随力臂长度的增加而增加的,因此,它的来源可能与此有关。在数学上“矩”(“moment”)的意思是用离开轴的距离多少来加权的。
§18-3 角动量
虽然到目前为止我们只考虑了刚体这一特殊情况,但是转矩的性质和它的数学关系式即使对非刚体也是有意义的。实际上,我们可以证明一个非常值得注意的定理:就像外力是一群质点的总动量p 的变化率一样,外转矩是一群质点的角动量 L 的变化率。
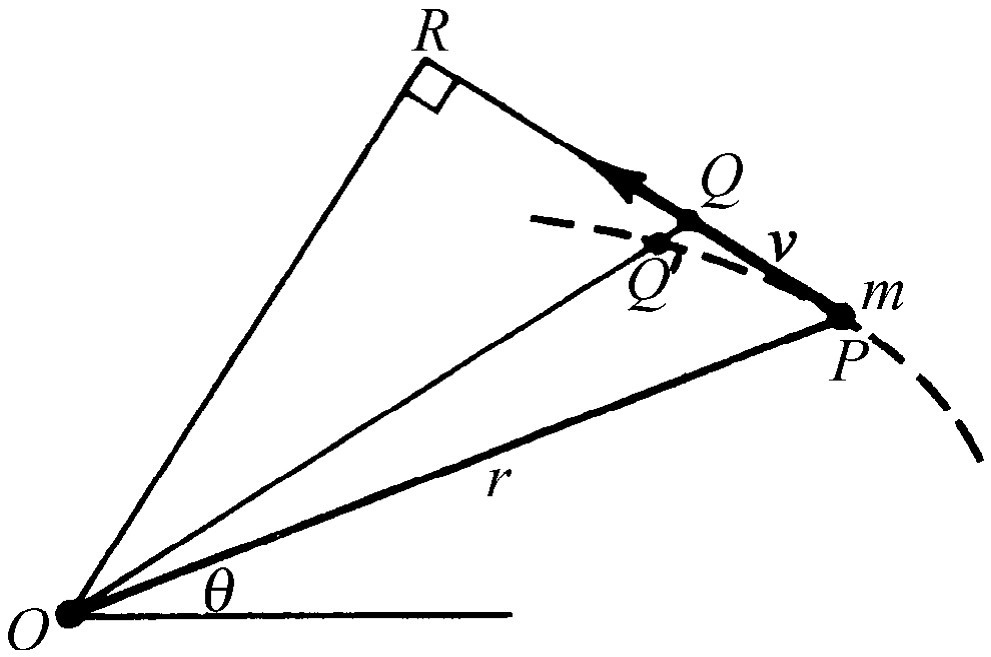
为了证明这一点,我们假设有某些力作用在一个由许多质点组成的系统上,并观察在这些力产生的转矩的作用下,系统会发生什么变化。当然,首先我们只考虑一个 质点。图18-3所示的是一个质量为m 的质点和一根轴O ;这个质点不一定绕O 作圆周运动,它可以像行星绕太阳一样沿一个椭圆运动,或者沿某个其他曲线运动,反正它在运动,而且有力作用在上面,并且按照通常的公式,即力的x 分量等于质量乘加速度x 的分量,等等。但是我们再来看一下转矩 是什么呢?转矩等于xF y -yF x ,而在x 或y 方向上的力是质量乘上在x 或y 方向上的加速度
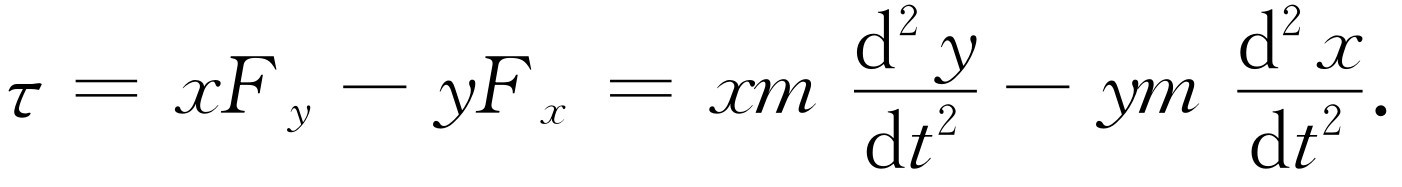 (18.14)
(18.14)
虽然,看来这个式子不是一个简单的量的微商,但实际上它是量xm (dy /dt )-ym (dx /dt )的微商
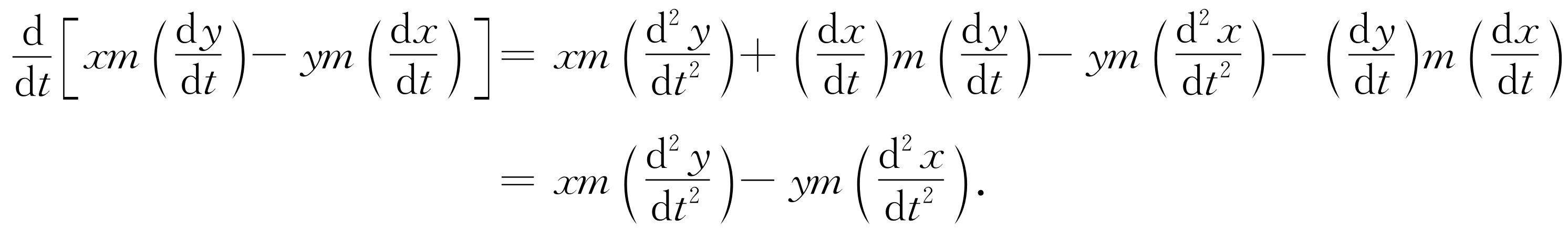 (18.15)
(18.15)
因此,转矩确实是某个量随时间的变化率,所以“某个量”引起了我们的注意,我们给它一个名称,叫角动量,并用L 来表示
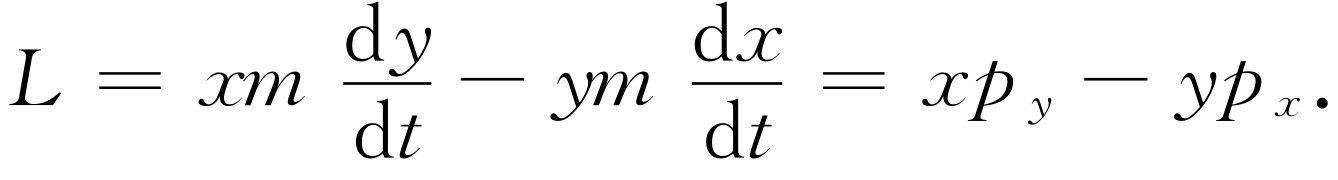 (18.16)
(18.16)
虽然,我们目前的讨论是非相对论的,但L 的第二种形式对相对论也是正确的。因此,我们发现对于动量也有一个转动的对应量,这就是角动量,它是用线动量的分量来表示的,就像转矩公式是用力的分量来表示的一样!这样,假如我们要知道一个质点相对于某一个轴的角动量,只要用动量的切向分量和半径相乘就行了。换句话说,计算角动量并不是看它离开 原点有多快,而是看它围绕 原点转动有多快。在角动量中只计及动量的切向部分。而且,动量作用线伸展得越远,角动量就越大。此外,由于不管这个量记为p 还是F ,其几何图像相同,因此,必定存在着一个动量臂(与作用在质点上的力臂不一样 ),只要延长动量 的作用线,再找出到轴的垂直距离就可以求出它。因此,角动量就是动量的大小和动量臂的乘积。像转矩有三个公式一样,角动量也有三个公式
L =xp y -yp x =rp 切向 =p ·动量臂.(18.17)
与转矩一样,角动量与所要计算的轴的位置有关。
在我们着手处理一个以上的质点问题之前,先让我们应用上面的结果来讨论行星围绕太阳旋转的问题。力在什么方向?力是指向太阳的。那么作用在物体上的转矩是什么?当然,这与我们把轴取在哪里有关。但是,因为转矩是力和力臂的乘积,或者说是力垂直于r 的分量与r 的乘积,所以如果以太阳本身作为轴,就可以得到很简单的结果。因为这时没有切向力,所以相对于在太阳处的轴的转矩为零。因此,围绕太阳转动的行星的角动量不变。我们来看看这意味着什么。速度的切向分量乘质量再乘半径将是一个常数,因为它就是角动量,而角动量的变化率是转矩,在这个问题中,转矩为零。当然,既然质量也是一个常数,这必然意味着切向速度乘半径是一个常数。对行星运动而言,这正是某种我们早已知道的结果。假设,我们考虑一个微小的时间增量Δt 。当行星从P 点运动到Q 点(图18-3)时,它将走多远?它将扫过多大的面积 ?因为面积QQ′P 与面积OPQ 相比非常小,可以略去,所以只要用基线PQ 的一半乘高OR 就可求出扫过的面积。换句话说,单位时间内所扫过的面积等于速度乘速度臂(再乘以1/2)。这就是说,面积的变化率正比于角动量,而角动量是一个常数。因此,当力产生的转矩为零时,在相等的时间内扫过相等的面积的开普勒定律正是角动量守恒定律的一种文字表述。
§18-4 角动量守恒
现在我们继续讨论当有大量质点存在以及一个物体由很多部分组成,各部分之间有很多力相互作用,同时它们还受到外力作用时,会发生什么情况?当然,我们已经知道,相对于任何一个固定轴,作用在第i 个质点上的转矩(也就是作用在第i 个质点上的力乘该力的力臂),等于这个质点的角动量的变化率,而第i 个质点的角动量就是它的动量和动量臂之积。假设我们把所有质点的转矩τ i 相加,并把它们的和称为总转矩τ ,那么这就是所有质点角动量L i 之和的变化率,L i 之和定义一个新的量,我们称它为总角动量L 。就像一个物体的总动量 是它所有各部分的动量之和一样,总角动量是所有各部分的角动量之和。于是总角动量L 的变化率就是总转矩
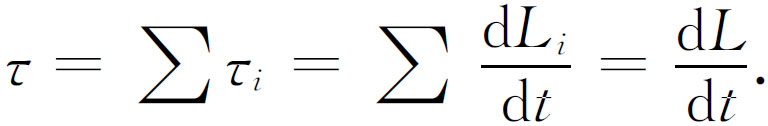 (18.18)
(18.18)
总转矩似乎是很复杂的。这里的所有内力和所有外力都必须考虑。但是,假如考虑到牛顿的作用和反作用定律,作用和反作用不仅大小相等,而且在同一条直线上 ,方向完全相反 (不管牛顿是否真正这样说过,但他确是默认了这一点),那么,在两个相互作用的物体上,因为相互作用对于任一转轴的力臂都相等,由它们产生的两个转矩 相等、方向相反。因此,内转矩成对地抵消掉,从而得出一个值得注意的定理:相对于任何轴的总角动量的变化率等于相对于该轴的外转矩!
τ =∑τ i =τ 外 =dL /dt .(18.19)
这样,关于大量质点的集合的运动,我们就有了一个十分有用的定理,它使我们研究整体运动时不需要考虑其内部的详细机制。对于任何物体的集合,不管它们是否组成刚体,这个定理都是适用的。
上述定理的一个极其重要的情况是角动量守恒定律 :如果一个质点系统不受外转矩作用时,其角动量保持不变。
一个非常重要的特例是刚体,即具有确定形状且只作转动的物体。现在来考虑一个几何大小一定,且绕一个固定轴转动的物体。在任何时刻,物体的各个部分彼此间的关系都相同。现在来求这个物体的总角动量。假如该物体中某个质点的质量为m i ,它的位置是(x i ,y i ),那么问题就是要求出这个质点的角动量,因为总角动量就是在物体中所有这些质点的角动量之和。当然,对于作圆周运动的物体来说,它的角动量等于质量乘速度再乘离开轴的距离,而速度等于角速度乘以离开轴的距离
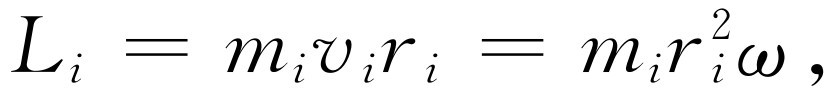 (18.20)
(18.20)
对所有的质点之求和,则得
L =Iω ,(18.21)
这里
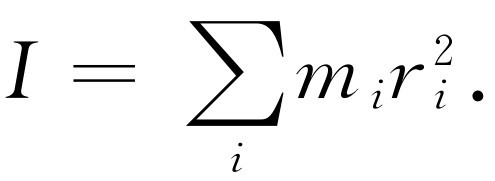 (18.22)
(18.22)
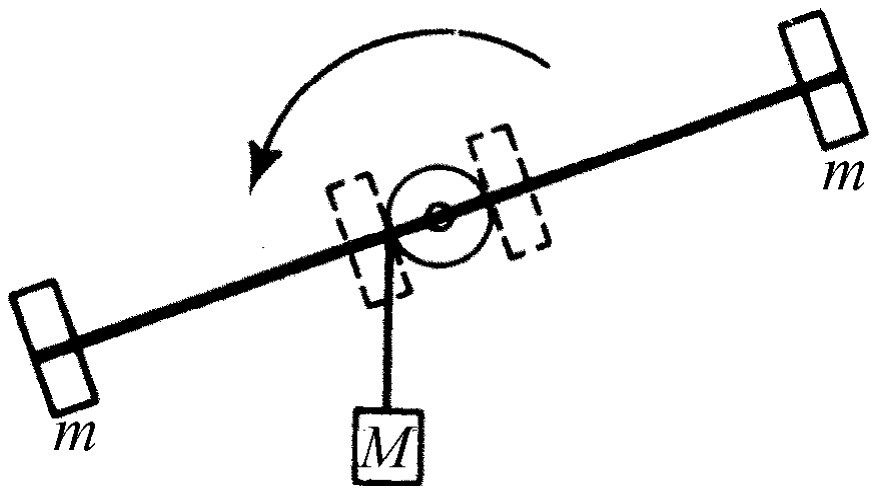
这与动量等于质量乘速度的定律相对应。速度被角速度代替,而且我们看到,质量被一个新的量所代替,这个新的量称为转动惯量I , 它与质量相当。式(18.21)和(18.22)指出一个物体所具有的转动惯量不仅与物体各质点的质量有关,还与它们离轴的距离有关 。因此,如果我们具有两个质量相同的物体,当把这两个物体放得离轴较远时,转动惯量将变大。这很容易用图18-4所示的装置来演示,在那里重物M 不能很快地落下是因为它必须转动一根有重量的长杆。首先把质量为m 的两个物体放置在靠近轴处,M 就以某一变化率加速运动。但当把这两个质量为m 的物体移到距轴较远处以改变转动惯量时,我们看到M 的加速度比先前小得多,因为这时物体阻碍转动的惯量要大得多。转动惯量是阻碍转动的惯量,它等于各个质量与它们离轴距离平方的乘积之和。
质量和转动惯量之间有一个重要的和非常引人注意的区别。物体的质量是永远不变的,而它的转动惯量可以 改变。假如我们站在一个无摩擦的转台上,把手臂伸开,并在缓慢转动时手里拿着一些重物,只要我们把手臂收拢就可以改变转动惯量,但质量并没有改变。当我们这样做时,按照角动量守恒定律,会发生各种奇妙的事情:假如外转矩为零,那么角动量,即转动惯量乘ω 将保持不变。开始时,我们以一个较大的转动惯量I 1 和较低的角速度ω 1 转动,这时的角动量为I 1 ω 1 。接着,由于把手臂收拢而使转动惯量变为一个较小的值I 2 。这样,Iω 的乘积I 2 ω 2 将保持不变,因为总角动量应该守恒。因此I 1 ω 1 =I 2 ω 2 ,这就是说,如果转动惯量减少 ,则角速度必然增大 。