第32章 辐射阻尼、光的散射
§32-1 辐射电阻
在上一章中我们知道,当一个系统振荡时,能量就被带走,我们还导出了被振荡系统所辐射掉的能量的表示式。如果知道了电场,那么电场平方的平均值乘以ε 0 c 就是每秒钟通过垂直于辐射方向的平面每平方米的能量值
S =ε 0 c 〈E 2 〉.(32.1)
任何振荡电荷都辐射能量;例如,一受激天线就辐射能量。如果系统辐射能量,则为了说明能量守恒,我们必须认为沿着通往天线的导线有功率传输着。这就是说,对驱动电路来说,天线的作用像一个电阻 或一个会“损失”能量的场所(能量并非真的损失掉,其实是辐射出去,但就电路来说,能量是损失了)。在一个普通电阻中,“损失”的能量转变成为热;在这里,所“损失”的能量跑到空间去了。但从电路理论的观点看,如果不去考虑能量跑到哪里 去了,则在电路上的净效果是同样的——能量从该电路“损失”掉了。于是对振荡器来说,天线好像有一个电阻,尽管它也许是由十分良好的铜制成的。事实上,如果天线制造得很好,它将几乎像个纯电阻,很少有电感或电容,因为我们希望从天线辐射出尽可能多的能量。这种天线所显现的电阻称为辐射电阻 。
如果流向天线的电流为I ,则传输给天线的平均功率是电流平方的平均值乘以电阻。天线所辐射 的功率当然是正比于天线中电流的平方的,因为所有的场都正比于电流,而被释放的能量正比于场的平方。辐射功率与〈I 2 〉之间的比例系数就是辐射电阻。
一个令人感兴趣的问题是,这个辐射电阻是由什么引起的?我们来举一个简单的例子:设天线中有电流被激励着上、下流动。我们发现,如果天线要辐射能量的话,必须输入功。如果取一带电体并使之上、下加速运动,它就辐射能量;如果它不带电,就不会辐射能量。从能量守恒算出能量损失是一回事,而回答反抗哪一个力 做功的问题则是另一回事。那是一个有趣而又十分困难的问题,它对于电子来说从来没有得到过完全而满意的解答,虽然对天线来说,它已解决了。情况是这样的:在天线中,由一部分天线中的运动电荷产生的场对另一部分天线中的运动电荷有作用力。我们能够算出这些力,并求出它们做了多少功,从而得到关于辐射电阻的正确规则。当我们说“我们能够算出——”时并不完全对——我们 不能,因为我们尚未学过近距离处电的规律;我们只知道远距离处的电场是什么。我们见过公式(28.3),但此刻它对我们 来说是太复杂了,不能用来计算波带区内的场。当然,因为能量守恒是成立的,我们完全可以毋须知道近距离处的场而算出结果(事实上,利用这一论证反推,最后证明只要知道远距离处的场,运用能量守恒定律,可以求出近距离处力的公式,但我们这里不去讨论这个问题)。
在单个电子的情况下,问题是如果只有一个电荷,力究竟作用在哪里?在老的经典理论中曾假定电荷是一个小球,电荷的某一部分作用于另一部分。由于此作用穿过很小电子时的延迟效应,力并不恰好与运动同相位。这就是说,如果电子静止不动,我们得到“作用力等于反作用力”。因而各个内力相等,没有净力。但是如果电子在加速运动,则由于穿过它的时间的延迟,从后面作用在前面的力就不恰好与从前面作用在后面的力相同,因为效应上有延迟的缘故。这个计时上的延迟造成了不平衡,因而,作为净效应,电子被它自己的鞋带拉住了!这个由加速度引起电阻(即运动电荷的辐射电阻)的模型遇到了很多困难,因为我们现在对电子的观点是,它不 是一个“小球”;这个问题根本没有解决。虽然如此,我们仍能正确地算出净辐射阻力应是多少,也就是当我们加速一个电荷时会有多少损耗,尽管不直接知道力如何作用的机理。
§32-2 能量辐射率
现在我们来计算加速电荷所辐射的总能量。为了使讨论不失一般性,假设电荷按非相对论性的任何方式作加速运动。比如说,当电荷加速度为竖直时,我们知道它产生的电场是电荷乘以推迟加速度的投影除以距离。因而可以知道任何一点的电场,从而知道电场的平方以及每秒钟通过单位面积的能量ε 0 cE 2 。
量ε 0 c 经常出现在与无线电波传播有关的表示式中。它的倒数称为真空阻抗 ,这是一个很容易记的数:其值为1/ ε0 c =377Ω。所以以瓦特为单位的每平方米的功率等于电场平方的平均值除以377。
应用电场表示式(29.1),我们发现
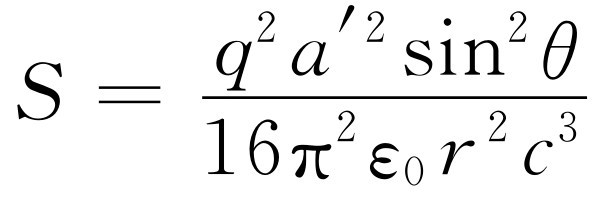 (32.2)
(32.2)
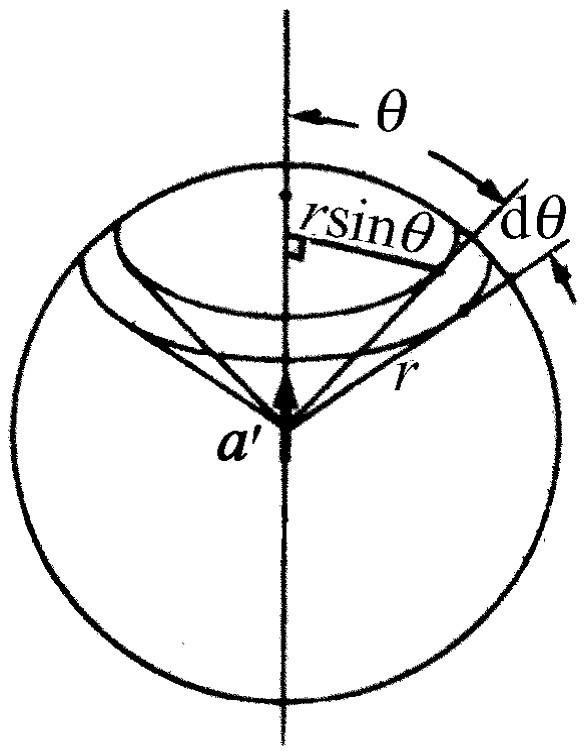
就是在θ 方向每平方米所辐射的功率。我们注意到它与距离平方成反比,如前面所说的那样。现在假如要求出向所有方向辐射的总能量,则必须将式(32.2)对所有方向积分。首先乘以面积,以求出在小角dθ 内流过的功率(图32-1)。为此要知道球面被dθ 所截部分的面积。考虑的方法是这样的:若球半径为r ,则环状球截形的宽度为r dθ ,周长为2π r sin θ ,因为r sin θ 为该圆周的半径。故这一小片球面的面积为2π r sin θ 乘以r dθ
dA =2π r 2 sin θ dθ .(32.3)
以包含在小角dθ 内的面积(以平方米为单位)乘能流[即式(32.2),每平方米的功率],即得到此方向上在θ 与θ +dθ 之间所释放的能量值;然后将它从0°到180°对θ 的所有角度积分
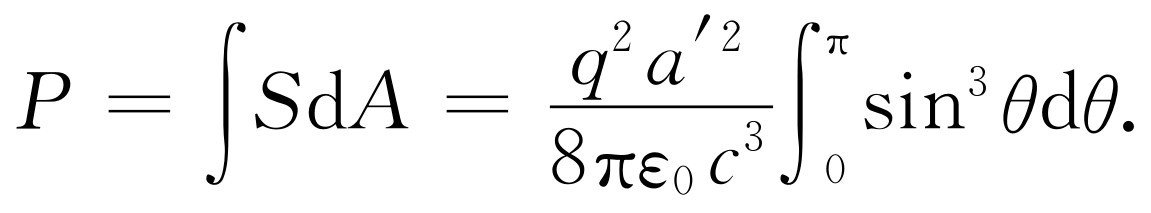 (32.4)
(32.4)
把sin3
θ
写为(1-cos2
θ
)sin θ
,不难证明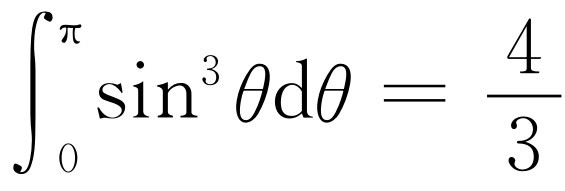 。利用这一点,最后得到
。利用这一点,最后得到
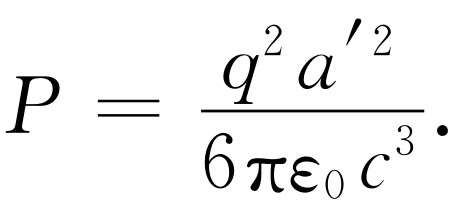 (32.5)
(32.5)
这个表示式有几点应加注意。首先,因为矢量 a ′有确定的方向,式(32.5)中的a′ 2 应为矢量 a ′的平方,即 a ′· a ′ ——矢量长度的平方。其次,能流(32.2)是用推迟加速度计算的;也就是说,用较早时刻的加速度计算,该时刻所辐射的能量现正通过球面。我们也许会说此能量事实上是在该较早时刻释放的。但这不完全正确;这只是近似的概念。能量释放的确切时间不可能精确定义。我们所能真正精确计算的只是在像一个振动或诸如此类的那样一种完整运动中所释放的能量,在那种运动里加速度最后为零。于是我们所得到的是,每周总能流为加速度平方在一个整周中的平均值。这正是在式(32.5)中所应表示出来的。或者说,如果运动的加速度在开始与末了时都为零,则流出的总能量为式(32.5)对时间的积分。
当我们有一个振动系统时,为了说明公式(32.5)的结果,我们来看一下如果电荷的位移x 在作振动,因而使加速度a 为-ω 2 x 0 e i ωt 时,情况将怎么样。加速度平方在一周中的平均值(记住,当我们对一个写为复数形式的量平方时,必须非常小心——它实在是余弦,而cos2 ωt 的平均值是1/2)从而为
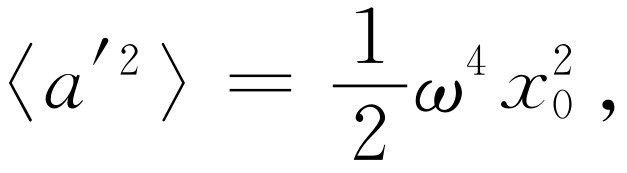
这样
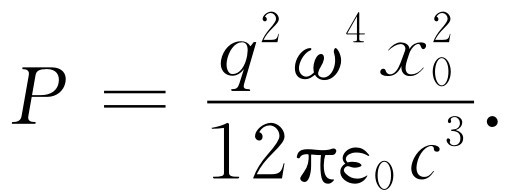 (32.6)
(32.6)
我们现在所讨论的一些公式是比较高深的,或多或少是近代的,它们最初出现于20世纪初,而且是很有名的。由于它们的历史价值,能在老一些的书中读到它们对我们来说是很重要的。实际上,老一些的书中还使用一种与我们现在的mks制不同的单位制。但所有这些复杂性在最后与电子有关的公式中可用下述规则澄清:量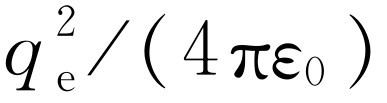 (其中q
e
是电子电荷,以库仑为单位)在历史上被写为e
2
。在mks制中很容易算出,e
在数值上等于1.518 8×10-14
,因为我们知道q
e
=1.602 06×10-19
,1/(4π
ε
0
)=8.987 48×109
。因而我们将经常使用下列方便的缩写:
(其中q
e
是电子电荷,以库仑为单位)在历史上被写为e
2
。在mks制中很容易算出,e
在数值上等于1.518 8×10-14
,因为我们知道q
e
=1.602 06×10-19
,1/(4π
ε
0
)=8.987 48×109
。因而我们将经常使用下列方便的缩写:
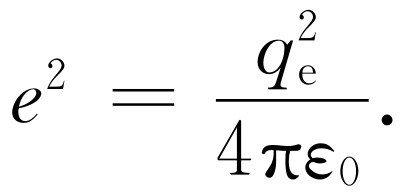 (32.7)
(32.7)
如果在老的公式中用上述数值代替e
,并把这些公式看作是用mks单位写的,就能得到正确的数值结果。例如,式(32.5)中老的形式是P
=2e
2
a
2
/(3c
3
)。再如,电子与质子在距离为r
时的势能是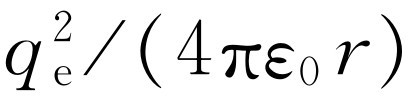 或e
2
/r
,其中e
为mks制中的值,即e
=1.518 8×10-14
。
或e
2
/r
,其中e
为mks制中的值,即e
=1.518 8×10-14
。
§32-3 辐射阻尼
振子损失一定能量的事实意味着,如果有一个电荷放在弹簧末端(或一个电子在原子中),其自然频率为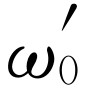 ,让它开始振动,然后放手,那么,即使它处在远离任何物体几百万里以外的真空中,它也不会永远振动下去。这里既没有通常意义上的油,也没有通常意义上的电阻;也就是没有“黏滞性”。但它仍不会像我们也许曾经说过的那样“永远”振动下去,因为当它带电时,它在辐射能量,因而振动将慢慢停止。那么慢到怎样程度?由电磁效应,即由所谓振子的辐射电阻或辐射阻尼所引起的这种振子的Q
值是多少?任何振动系统的Q
是任一时刻振子所包含的总能量除以每弧度的能量损失
,让它开始振动,然后放手,那么,即使它处在远离任何物体几百万里以外的真空中,它也不会永远振动下去。这里既没有通常意义上的油,也没有通常意义上的电阻;也就是没有“黏滞性”。但它仍不会像我们也许曾经说过的那样“永远”振动下去,因为当它带电时,它在辐射能量,因而振动将慢慢停止。那么慢到怎样程度?由电磁效应,即由所谓振子的辐射电阻或辐射阻尼所引起的这种振子的Q
值是多少?任何振动系统的Q
是任一时刻振子所包含的总能量除以每弧度的能量损失
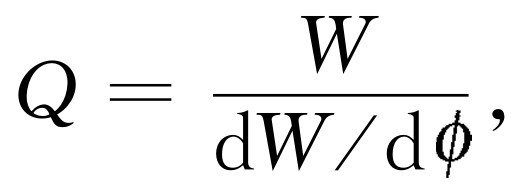
或者(另一种写法),因为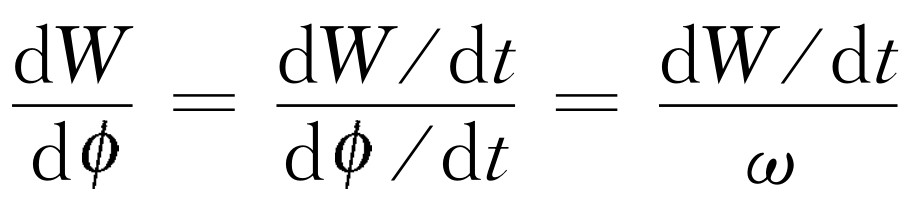 ,故
,故
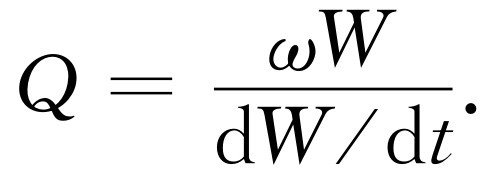 (32.8)
(32.8)
对给定的Q ,此式告诉我们振子的能量是怎样衰减的,因为dW /dt =-ωW /Q ,若W 0 为起始(t =0时)能量,则此式的解为W =W 0 e-ωt / Q 。
为了找出辐射子的Q ,我们回到式(32.8),并用式(32.6)作为dW /dt 。
那么振子的能量W
用什么?振子的动能是mv
2
/2,平均
动能就是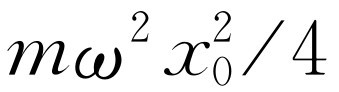 。但我们记得振子的总能量中,平均讲一半是动能,一半是势能,故将上面的结果加倍,就得到振子的总能量
。但我们记得振子的总能量中,平均讲一半是动能,一半是势能,故将上面的结果加倍,就得到振子的总能量
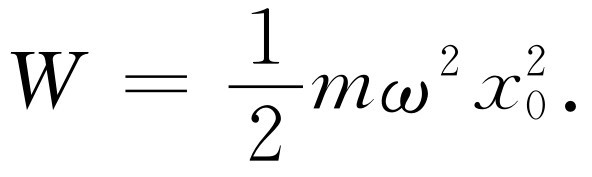 (32.9)
(32.9)
式中的频率用什么?就用自然频率ω 0 ,因为实际上,它就是原子辐射的频率,而m 就用电子质量m e 。这样,在作了必要的除法与消除后,公式变为
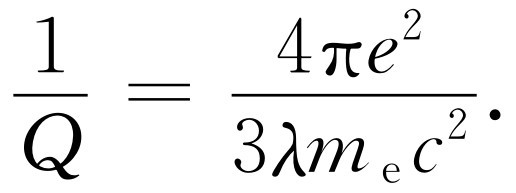 (32.10)
(32.10)
(为了更容易看清楚并迁就历史上的形式,我们用缩写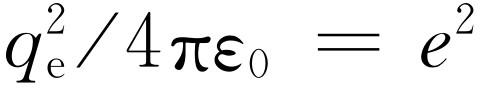 来写出此式,余下的因子ω
0
/c
已写为2π
/λ
)。因为Q
是无量纲的,组合量e
2
/m
e
c
2
必须仅仅是电子的电荷与质量的一种性质,即电子的固有特性,而且它必须是一个长度
。我们给它取了一个名字,叫电子半径
,因为被发明用来解释辐射电阻的,建立在电子的一部分对另一部分有力作用这一基础上的早期原子模型,都需要一个其线度一般为这一数量级的电子。但是,这一量现已不再表明我们相信电子确实具有
这样一个半径。在数值上,此半径大小为
来写出此式,余下的因子ω
0
/c
已写为2π
/λ
)。因为Q
是无量纲的,组合量e
2
/m
e
c
2
必须仅仅是电子的电荷与质量的一种性质,即电子的固有特性,而且它必须是一个长度
。我们给它取了一个名字,叫电子半径
,因为被发明用来解释辐射电阻的,建立在电子的一部分对另一部分有力作用这一基础上的早期原子模型,都需要一个其线度一般为这一数量级的电子。但是,这一量现已不再表明我们相信电子确实具有
这样一个半径。在数值上,此半径大小为
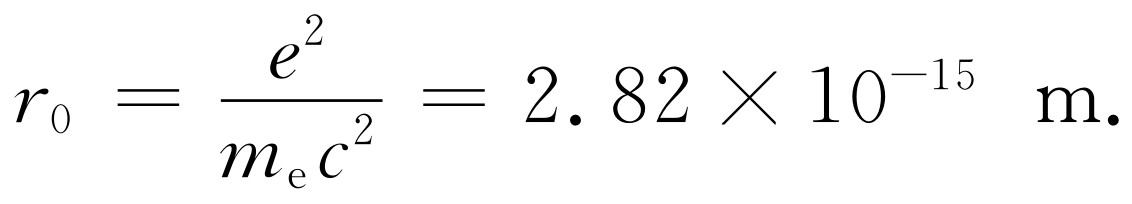 (32.11)
(32.11)
现在我们来实际计算一个发光原子——比如说Na原子的Q 。对Na原子,波长约为6 000 Å,在可见光的黄色部分,这是一个典型波长。于是
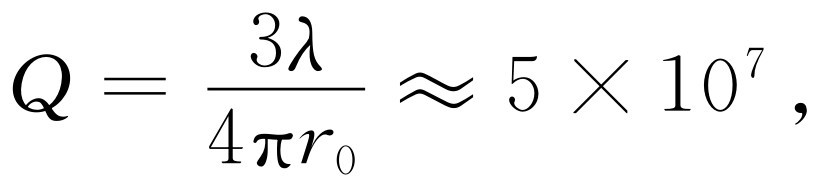 (32.12)
(32.12)
故一个原子的Q 为108 数量级。这就是说,一个原子振子在其能量降为原来的1/e 以前,将振动108 rad或约107 次。与6 000 Å对应的光的振动频率(ν =c /λ )在1015 Hz的数量级,因此寿命,即辐射原子的能量衰减为原来的1/e 所花的时间,约为10-8 s。在一般情况下,自由发光原子辐射时通常就需要这么长时间。这只对不受任何干扰的真空中的原子有效。如果电子处在固体中,则它必定要撞击别的原子或电子,从而具有附加的电阻和不同的阻尼。
振子的阻力定律中的有效阻力项γ 可以从关系1/Q =γ /ω 0 中得到,我们记得γ 的大小决定共振曲线的宽度(图23-2)。这样,我们刚才计算的就是自由辐射原子的光谱线宽度 !因为λ =2π c /ω ,我们得到
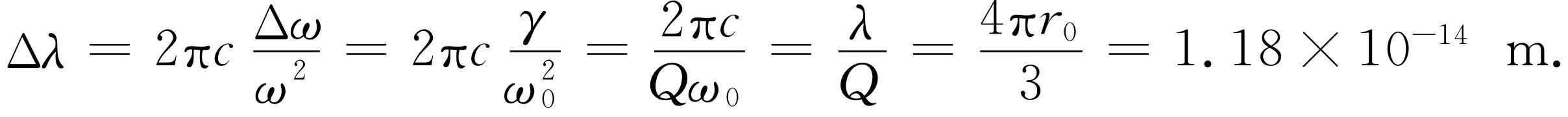 (32.13)
(32.13)
§32-4 独立的辐射源
作为本章第二个题目——光的散射的准备,我们现在必须讨论一下在以前讨论中忽略的干涉现象的某种特征。这就是什么时候干涉不 发生的问题。如果有两个源S 1 和S 2 ,振幅为A 1 和A 2 ,我们在某个方向上观察,在该方向上两个信号到达时的相位是φ 1 和φ 2 (实际振动时间与延迟时间之和所产生的相位,依观察位置而定),则接收到的能量可由合成两个复矢量A 1 和A 2 得到,一个与坐标轴成φ 1 角,另一个与坐标轴成φ 2 角(如第30章中所做的那样)。我们得到合成能量正比于
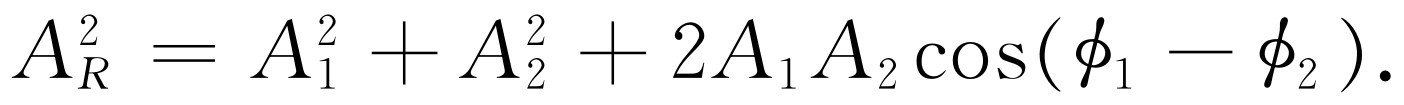 (32.14)
(32.14)
如果没有交叉项2A
1
A
2
cos(φ
1
-φ
2
),则在一给定方向上接收到的总能量将是分别由每个源所释放的能量的简单和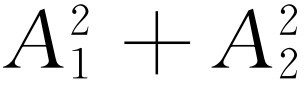 ,此即通常所预期的结果。这就是说,两个源照射在某物体上,光的合强度是两个光强度之和。另一方面,如果安排得很好,有交叉项存在,它就不是这样的和,因为还有一些干涉。如果在某些情况中,此项并不重要,则我们就说干涉表观上看来消失了。当然,实质上干涉总是存在的,只是我们不可能探测它而已。
,此即通常所预期的结果。这就是说,两个源照射在某物体上,光的合强度是两个光强度之和。另一方面,如果安排得很好,有交叉项存在,它就不是这样的和,因为还有一些干涉。如果在某些情况中,此项并不重要,则我们就说干涉表观上看来消失了。当然,实质上干涉总是存在的,只是我们不可能探测它而已。
我们来考虑几个例子。首先,假定两个源相隔7 000 000 000个波长,这不是不可能的安排。于是在给定方向相位差具有非常确定的值,这是无疑的。但是,从另一方面,只要我们沿一个方向移动一根头发丝的距离,即移动几个波长(这根本谈不上什么距离;我们的眼睛上有一个孔,它已大到使我们在观察时已在比一个波长大得多的范围内取平均效应),我们就改变了相对的相位,余弦就变化很快。如果在一个很小的观察范围内取强度的平均值 ,则余弦(它在此范围内一会儿正,一会儿负)平均得零。
所以,如果在相位随位置迅速变化的范围内取平均时,我们将得不到干涉。
举另一个例子。假定两个源是两个独立的射电振子——不是由两条导线所馈的单个振子(这种振子将保证相位保持同步),而是两个独立的源——并且它们没被精确地 调谐在相同频率(若非实际上将两个振子连接起来,要它们恰好处在同一频率是很困难的)。在这种情况下,我们有了两个所谓独立的 源。显然,既然频率不恰好相等,即使它们起始时同相位,其中之一就开始稍稍超前于另一个,一会儿它们就反相位,然后超前更多,一会儿它们又同相位。因而两个源的相位差随时间逐渐移动,但是如果我们的观察很粗糙,以致不能分辨这一小段时间,而是在比它长得多的时间内取平均,那么尽管强度具有像声音中所谓的“拍”那样的涨落,但这些涨落太快,使仪器不能跟随,于是这一项又平均掉了。
换句话说,在任何相移平均掉的情况下,我们得不到干涉!
有许多书中说两个不同的光源决不会干涉。这不是物理学的表述,而仅是写书时实验技术灵敏度的表述。光源中所发生的情况是,一个原子先辐射,接着另一个原子辐射,等等,我们只看到原子辐射一列波的时间仅持续约10-8 s;10-8 s后,某个原子接下去辐射,接着另一个原子又辐射,等等。因而相位只能在约10-8 s内保持不变。于是,如果我们在远比10-8 s长的时间内取平均,就看不到来自两个不同源的干涉,因为比10-8 s更长时,它们不能保持相位恒定。用光电池可以进行高速的探测,因而人们能够证明在10-8 s内存在着随时间上、下变化的干涉。但大多数探测装置显然不能看到这样微小的时间间隔,因而看不到干涉。当然用具有十分之一秒平均时间的眼睛是无论如何也看不到两个不同的普通光源之间的干涉的。
最近已有可能制造一种光源,它使所有原子同时 发光,从而克服了上述效应。具有这种作用的器件是一种很复杂的东西,必须用量子力学方法才能理解它。人们称它为激光 ,从激光可以产生一种光源,其干涉频率或相位保持恒定的时间远大于10-8 s。它可以是10-2 s,0.1 s甚至1 s的数量级,因而用普通光电池,人们就能够探测到两个不同的激光之间的拍频。人们很容易探测到两个激光源之间的拍的脉动。无疑不久将有人能演示这样的实验,把两个光源照射在墙上,它们的拍是这样慢,以致人们能够看见 墙在明暗变化!
另一个干涉被平均掉的情况是,不是只有两个
源,而是有许多
个源。在这种情况下,要将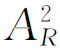 的表示式写成很多个复数振幅之和的平方,于是将得到每一项的平方的和,再加上每一对之间的交叉项,如果情况是使得后者平均掉,则将没有干涉效应。这种情况可以是这样,即各个源被置于杂乱无章的位置上,以致虽然A
2
与A
3
之间的相位差还是确定的,但它跟A
1
与A
2
等等之间的相位差很不同。因而我们将得到很多余弦项,有些为正,有些为负,加在一起平均掉了。
的表示式写成很多个复数振幅之和的平方,于是将得到每一项的平方的和,再加上每一对之间的交叉项,如果情况是使得后者平均掉,则将没有干涉效应。这种情况可以是这样,即各个源被置于杂乱无章的位置上,以致虽然A
2
与A
3
之间的相位差还是确定的,但它跟A
1
与A
2
等等之间的相位差很不同。因而我们将得到很多余弦项,有些为正,有些为负,加在一起平均掉了。
所以在许多情况下,我们看不到干涉效应,而只看到等于所有强度之和的合成的总强度。
§32-5 光的散射
上述讨论导致一种发生在空气中的效应,它是各原子的位置不规则所造成的结果。在讨论折射率时,我们曾看到入射光束使原子再辐射。入射光束的电场驱使电子上下运动,而电子由于有加速度而辐射。这些散射辐射合起来形成一个与入射光束同方向的光束,但相位略有不同,而这正是折射率的起源。
但对于在其他方向上的再辐射光的大小,我们将说些什么呢?通常,如果原子整齐地排列成有规则的花样,容易证明在其他方向得不到光,因为我们所叠加的是相位不断在变化的许多矢量,结果得零。但是如果原子杂乱地 排列,则任一方向上的总强度为每个原子所散射的强度之和 ,正如我们刚才讨论过的。而且,气体中的原子实际上在运动,所以即使此刻两个原子的相对相位有一确定的值,但不久其相位会变得很不同,从而每个 余弦项将平均掉。因此,要找出在给定方向上气体散射光的强度,只要研究一个原子 散射的效应,再将其辐射强度乘以原子数就行。
以前,我们曾说这种性质的光的散射现象是天空呈现蓝色的起因。太阳光穿过空气,当我们朝太阳的一边——比如说与光束成90°方向上——观察时将看见蓝光;现在要计算的是,我们看见多少 光以及它为什么是蓝色的 。
如果在原子所在处,入射光束的电场 E = E 0 ei ω t ,我们知道原子中的电子将由于此电场 E 而作上、下振动(图32-2)。由式(23.8),其振动幅度将是
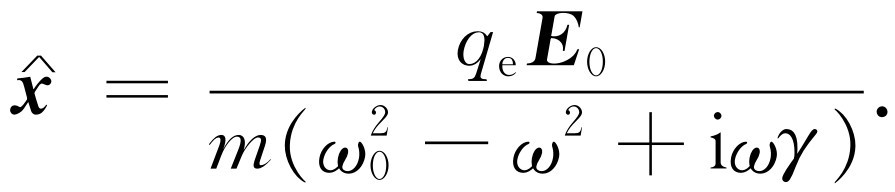 (32.15)
(32.15)
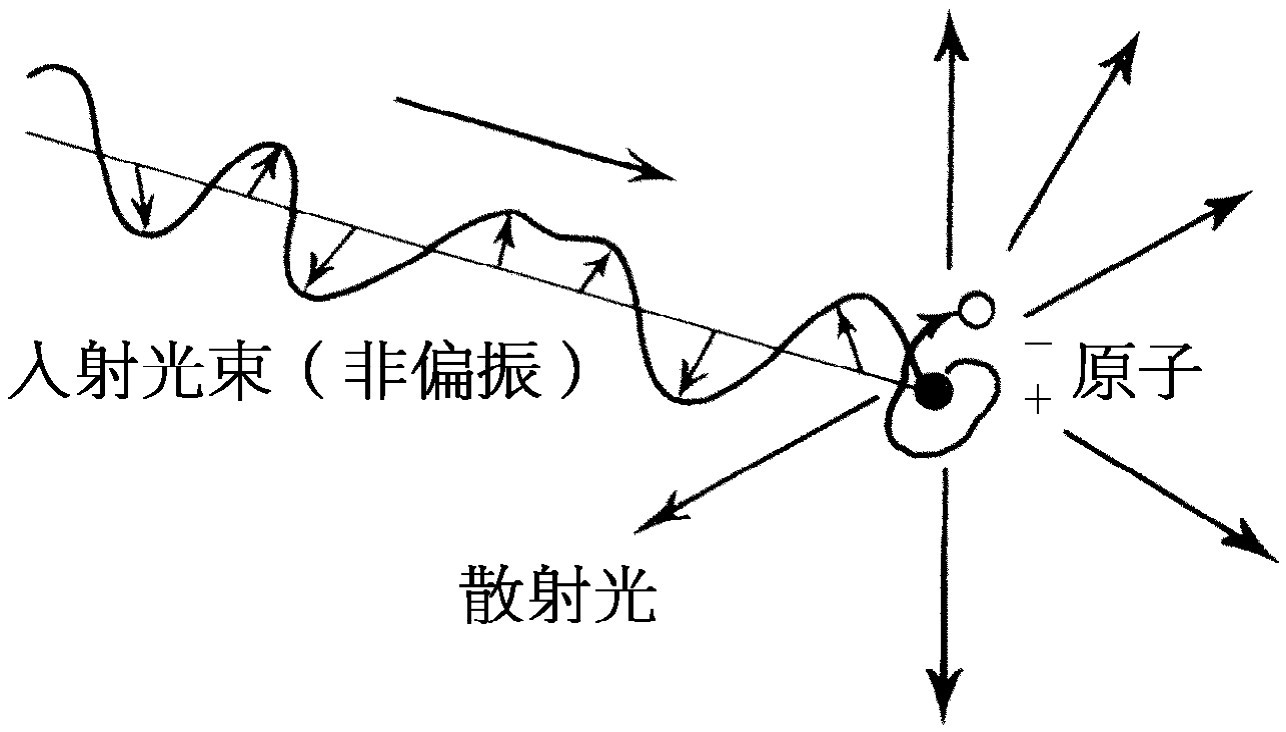
图32-2 一束光射在原子上引起原子中的电荷(电子)运动。此运动电子接着又在各个方向上辐射光
我们本来可以把阻尼以及原子表现为具有不同频率的几个振子的可能性也包括进去,并对各个频率求和,但为简单起见,我们只取一种振子,并忽略阻尼。于是对于外电场的响应(该式我们在计算折射率时已用过)就是
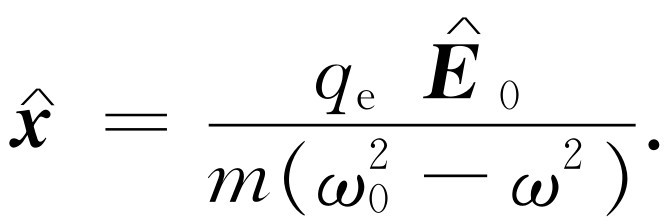 (32.16)
(32.16)
利用式(32.2)及与上述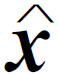 相对应的加速度,我们现在可以很容易地计算出在各个方向上发射的光的强度。
相对应的加速度,我们现在可以很容易地计算出在各个方向上发射的光的强度。
然而为了节省时间,我们不这样做,而是径直计算在所有 方向散射的光的总量 。单个原子每秒在所有方向散射的光能量的总量显然由式(32.6)给出。所以,把各部分写在一起并加以整理,得到在所有方向上辐射的总散射功率为
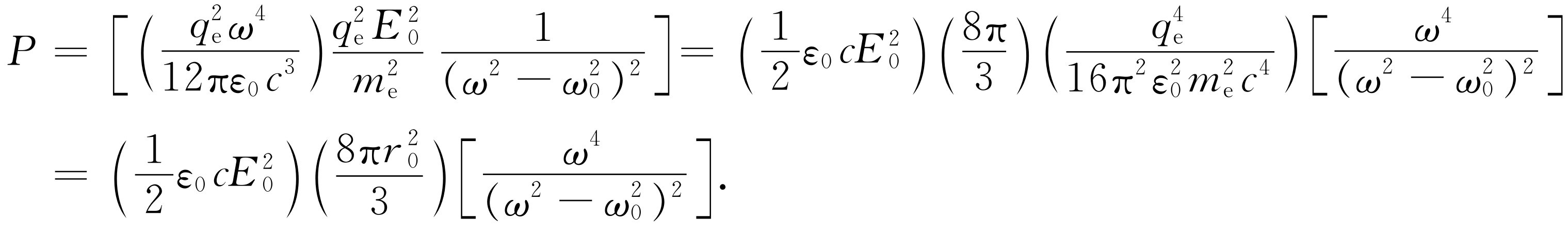 (32.17)
(32.17)
我们将结果写成上列形式,因为这样容易记:首先,散射的总能量正比于入射场的平方。这意味着什么?显然,入射场的平方正比于每秒进入的能量。事实上,每平方米每秒入射的能量是ε
0
c
乘以电场平方的平均值〈E
2
〉,而若E
0
是E
的最大值,则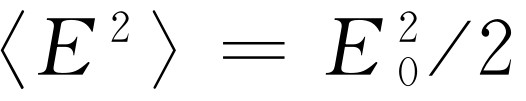 ,换句话说,散射的总能量正比于每平方米进入的能量;照射在天空上的太阳光越亮,天空看起来也将越亮。
,换句话说,散射的总能量正比于每平方米进入的能量;照射在天空上的太阳光越亮,天空看起来也将越亮。
其次,入射光散射的比例 是多少?试在光束中想象一个具有一定面积(比如说σ )的“靶”(并非实际的物质的靶,因为这会引起光的衍射等等;我们的意思是指在空间画出的一块想象的面积)。在给定条件下,通过此表面σ 的能量总量与入射强度和σ 都成正比,而有
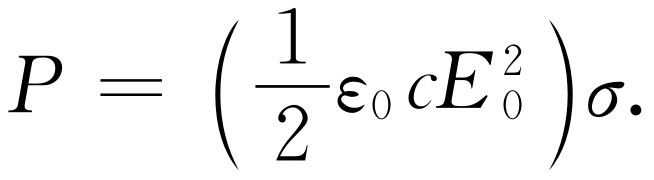 (32.18)
(32.18)
现在我们来建立一种概念:设原子散射的总强度是落在某一几何面积上的全部强度,于是只要求出该面积,就给出了答案。这样,该答案与入射强度无关;它给出了散射能量与每平方米入射能量的比率。换句话说,比率

是面积 。此面积的意义是,如果射到该面积上的所有能量被射向所有方向,则它就是被原子散射的能量的值。
这个面积称为散射截面 ;散射截面的概念是常用的,只要某一现象与光束的强度成正比。在这种情况下,人们常常这样来描述现象的强度,即说明为了收集那么多光束,有效面积必须是多少。这无论如何不是意味着此振子实际上具有 这样一个面积。如果除了一个作上、下振动的自由电子外再也不存在别的什么,在物理上就不会有与之直接相联系的面积。它仅仅是表述某种类型问题的答案的一种方法;它告诉我们为了说明有这么一些能量散射掉,入射光束所碰到的面积必须是多少。这样,对我们的情形,有
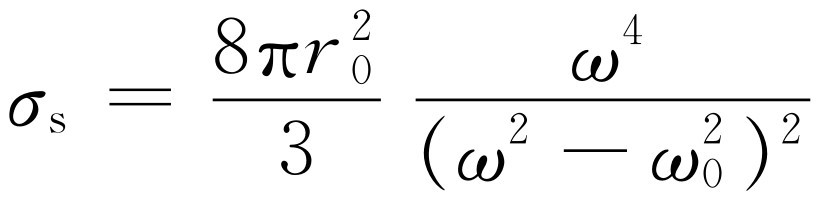 (32.19)
(32.19)
(下标s是指“散射”)。
我们来看一些例子。首先,讨论固有频率ω 0 很低的情形,或讨论完全无束缚的电子,对它来说ω 0 =0,则频率ω 消去了,截面是一常数。此低频极限或自由电子截面,称为汤姆孙散射截面 。它是每边线度约为10-15 m上下的面积,即10-30 m2 ,那是相当小的!
其次,我们讨论光在空气中的情况。我们记得空气振子的固有频率比我们所用的光的频率高得多。这意味着,作为一级近似,我们可以略去分母中的ω 2 ,于是得到散射正比于频率的四次方 。这就是说,若光的频率提高两倍,其散射强度就大16倍 ,这个差别是十分大的。这意味着蓝光(它具有比光谱红端约高两倍的频率)散射得比红光多得多。因而当我们仰望天空时,它呈现出我们经常所见的那种蔚蓝色!
对于上述结果尚需说明几点。一个有趣的问题是,为什么我们看得见云 ?云是从哪里来的?人人都知道它是水蒸气凝聚而成的。但是,水蒸气显然在凝聚以前 就已存在于大气中了,那么我们为什么看不见它呢?只在凝聚以后,它才成为完全可见的。它本来不在那里,现在却在 那里了。因而云从哪里来的奥秘其实并不是像“水是从哪里来的,爸爸?”这样的孩子提问式的奥秘那样,而是须加解释的。
我们刚才指出每个原子都散射光,当然水蒸气也散射光,奥秘在于为什么当水凝聚成云时,它散射这么大量 的光?
试考虑如果不是只有一个原子,而是有一个原子团,比如说有两个原子,彼此相对光的波长来说靠得很近,这时将发生什么。别忘了,原子直径只有1 Å左右,而光的波长约5 000 Å,所以当它们形成块,即当几个原子在一起时,相对波长来说它们可以是 靠得很近。那么当电场作用在上面时,两个原子将一起运动 。从而散射的电场将是两个同相位的电场之和,即单个原子所具有的幅度的两倍,于是散射的能量 是单个原子所散射的四倍 ,而不是两倍!所以原子团比它们成单个原子形状时散射或辐射更多的能量。我们关于相位彼此独立的论证是建立在任意两个原子间具有真正的、巨大的相位差的假设基础上的,这只有当它们相隔几个波长而且杂乱排列或在运动时才是对的。如果原子彼此紧靠着,它们必定同相位地散射光,因而它们具有相干的干涉效应,使散射增加。
如果在块团中有N 个原子,它相当于一个微小水滴,则每个原子将按与上面大致相同的方式受电场驱动(一个原子对另一个原子的影响是不重要的,因为反正对于这个问题只要有一个概念就行了),而从每个原子上散射的幅度是相同的,所以散射的总场增大了N 倍。于是散射光的强度 增大了平方倍,即N 2 倍。如果原子散开在空间,我们预期会得到N 倍,而现在却得到了N 2 倍!这就是说,N 个分子组成的水的块团中,每个分子的散射都比单个原子的散射强N 倍。所以当水凝结时,散射增大了。那么,它会无限制地 增大下去吗?不会!什么时候这种分析开始失效?我们最多可以聚集多少原子而仍可应用这个论证?答案 是:当水滴大到从一端到另一端达一个波长左右时,原子辐射就不再都同相位了,因为这时原子相隔太远。所以当我们不断增大水滴的线度时,得到越来越大的散射,直到水滴的线度达到约一个波长,在这以后散射的增大就完全不像水滴增大那么快了。而且,蓝色消失了,因为对长波长来说,在达到这一极限以前的水滴可以比短波长的更大一些。虽然对每个原子来说,短波散射得比长波多,但当所有的水滴都比波长大时,光谱红端增长得比蓝端更多一些,所以颜色从蓝色向红色移动。
现在我们可以做一个实验来演示这一点。我们可以使粒子在开始时很小,然后线度逐渐增大。我们使用硫代硫酸钠(海波)的硫酸溶液,它能够沉淀很小的硫粒子。当硫沉淀时,开始粒子很小,散射光略带蓝色。当沉淀增多时,散射光增强,当粒子变大时遂成白色。此外,直接穿过溶液的光将缺少蓝色。这正是落日为什么呈红色的原因,当然,因为光穿过空气,到达眼睛时已有许多蓝光被散射掉,所以呈火红色。
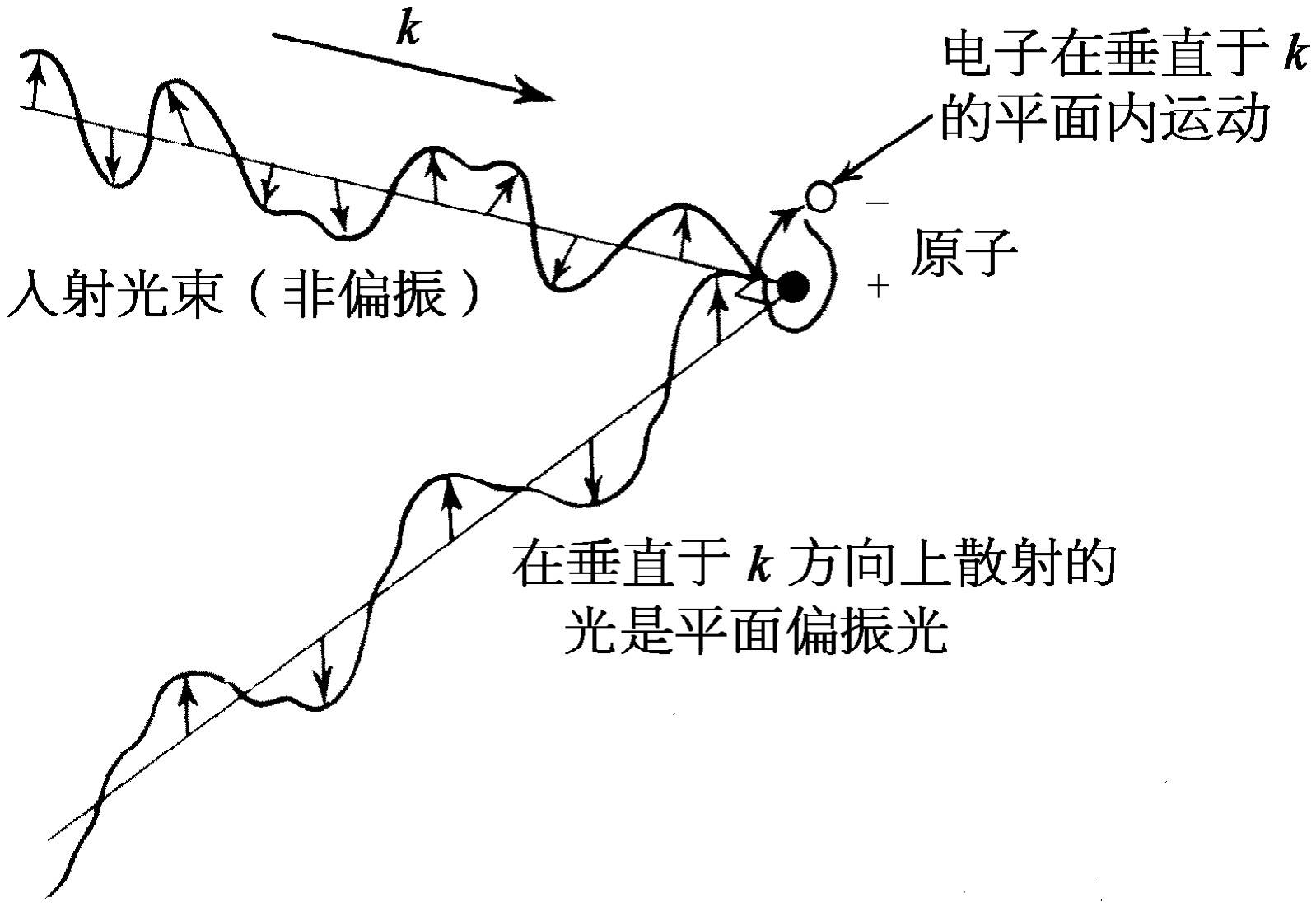
最后,还有一个关于偏振的重要特性,它其实属于下一章的内容,但因很有趣,不妨现在就提出来。这就是散射光的电场趋向于沿一个特殊方向振动的性质。入射光的电场沿某一方向振动,因而受激振子沿着与此相同的方向振动,如果我们位于与入射光束垂直的位置上,就会看到偏振 光,即其电场仅沿一个方向振动的光。一般地说,原子可以沿与入射光束垂直的任一方向振动,但是如果它们受到激发而朝着我们或背离我们振动,我们就看不见它们所发的光。所以如果入射光的电场沿任一方向振动或变化(这种光称为非偏振光),则与入射光束成90°方向出来的散射光仅沿一个方向振动!(见图32-3)
有一种称为偏振片的东西,它具有这样的性质:当光通过时,只有沿一特殊轴的电场成分可以通过。我们可以用它来检验偏振化,从而果真发现由海波溶液所散射的光是强烈偏振的。