现在来考虑一种力,它也像引力那样与距离平方成反比地变化,但比引力要强约一万亿亿亿亿 倍。另外,还有一个区别,即存在两种我们可称之为正的和负的“物质”,种类相同的相斥,不同的相吸。这就不像引力,那里只存在吸引。这样,会出现什么情景呢?
一堆正的物质会以巨力互相排斥,并向四面八方散开,一堆负的物质亦是如此。但一堆正、负物质的均匀混合物就完全不同了。相反的物质会以巨大的吸引力互相拉挽着,净结果将把那些可怕的斥力差不多完全抵消了,这是通过形成紧密而精致的正、负物质的混合体而达到的,而这样两堆分开着的混合体之间实际上就不再存在任何引力或斥力了。
确实存在这样一种力——电力。世间万物都是由此种巨力互相吸引和排斥着的正的质子与负的电子所组成的混合物。然而,平衡竟是那么完善,以致当你站在别人旁边时也根本没有任何受力的感觉。这时,即使只有一点点不平衡,你都会觉察到。例如,要是你站在别人旁边相距只有一臂之遥,而且各自都具有比本身的质子仅多出百分之一 的电子,那两人间的排斥力就会大得不得了!多大呢?足以举起那座帝国大厦 [1] ?不!举起珠穆朗玛峰?不!这个斥力应足以举起相当于整个地球的“重量”!
由于在这种致密混合物中这些巨力完善地达到了平衡,所以我们就不难理解:当物质试图保持其正、负电荷最细致的平衡时,它能具有多大的硬度与强度。例如,帝国大厦在风中之所以摇摆小于一英寸,是因为电力把每一个电子与质子或多或少地保持在其适当位置上。另一方面,如果我们在一个足够小的尺度范围内观察物质,使得只能看到几个原子,那么任一小部分就往往不会有相等数目的正电荷和负电荷,从而会存在强大的剩余电力。即使在相邻两小部分中两种电荷的数目相等,也仍然有可能拥有巨大的净电力,因为各电荷之间的力是与距离的平方成反比的。如果一部分中的负电荷,与另一部分中的正电荷靠得较近、而与负电荷离得较远,则净力就会产生。因此,吸引力可能大于排斥力,从而在两个不带额外电荷的小块中就有一个净吸引力存在。那种把各原子结合在一起的力,以及把各分子保持在一起的化学力,其实都是电力,它们在电荷的平衡不够完善、或在距离十分微小的那些区域里才起作用。
当然,你会知道,原子是由位于其核内的正的质子和核外的负电子所构成的。你也许会问:“如果这种电力那么厉害,为什么质子和电子不会正好一个紧挨着一个呢?如果它们想要形成一个紧密的混合体,为什么不会更紧密些呢?”这问题必须用量子效应来回答。要是试图把电子限制在一个很接近于质子的区域中,那么按照不确定性原理它们就得拥有一个均方动量,若我们把它们限制得越紧,这个均方动量就越大。正是这一种由量子力学规律所支配的运动,才使得电的吸引力不会把这两个电荷移得更接近些。
还有一个问题。在原子核内有若干个质子,它们全都带着正电荷,为什么它们不会互相推开呢?“是什么东西把它们结合在一起的呢?”事实是,在原子核内部,除了电力之外还存在一种称为核力的非电力,它比电力还要大,因而尽管有电的排斥力,它仍然能够把那些质子维持在一起。然而,核力是短程力——该力下降得比1/r2 急剧得多。这就产生了一个重要后果:如果一个核所含质子过多,则该核就变得太大,它便不会持久维持。铀就是这么一个例子,它含有92个质子。核力主要在每个质子(或中子)与其最近邻质子(或中子)之间起作用,而电力则在较大的距离范围内起作用,使每个质子与核内所有其他质子之间都具有排斥力。在一个核内质子的数目越多,这电的排斥作用就越强,直到铀那种情况,平衡是那么脆弱,以致于排斥性电力使得核几乎就要飞散了。这么一个核,如果稍微“轻轻敲”一下(就像曾经送进一个慢中子那样),则它就会破裂成各带有正电荷的两片,而这些裂片由于电的排斥力而飞散开去。释放出来的能量就是原子弹的能量。这种能量通常称为“核”能,但实际上却是当电力克服了吸引性核力时所释放出来的“电”能。
最后,我们还可能会问,是什么东西把带负电的电子保持在一起呢(因为它没有核力)?如果电子全都是由一种物质构成的,那它的每一部分理应排斥其他各部分,但又为什么不会飞散呢?不过,电子是否还含有“各部分”?也许,我们应该说电子只是一个点,而电力只是在不同的 点电荷之间起作用,以致电子不会作用于其本身。或许是这样吧。关于电子由什么东西束缚在一起,我们只能说到这里。这个问题对于试图建立一套完整的电磁学理论产生了不少困难,而且至今没有做出解答。我们将在以后某些章节中对这一课题多做些讨论,以为我们大家助兴。
正如我们已经见到的那样,应该指望电力与量子力学效应相结合来确定整块材料的细致结构,从而确定它们的特性。有的材料硬,有的材料软。有的是电的“导体”——因为它们中的电子能够自由运动;其他则是“绝缘体”——因为其中的电子被牢固地束缚在各个原子内。这些性质是如何得来的?那是一个十分复杂的课题,我们将在以后加以讨论。因而现在仅就一些简单情况下的电力进行考察,也就是说,现在着手处理电方面——也包括磁方面(那实际上是同一课题的另一个部分)——的规律。
我们曾经说过,和引力相似,电力与电荷间距离的平方成反比地减弱,这一关系叫作库仑定律。但当电荷运动时,这一定律就不完全准确——电力也以一种复杂的方式依赖于电荷的运动。运动电荷之间的作用力,有一部分我们称之为磁 力,事实上,它是电效应的一个方面。这也是为什么要把这一课题叫作“电磁学”的缘故。
由于存在着一个重要的普遍原理,因而有可能以相对简单的方式来处理电磁力。我们从实验发现,作用于某一特定电荷上的力——不管其他电荷的数量和运动方式如何——只取决于该特定电荷的位置、速度以及所带的电荷量。我们可把作用于一个以速度v运动的电荷q上的力F写成:
F=q(E+v×B). (1.1)
式中E和B分别叫做电荷所在处的电场 和磁场 。重要的是,来自宇宙中所有其他电荷的力都可用刚才给出的这两个矢量叠加而成。它们的值将取决于这一电荷位于何处 ,并且可能随时间 而改变。此外,如果我们用另一个电荷来代替该电荷,只要世界上所有其他电荷都不改变其位置和运动,则作用于这一新电荷上的力恰好与其电荷量成正比。当然,在实际情况中,每一电荷对邻近的所有其他电荷都产生力,从而可能引起这些电荷运动。所以在某些情况下,如果我们用另一个电荷来代替该特定电荷,则场可能 改变。
我们从第1卷已经懂得若知道了作用在一个质点上的力,应怎样去求出该质点的运动。可以把式(1.1)和运动方程相结合而得出:
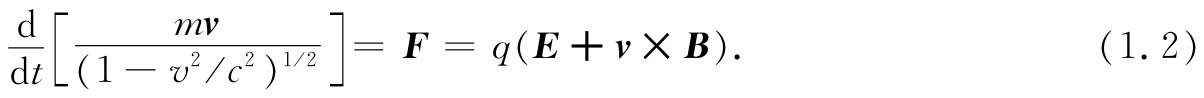
因此若E和B已知,则可以求得运动。现在我们需要弄清楚E和B是怎样产生的。
关于电磁场产生方法最重要的简化原理之一是:假设若干个以某种方式运动的电荷产生一个场E1 ,而另一组电荷产生场E2 ,而这两组电荷同时被置于原来的位置(保持它们被分别考虑时具有的相同的位置和相同的运动),那么所产生的场恰好是两个场的和,即
E=E1 +E2 . (1.3)
这一个事实称为场的叠加原理 。这原理也适用于磁场。
这一原理意味着,如果知道了关于以任意方式运动的单个 电荷所产生的电场和磁场的规律,那么所有电动力学的规律就告齐全了。如果我们想要知道作用于电荷A上的力,就只需算出由B,C,D等各电荷所产生的E和B,然后把所有电荷产生的E和B分别相加而求得总场,再从这两个总场求得作用于电荷A的力。只要结果证明,由单个电荷产生的场很简单,那么这就是描写电动力学规律的最简洁方法。可惜,我们已给出了这一定律的描述(第1卷第28章),那是相当复杂的。
事实证明,电动力学规律在其中最为简单的那一种形式,并非是人们可以期望的。要写出一个电荷对另一个电荷所产生的力的公式,并非那么容易。的确,当电荷静止不动时,库仑力的定律是十分简单的。但当电荷运动时,由于时间上的延迟和加速度的影响以及其他一些缘故,关系就变得复杂了。因此,我们并不希望仅仅凭作用于各电荷间的力的规律来介绍电动力学;而发现更方便的是去考虑另一个观点——那是电动力学规律表现得最易于处理的一种观点。