矢量场在数学上有两个重要性质,我们将利用它们从场的观点来描述电学定律。若我们想象某种闭合面,并试问是否有“某种东西”从里面流失;这就是说,该场是否有一个“流出”的量?例如,对于速度场,我们也许要问,该面上的速度是否总是向外,或更普遍地问,是否(每单位时间)流出的流体比流入的多。我们把单位时间流经该面的净流体量称为通过该面的“速度通量”。流经一个面积单元的流量恰好等于垂直该面积的速度分量乘以该面积。对于任一个闭合面,净流出量 (或通量 )等于速度向外的法向分量的平均值乘以该闭合曲面的面积:
通量=(平均法向分量)·(曲面的面积). (1.4)
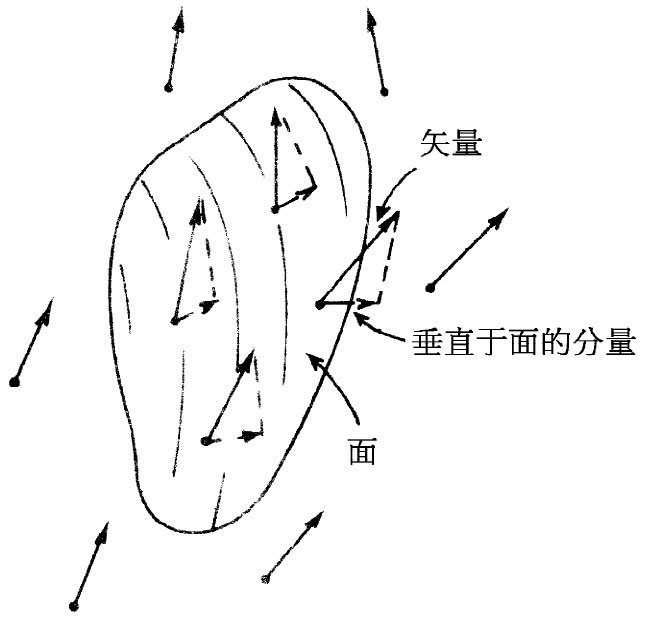
在电场的情况下,我们可以在数学上定义与流出量相类似的东西,又称作通量,但这当然不是任何物质的流动,因为电场并不是任何东西的速度。然而,事实证明,场法向分量的平均值这个数学上的量仍有其实用意义。于是,我们来谈谈电通量 ——这也是由式(1.4)定义的。最后,不仅谈论通过一个完全闭合曲面的通量,而且还谈论通过任一个有边界的曲面的通量,这也是很有用处的。综上所述,通过这样一个面的通量被定义为矢量的法向分量的平均值乘以该曲面的面积。这些概念如图1-3所示。

图1-3 矢量场通过一个曲面的通量,定义为矢量的法向分量的平均值乘以该曲面的面积
矢量场还有第二个性质,它必须用一条曲线而不是用一个面才能得出。让我们再来回顾一下描写液体流动的速度场,也许会提出这样一个有趣的问题:该液体是否存在环流?我们所说的环流,是指是否有围绕某个环路的净旋转运动?如图1-4所示,假定除在一条口径均匀的环状闭合管子里的液体外,液体突然处处都被冻结了。也就是说,管外的液体都停止了流动,但由于被禁锢的流体内存在着动量(这就是说,围绕管子沿一个方向的动量大于沿另一个方向的动量),所以管内的液体仍可继续流动。我们把管内液体的有效速率乘以该管周长这个量定义为环流 。我们再把上述概念加以引申,而定义任一矢量场的“环流”(即使没有任何东西在流动亦然)。对于任一矢量场,绕任一想象中的闭合曲线的环流 可以定义为矢量(沿一致向指)的平均切向分量乘以该回路的周长(图1-5),即
环流=(平均切向分量)·(绕行距离). (1.5)
你们将会看到,这一定义确实给出了一个正比于上述迅速被冻结的管子里的环流速度的数值。
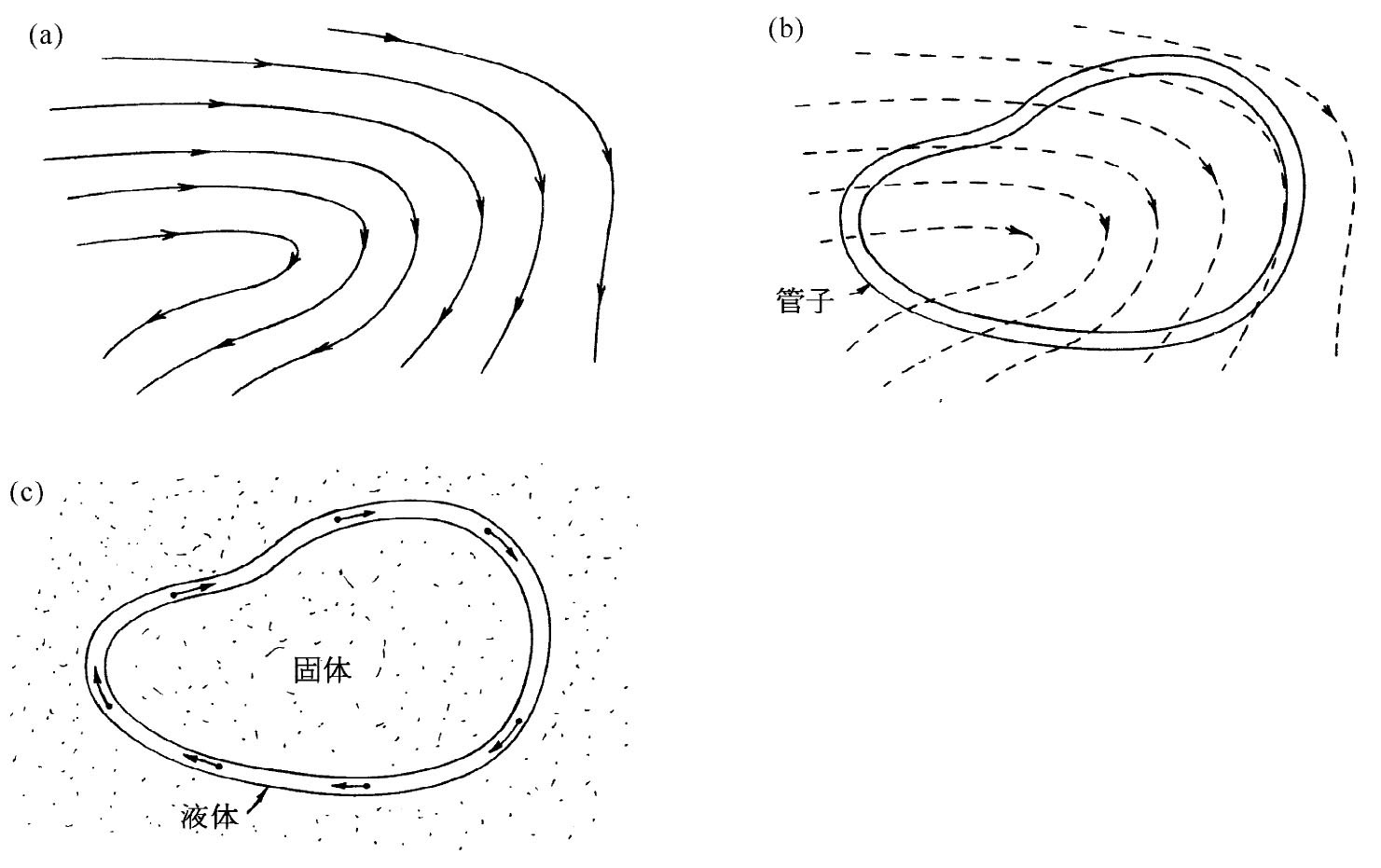
图1-4 (a)液体中的速度场;设想有一截面均匀、按照图(b)所示的任一闭合曲线安放的管子;假如液体除管内的外,处处都被冻结,那么管里的液体便将按图(c)所示的那样循环流动
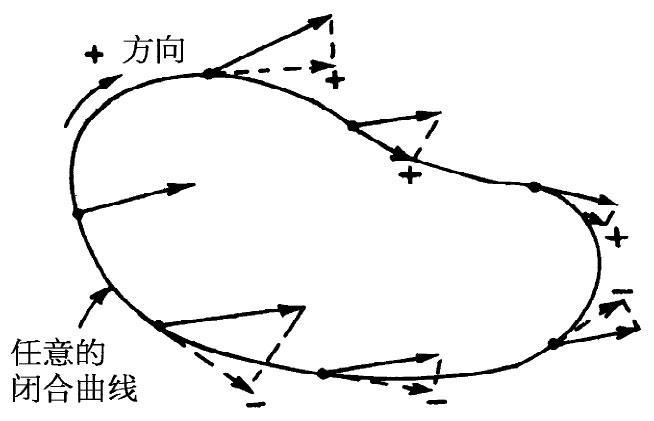
图1-5 矢量场的环流等于矢量(沿一致向指)的切向分量平均值乘以该回路的周长
只要利用这两个概念——通量与环流——我们就能立即描述电学和磁学的所有定律。你可能不会一下子就理解其意义,但它们将给出有关电磁方面物理学基本描述方法的一些概念。