
电磁学第一个定律对电场通量是这样描述的:

式中∈0 是一常数。如果在闭合曲面内没有电荷,即使在曲面外附近存在电荷,E的法向分量的平均值 仍然等于零,所以并没有净通量通过该曲面。为了证明这种表述是强有力的,只要再加上来自单个电荷的场是球对称的这个概念做准备,就可以证明式(1.6)与库仑定律是等同的。对于一个点电荷,我们做一个包围该电荷的球面,那么,平均法向分量就正好等于E在任一点的量值,因为这个场必定是径向的,并且在球面上的任一点具有相同的强度。现在法则讲,在球面上的电场乘以球面面积——即跑出去的通量——正比于球面内的电荷。要是使球的半径增大,则面积按半径的平方增加;电场的平均法向分量乘以该面积仍需等于球面内的电荷,因而该场必定随距离的平方减弱。这就得到了一个“负二次方的”场。
在空间如果我们有一条任意而不动的曲线,并测量电场绕该曲线的环流,那么将发现它一般不等于零(虽则对于库仑定律它为零)。更确切地说,对于电学还存在第二条定律,即对于任一以曲线C为边缘的(非闭合)曲面S,
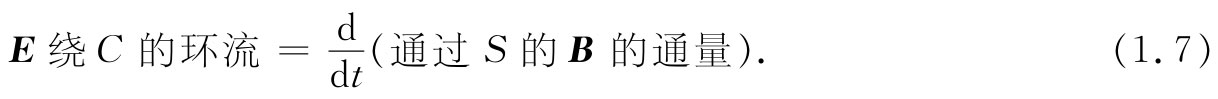
再写出下面两个有关磁场B的相应方程,我们就能完成电磁场的全部规律。
B通过任何闭合曲面的通量=0. (1.8)
对于以曲线C为边界的曲面S,

式(1.9)中出现的常数c2 为光速的平方,它之所以出现是由于磁实际上是电的一种相对论效应。至于插入常数∈0 ,则是为了方便地导出电流的单位。
式(1.6)~(1.9)以及式(1.1)都是电动力学的定律 [2] 。牛顿定律写起来虽然简单,但它会引出一大堆复杂的结果,而你要深入地学习就得花费很长时间。现在这些定律既然写起来就没有那么简单,那当然意味着其结果将更为复杂,所以我们将花大量时间才能把它们全部弄清楚。
通过做一系列小实验(这些实验在定性上表明电场和磁场的关系),我们就能验证某些电动力学定律。当你梳头时,将会对式(1.1)中的第一项有所体验,因而我们就不去证明这一项了。如图1-6所示,给悬挂在一条形磁铁上面的导线输入电流,式(1.1)中的第二项可得以演示。当电流接通时,导线由于受力F=qv×B作用而发生了运动;当存在电流时,线里的电荷在运动,所以它们有一速度v,磁铁产生的磁场就会对它们施加作用力,结果把导线推向一旁。
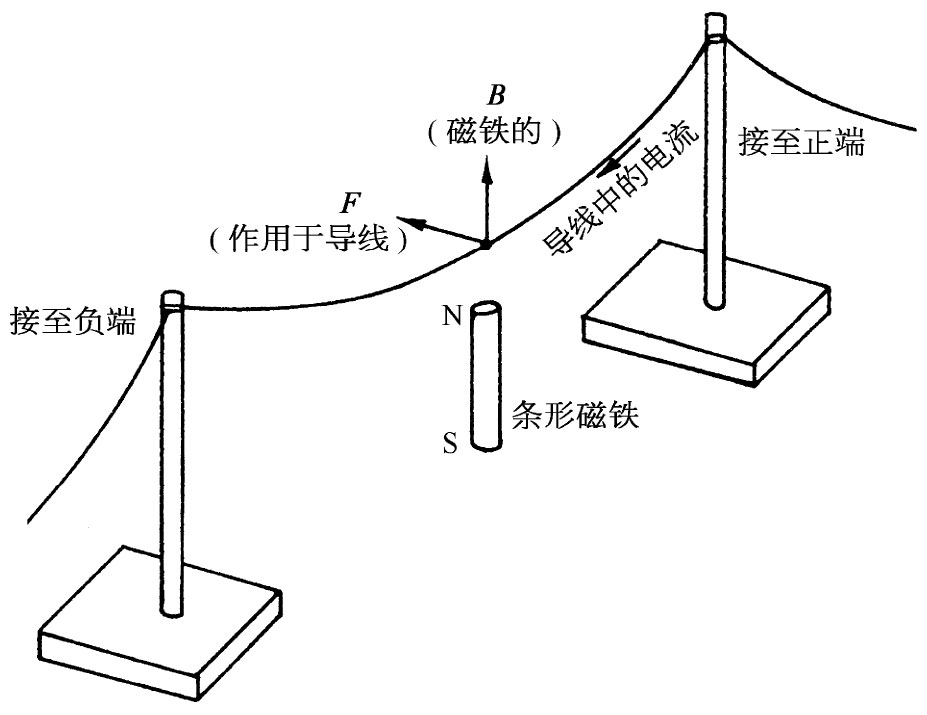
图1-6 一条形磁铁在导线处给出了磁场B。当有电流沿导线流动时,该导线由于受力F=qv×B的作用而运动
当导线被推向左边时,我们会预料到磁铁必定感受到被推向右边。否则就可将整套设备装在一辆车子上而构成一个动量不守恒的推进系统!虽然这力太小、不足以使磁铁的运动看得见,但被更加灵敏地支撑着的一根磁铁,比如像指南针那样,就会显现出运动来。
导线为什么会推磁铁呢?导线里的电流会产生它自身的磁场,从而施力于磁铁上。按照式(1.9)中的第二项,电流必有一个B的环流 ——在这种情况下,B线就是环绕该导线的回路,如图1-7所示。作用于磁铁上的力,就是由这B产生的。
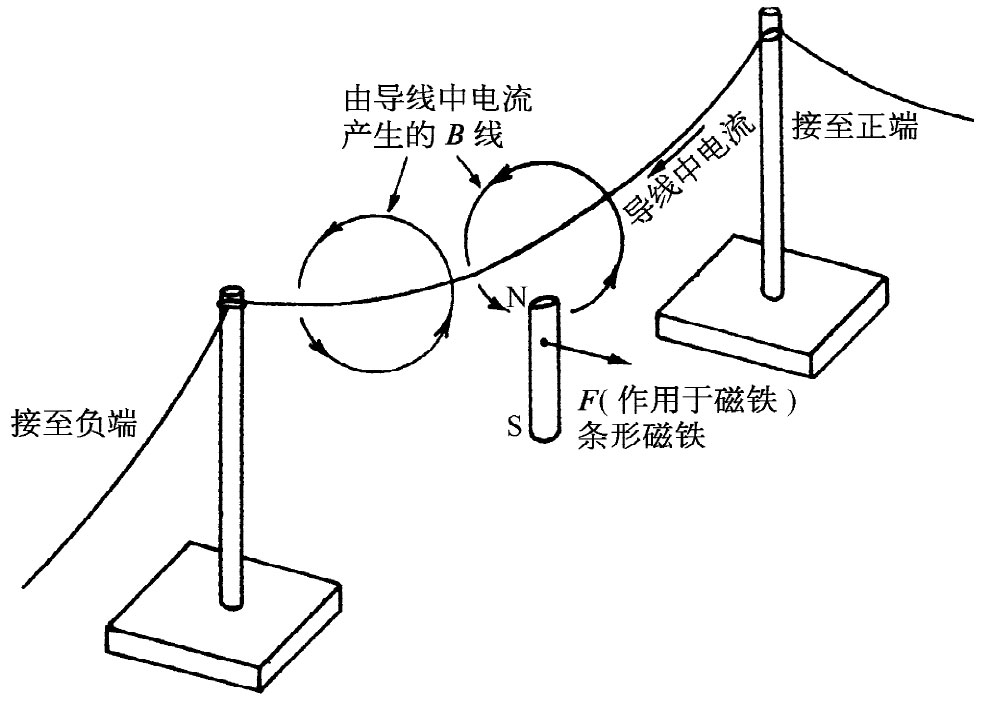
图1-7 导线的磁场施力于磁铁
式(1.9)还告诉我们,对于通过导线的一个恒定电流,对围绕导线的任何 曲线B的环流都相同。由于曲线——比方说是一圆周——距离导线越远,则其周长越长,B的切向分量就必然减小。你可以看到,事实上我们该期待B随着离开长直导线的距离线性地减弱。
现在,我们已经说过,流经导线的电流会产生磁场;而当有磁场存在时,就有一力作用于载有电流的导线上。于是我们也预料到,如果用导线中的电流来产生磁场,则它会对另一载流导线施一作用力。这可由采用如图1-8所示的两根悬挂导线来做演示。当两电流同向时,两导线相吸;但当两电流方向相反时,它们将相斥。
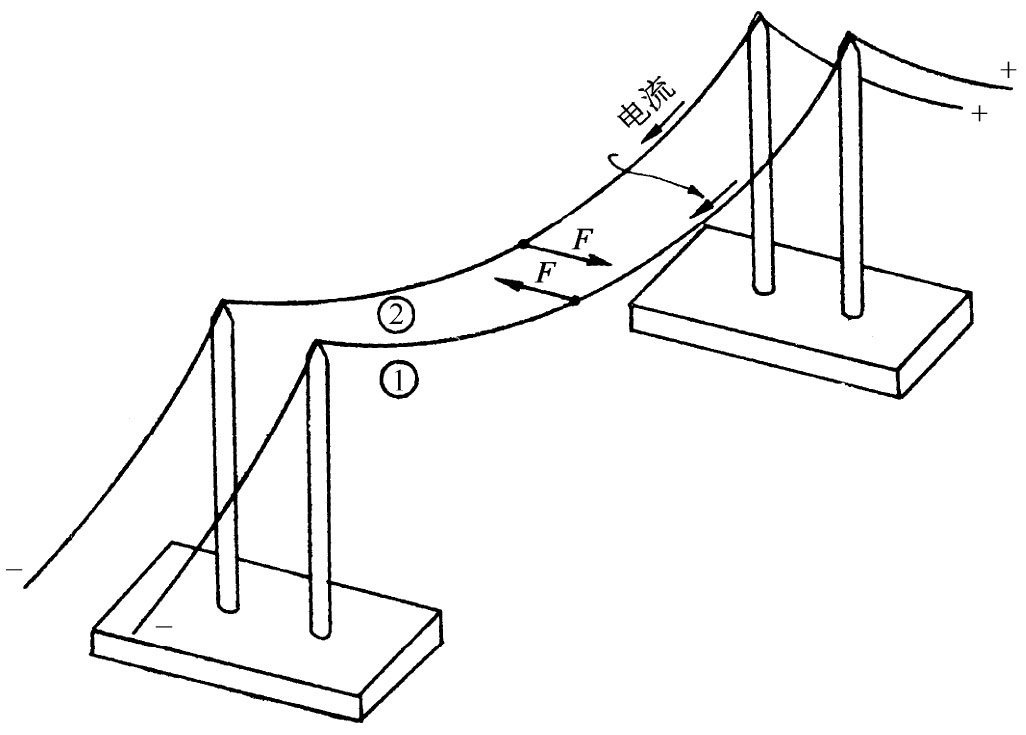
图1-8 两条通电流的导线互相有力作用着
简言之,电流和磁铁均会产生磁场。且慢!试问磁铁究竟是什么?如果磁场是由运动电荷产生的,那么,来自一块磁铁的磁场是否有可能也是由于电流的原因呢?看来的确是这样。我们可以将实验中的条形磁铁用一个导电线圈来代替,如图1-9所示。当电流通过线圈——同时也有电流通过在线圈上面的那根直导线——时,我们便会观察到导线的运动与以前用磁铁而不用线圈时完全一样。换言之,线圈里的电流模仿了一块磁铁。因此,看来一块磁铁的作用就如同它含有一种永恒的环行电流一样。事实上,我们可以用铁原子中的恒定电流来理解磁铁。在图1-7中,作用在磁铁上的力就是由式(1.1)中的第二项引起的。
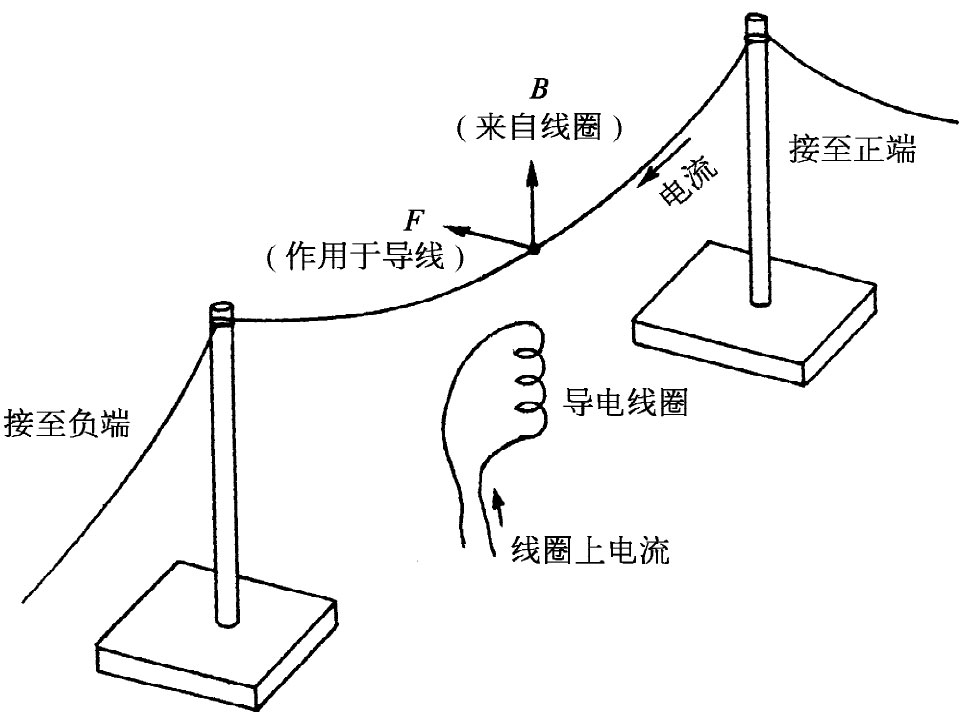
图1-9 图1-6中的磁铁可用一个载流线圈来代替,有一相似的力作用在导线上
究竟这些电流是从哪里来的呢?一种可能来自原子轨道中电子的运动。实际上虽然对于某些材料来说这是正确的,但对铁来说却是不正确的。一个电子,除了在原子中环行之外,还绕它本身的轴旋转——有些像地球的自转——正是由于自旋所产生的电流才为铁提供了磁场(我们说“有些像地球的自转”,是因为这一问题在量子力学中竟是那么奥妙,以致一些经典概念并不能真正恰当地描述这些事物)。在大多数物质中,有些电子这样自旋,另一些电子那样自旋,所以磁性互相抵消;可是在铁里——由于某个我们将在以后加以讨论的神秘原因——有许多电子却绕着它们的排列整齐的轴旋转着,这正是磁性的起源。
由于磁铁的场都是来自电流,所以我们无需因存在磁铁而在式(1.8)和(1.9)中引进任何额外的项。我们只要取所有 的电流,包括自旋电子的环行电流,那么该定律就对了。但你亦应注意,式(1.8)说明不存在与出现在式(1.6)右边的电荷相类似的磁“荷”。没有人曾发现过磁荷。
式(1.9)右边的第一项是由麦克斯韦从理论上发现的,而且十分重要。它说明一个变化着的电场会产生磁场。事实上,若没有这一项,该方程便毫无意义。若无此项,则在一非完整的回路中便不会有电流。但正如我们在下述例子中将见到的这样的电流确实存在。设想一个由两块平行板构成的电容器,它正在充电,电流流向其中一极板而流出另一极板,如图1-10所示。若围绕着其中一条导线画一条曲线C,并用一个被该导线贯穿的、如图中所示的S1 面来盖满这条曲线,按照式(1.9),B绕C的环流由导线中的电流乘以c2 给出。可是若我们用另一个形状像碗、并通过电容器两板间、始终保持在导线外面的一个不同 的曲面S2 来盖满,那又将怎样呢?肯定不会有任何电流通过这一个曲面。然而,仅仅改变一下想象中的曲面位置,总绝不会改变一个实际的磁场吧!B的环流必然和以前一样。是的,对于S1 和S2 两个面,式(1.9)右边的第一项和第二项相结合,确实会给出相同的结果。对于S2 来说,B的环流由电容器两板间E的通量的变化率给出。可以通过计算证明,正在变化着的E与电流之间是用那种使式(1.9)保持正确所必需的方式相联系的。麦克斯韦看到了它的必要性,因而首先写出了完整方程。
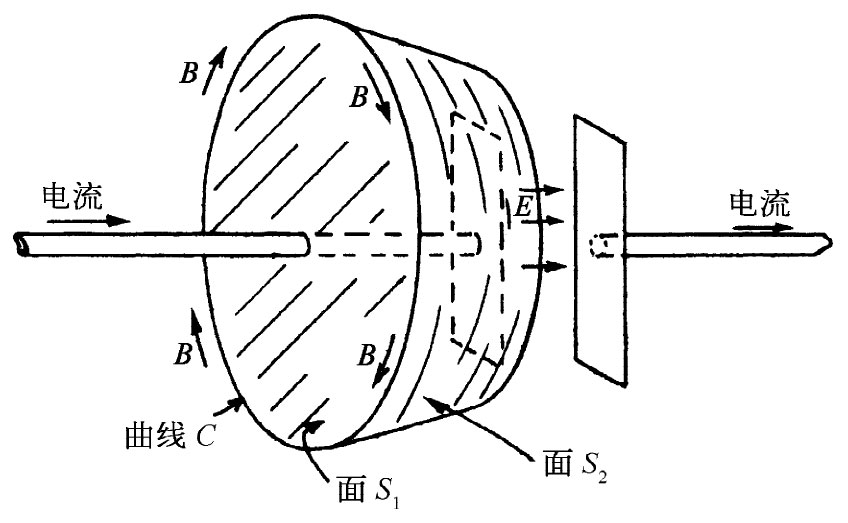
图1-10 B绕曲线C的环流,既可以由通过面S1 的电流给出,也可以由通过面S2 的E的通量变化率给出
采用图1-6所示的那种装置,我们可以演示另一个电磁学定律。将悬挂导线两端从电池上断开,接在一个电流计上,它会告诉我们何时有电流通过该导线。当在磁铁产生的磁场中向旁推动 导线时,便会观察到电流。这样一个效应恰恰是式(1.1)的另一个结果——导线中的电子感受到了力F=qv×B。电子之所以具有侧向速度,是因为它们随导线一起运动。这个v同来自磁铁的垂直方向的B一起产生了一个作用于电子上的、沿 导线方向的力,此力引起电子向电流计运动。
然而,假定我们移动的不是导线而是磁铁,从相对性来讲,可猜测到这不应当产生任何差别。的确,我们在电流计中观察到一个相似电流。磁场怎么会产生作用于静止电荷上的力呢?按照式(1.1)一定存在一个电场。一根运动的磁铁必定产生电场。这过程怎样发生,可以由式(1.7)定量地给予说明。这个方程描述了许多具有巨大实际价值的现象,诸如那些出现在发电机和变压器中的现象。
我们的方程组最引人注目的一个结果是,式(1.7)和(1.9)包含着关于在很大距离范围内的电磁辐射效应的解释。解释大致如下:假设由于导线里电流突然接通,就使得某处的磁场增大;于是,根据式(1.7)就必然存在一个电场的环流;当这建立起来的电场产生环流时,根据式(1.9)又一个磁的环流将形成;可是,这个 磁场的建立又将产生一个新的电场环流……依此类推。就这样,场在通过空间前进时,除了在它们的发源处外,并不需要电荷或电流。这就是我们都能够互相看见 的关键所在!这一切都存在于电磁场的方程组中。