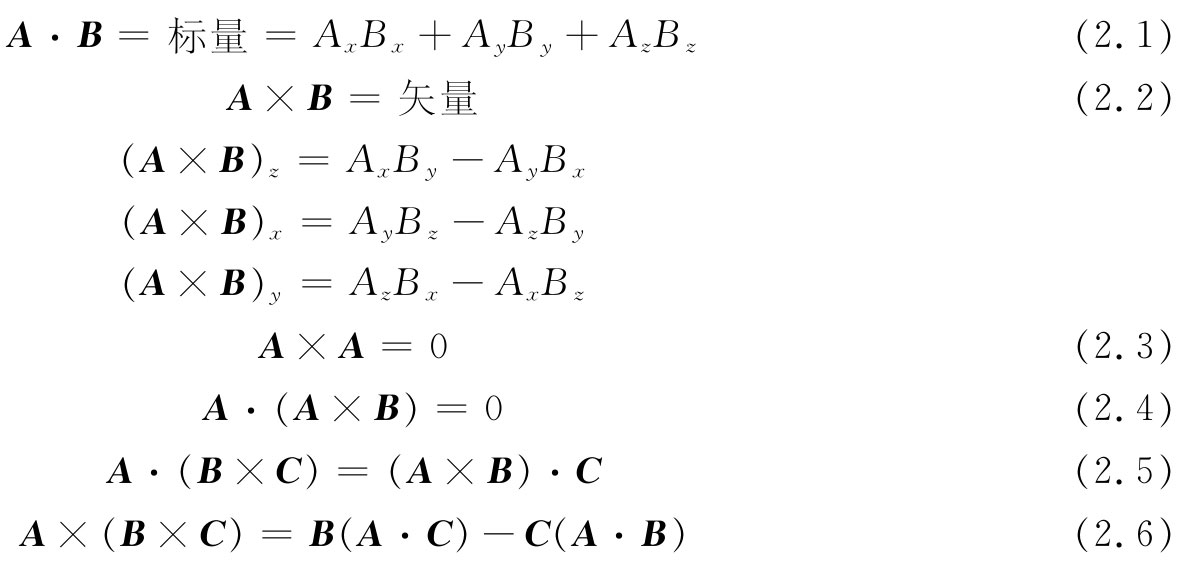
现在我们从电磁理论抽象的、数学的观点开始。目的是解释第1章中所给出的那些定律的意义。而为了做到这一点,必须首先对一种将要用到的、新的特殊符号加以解释。所以就让我们暂时忘却电磁学而讨论矢量场的数学。这不但对于电磁学而且对于所有物理情况都是十分重要的。正如通常微积分学对于所有物理部门都那么重要一样,矢量的微分学也是如此。我们就转到这么一个科目上来吧。
下面列举一些来自矢量代数的等式,并假定你们都已知道了。
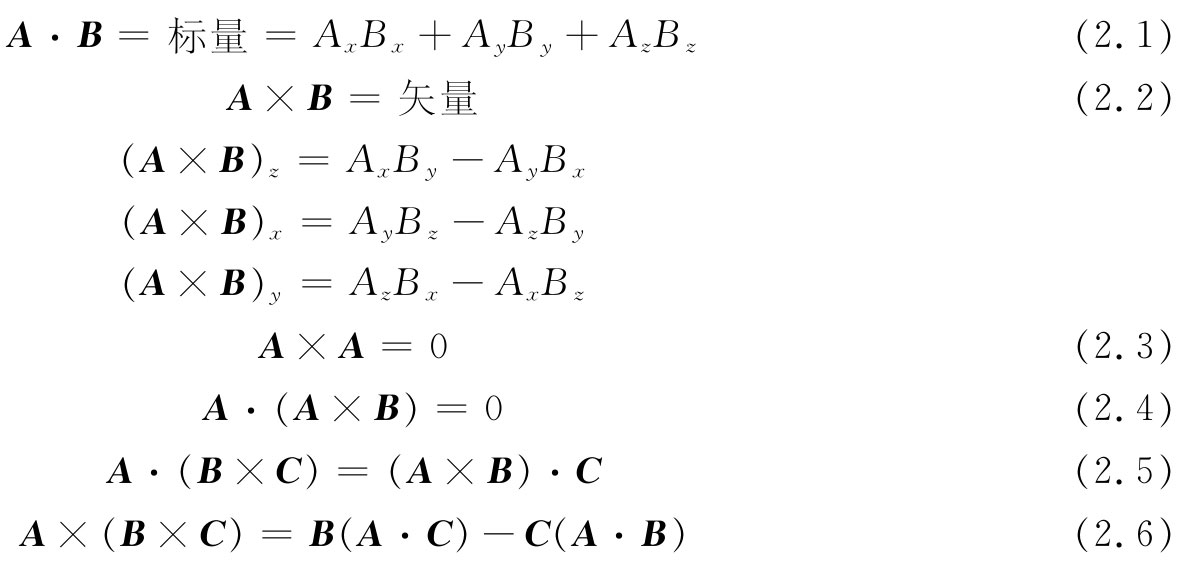
我们也要用到从微分学方面得来的下列两个等式:
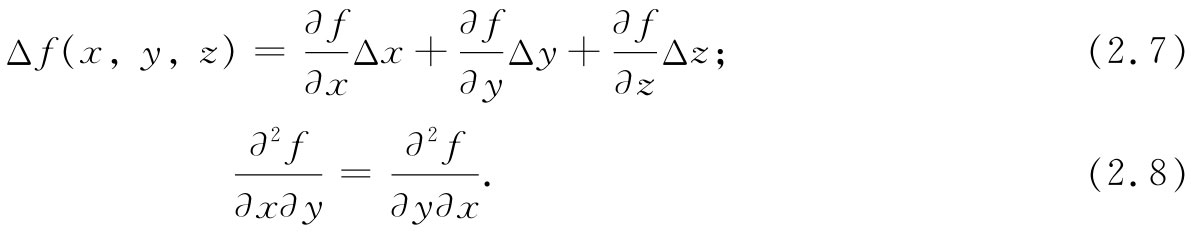
当然,第一个等式(2.7)只有在Δx,Δy,Δz都趋于零的极限时才正确。
可能存在的最简单的物理场是标量场。你应当记得,我们所说的场是指取决于空间位置的一个量。所谓标量场 ,仅指每点由单一的数值——一个标量——标志的场。当然这个数值可随时间而变,但眼前我们还无需为此操心。我们将只谈论在某一给定时刻场看来是个什么样子。作为标量场的一个例子,试考虑一块固体材料,其中某些地方加热而另一些地方受冷,使得该物体的温度以一种复杂的方式逐点改变。于是温度将是在某直角坐标系中测得的空间位置(x,y,z)的函数,所以温度是一标量场。
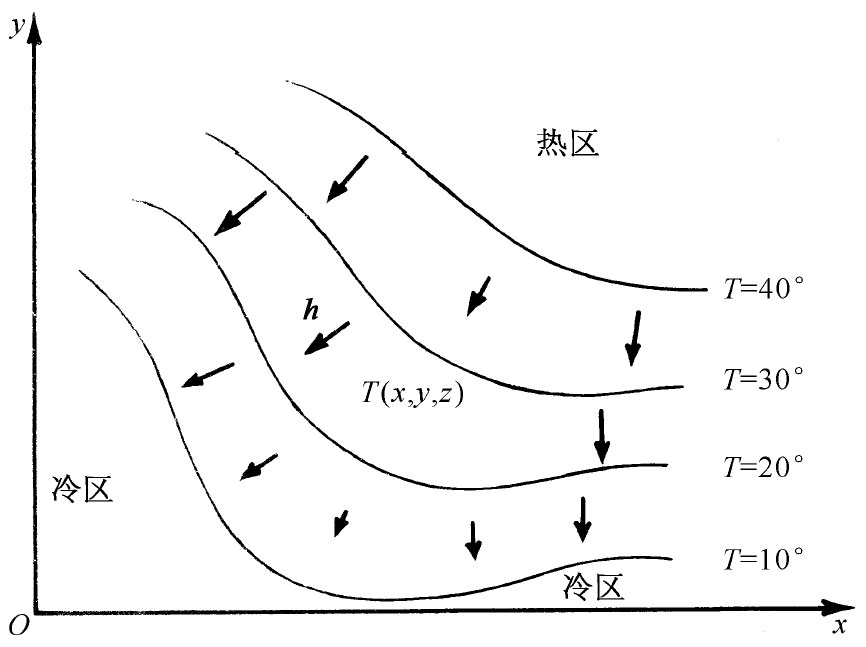
考虑标量场的一种办法是去设想一些“等值面”,即通过所有相同值的场点画成的想象中的面,正如在地图上那些由等高点连成的等高线一样。对于一个温度场来说,这些等值面被称为“等温面”或等温线。图2-1表示一温度场,并表明在z=0处T对x和y的关系。在该图上画出了几条等温线。
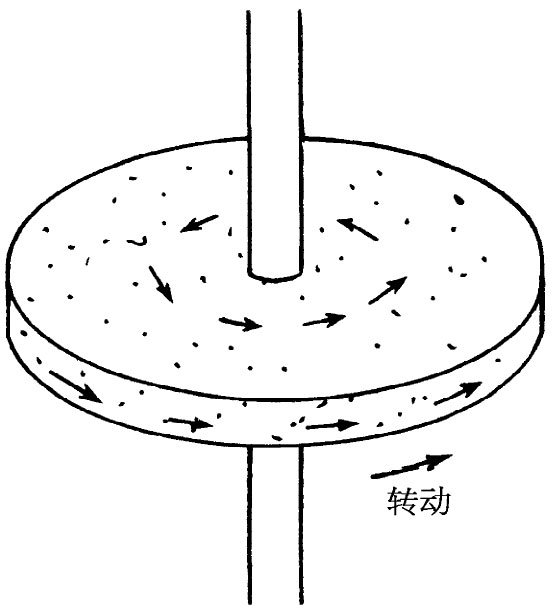
还存在一种矢量场,概念也十分简单,就是在空间的每一点给出一个矢量,这个矢量逐点变化。作为一个例子,可考虑一个旋转物体。在任意点物体中物质的速度便是一个矢量,它是位置的函数(图2-2)。作为第二个例子,考虑在一块材料里的热流。如果在材料中某处的温度较高另一处的温度较低,则热量就会从较热处流至较冷处。在材料中的不同位置热量将朝不同的方向流动。这一热流就是一个有方向的量,我们称其为h。它的大小是有多少热量在流动的量度。关于热流矢量的例子也如图2-1所示。
|
|
| 图2-1 温度T是标量场的一个例子。与空间每一点(x,y,z)相联系的是一个数值T(x,y,z)。处于标记着T=20°的曲面(图中所示为z=0处的一条曲线)上所有的点都有相同温度。箭头是热流矢量h的一些样品 | 图2-2 旋转物体中原子的速度是矢量场的一个例子 |
让我们对h下一个更准确的定义:热流矢量在一点的大小就是在单位时间内通过垂直于流动方向的无限小面积元上单位面积的热能。这个矢量指向热量流动的方向(见图2-3)。用符号表示为:若ΔJ为单位时间内通过面积元Δa的热能,则
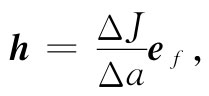 (2.9)
(2.9)
式中ef 是沿流动方向的单位矢量 。
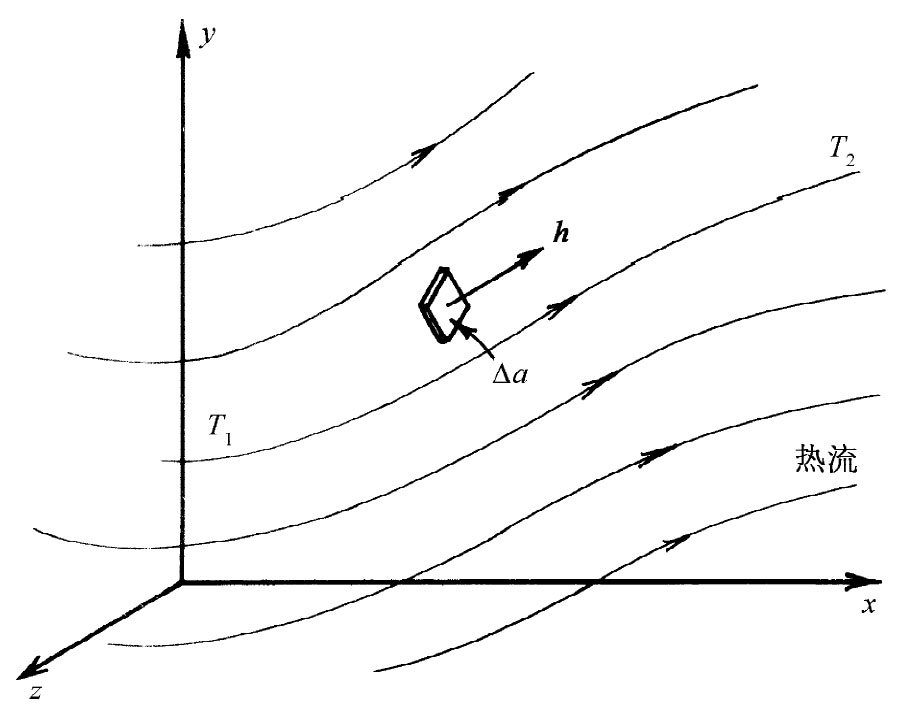
图2-3 热流是一种矢量场。矢量h指向热量流动的方向。它的大小则是单位时间内流过垂直于流动方向的面积元的能量除以该面元的面积
矢量h也可按另一种方式——用它的分量——来下定义。我们试问,有多少热量会通过一个与流动方向成任意 角度的小面积。在图2-4中,我们表示一个小面积元Δa2 与垂直于热流的另一个小面积元Δa1 相倾斜。单位矢量 n与面积元Δa2 垂直。n与h之间的夹角就等于两个面积元之间的角度(因为h垂直于Δa1 )。那么,每单位时间内 通过Δa2 的热量有多少呢?通过Δa2 的热量就等于通过Δa1 的,只不过面积不同罢了。事实上,Δa1 =Δa2 cosθ。因此,通过Δa2 的热流为

我们对此式加以说明:通过单位法线为n的任何 面积元的热流(单位时间、单位面积)为h·n。同样可以说:垂直于面积元Δa2 的热流分量为h·n。如果愿意,也可以认为这些说法定义 了h。我们也将把这些相同概念应用于其他矢量场。
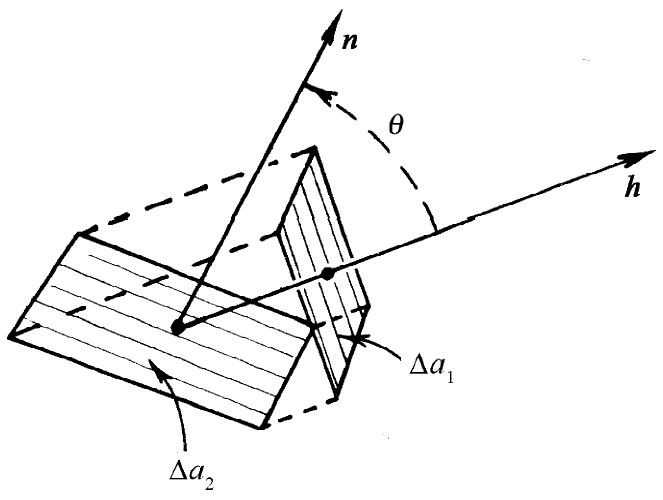
图2-4 流经Δa2 的热量与流经Δa1 的相同