
迄今我们只有一阶微商。为什么就没有二阶微商呢?我们可以有下列几种组合:

你可以核实一下,这些全是可能的组合。
让我们首先看一看第二式(b)。与它相同的形式为
A×(AT)=(A×A)T=0,
因为A×A恒为零。因此,我们就有:
curl(grad T)=▽×(▽T)=0. (2.46)
如果用分量来计算一遍,便可以看出这个式是怎样产生的:
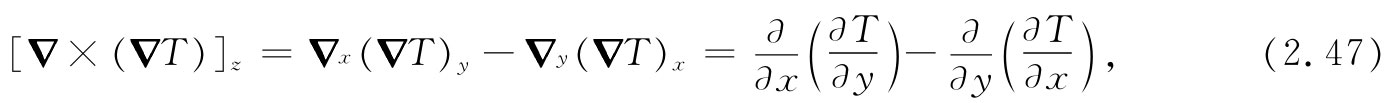
上式等于零[根据式(2.8)]。对于其他分量也是如此。因此,对任何一种温度分布(实际上,对于任何 标量函数),▽×(▽T)=0。
现在让我们举出另一个例子,看看能否找到别的等于零的等式。一个矢量与一个其中含有该矢量的矢积的点积为零,即
A·(A×B)=0, (2.48)
因为A×B垂直于A,所以在A方向上就没有A×B的分量。与此相同的一种组合出现在式(2.45)的(d)中,因而我们有:
▽·(▽×h)=div(curlh)=0. (2.49)
此外,用分量进行运算来证明上式为零并不困难。
现在我们将不加证明地陈述两个数学定理。它们是物理学家已经知道的十分有趣而又有用的定理。
在一个物理问题中,我们经常发现某一个量——比如矢量场A——的旋度为零。如我们已由式(2.46)看到,一个梯度的旋度为零,这是很容易记住的,因为这种情形是矢量造成的。于是,有可能肯定A是某一个量的梯度,这样它的旋度才必然等于零。这个有趣的定理说明,如果curlA等于零,则A总是某种东西 的梯度——存在某一标量场ψ使得A等于gradψ. 换句话说,我们有
定理 :

若A的散度为零,则有一个相似的定理。我们已从式(2.49)看到,某个矢量旋度的散度总是零。如果你遇到divD为零的一个矢量场D,那你就可以得出结论,D是某个矢量场C的旋度。
定理 :

在考察两个算符的可能组合中,我们已经找出其中有两种组合总是等于零。现在来看看那些不 等于零的组合。取出表上所列的第一个组合▽·(▽T)。我们把它写成分量式:
▽T=(▽x T,▽y T,▽z T).
于是
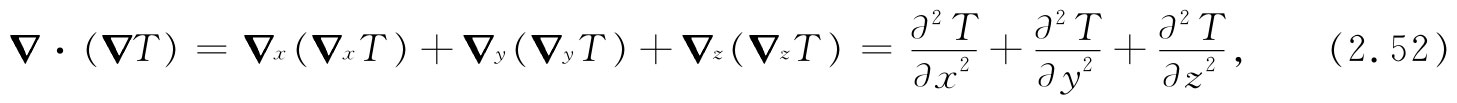
上式一般应给出某个数,它是一个标量场。
你看到,上式无需保留那个括号,因而在不会引起混乱的情况下它可以写成:
▽·(▽T)=▽·▽T=(▽·▽)T=▽2 T. (2.53)
这里我们把▽2 看成一个新的算符。这是一个标量算符。由于它经常出现在物理学中,因而已被赋予一个专用名称,即拉普拉斯算符 。
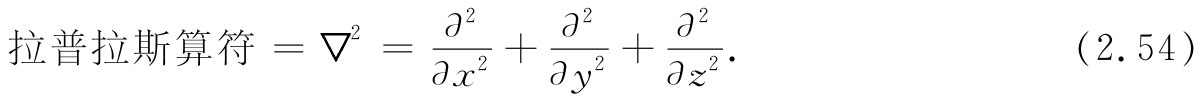
由于拉普拉斯算符是一个标量算符,就可以用它来对一矢量进行运算——这意味着对在直角坐标系的每一个分量进行同一种运算:
▽2 h=(▽2 hx ,▽2 hy ,▽2 hz ).
让我们再来看另一个可能性:▽×(▽×h),那是表(2.45)中的(e)。现在如果我们应用矢量等式(2.6):
A×(B×C)=B(A·C)-C(A·B), (2.55)
便可以把一个旋度的旋度写成不同的形式。为了使用这一公式,我们应当用算符▽来代替其中的A和B,并令C=h。这样就得到:
▽×(▽×h)=▽(▽·h)-h(▽·▽)…???
但请等一等!有点不对了。前两项不错,那都是矢量(算符被满足了),可是末项就不知会产生出什么东西来。它仍然是一个算符。麻烦在于我们曾经不够小心,以致不能保持各项的前后次序。然而,若你再看一看式(2.55),就会见到我们同样可以把它写成:
A×(B×C)=B(A·C)-(A·B)C. (2.56)
这几项的次序看来要好些。现在在式(2.56)中做代换,便得:
▽×(▽×h)=▽(▽·h)-(▽·▽)h. (2.57)
这个形式看来不错。事实上,它是正确的,例如你可以通过计算分量给以证明。末项就是拉普拉斯算符,因而我们同样可以写成:
▽×(▽×h)=▽(▽·h)-▽2 h. (2.58)
除了(c)▽(▽·h)以外,我们对于表中的双▽的组合全都谈过一些了。它可能是一个矢量场,但却没有什么特殊情况可说的。那不过是偶尔会出现的一种矢量场罢了。
把我们的结论列成一表将很方便:

你可能会注意到,我们从未试图发明一个新的矢量算符(▽×▽)。你看这是为什么?