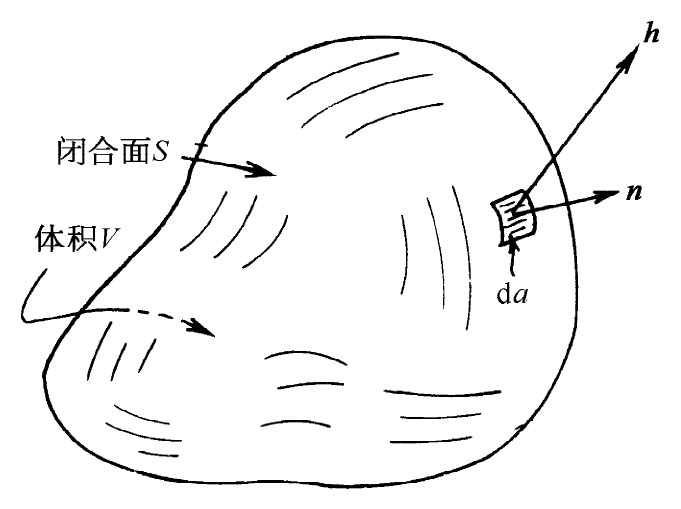
在讨论下一个积分定理——关于散度方面的定理——之前,我们想学习一下物理意义较明显的关于热流的某种概念。我们曾定义过矢量h,它代表单位时间内通过单位面积的热量。假设在一块材料内部,有一个包围着体积V的某闭合曲面S(图3-3)。我们希望求出从这个体积 里流出去的热量有多少。当然,我们可以通过计算流出表面 S的总热量来求得它。

图3-3 闭合面S规定了体积V。单位矢量n是面积元da的外法线,而h则是该面积元处的热流矢量
我们用da记为一个面积元的面积,这符号代表一个二维微分,例如,若该面积碰巧处在xy面上,则应有
da=dxdy.
由于以后还将对体积进行积分,所以,为方便起见,考虑一个小立方体的微分体积。这样,当我们写出dV时,指的就是
dV=dxdydz.
有些人不喜欢写成da,而喜欢写成d2 a以提醒人们注意那是一个二级量。他们同样不想用dV而要用d3 V。我们则将采用那种较简单的符号,并假定你确能记住面积具有二维,而体积具有三维。
通过面积元da流出的热量等于该面积乘以垂直于da的h分量。我们已把n定义为与表面成直角而指向外的单位矢量(图3-3)。希望得到的h分量为:
hn =h·n. (3.9)
于是,通过da流出的热量为
h·nda. (3.10)
为了得到通过任意表面的总热量,我们对来自所有面积元的贡献求和。换句话说,将在整个表面对式(3.10)进行积分:
通过S向外流出的总热量=∫S h·nda. (3.11)
我们将把这个面积分称为“h通过该表面的通量”。通量这个词的原有意义是流量,因而面积分恰好意味着h通过该表面的流量。可以认为:h是热量流动的“流密度”,而它的面积分则是指向表面外的总热量流,也就是单位时间流出的热能(每秒的焦耳数)。
我们希望把这一概念推广到矢量并不代表任何流动的东西那种情况。例如,它或许是电场。如果我们乐意的话,肯定也能对电场的法向分量在一个面上积分。尽管这并不是什么东西的流动,但我们仍称之为“通量”。我们说,
E通过曲面S的通量=∫S E·nda. (3.12)
这就把“通量”这一词推广到指一矢量的“法向分量的面积分”了。即使所考虑的表面不是闭合的情况,我们也将使用同样的定义,就像这里讨论闭合面那样。
回到热流的特殊情况,让我们以热量守恒 的情况为例。例如,设想有某件材料初始加热以后就不再有热量产生或吸收。于是,如有净热量从闭合表面流出去,则该体积内热的含量就一定会减少。所以,在这种情况下热量应该守恒,我们说:

式中Q是表面S内的热量。从S面出来的热通量等于S面内总热量Q对于时间变化率的负值。这种解释是可行的,因为我们正在谈论热流,而且已假定热量是守恒的。当然,假如那时热量正在产生,则我们也许就不能谈论该体积内的总热量了。
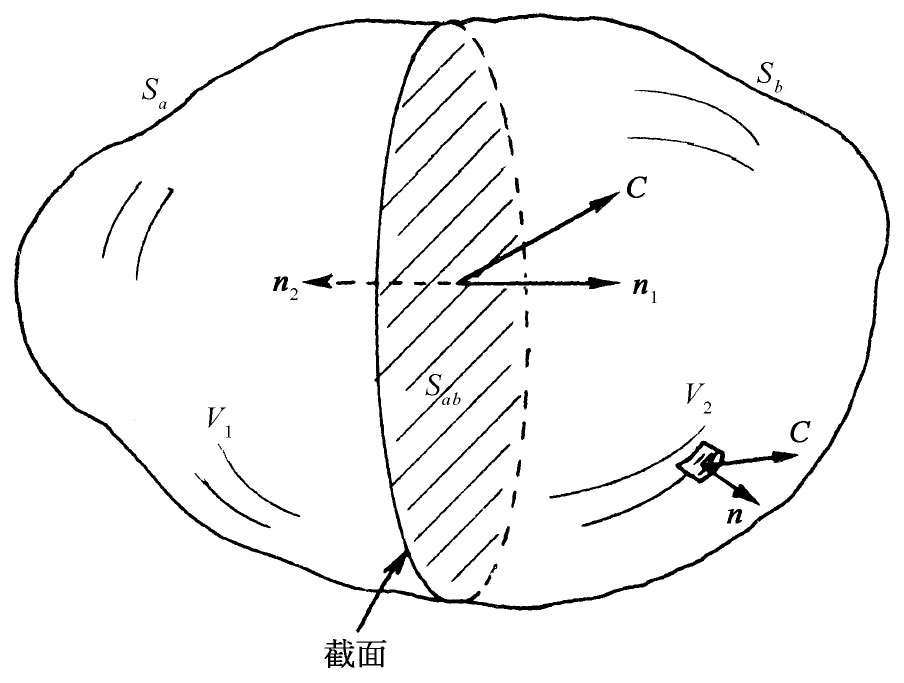
图3-4 包围在S面内的体积V被一“截面”Sab 分成两半。现在就有了包围在S1 =Sa +Sab 面内的体积V1 和包围在S2 =Sb +Sab 面内的体积V2
现在我们要指出一个关于任意矢量的通量的有意义的事实。如果愿意,你可以认为这矢量是热流矢量,但我们所要讲的内容对任一矢量场C都将是正确的。设想有一包围体积V的闭合曲面S,现用如图3-4所示的某种“截面”将体积分成两部分,我们就有两个闭合曲面和体积。体积V1 被曲面S1 包围,由原来表面的一部分Sa 和截面Sab 构成。体积V2 被曲面S2 包围,由原来表面的其余部分Sb 再加上截面Sab 构成。现在考虑下述问题:假设要计算通过曲面S1 的向外通量,再加上通过曲面S2 的向外通量。这个总和是否会等于通过开始时那个完整表面的通量呢?答案是肯定的。通过S1 和S2 所共有的Sab 面部分的通量恰好互相抵消。关于从V1 出来的矢量C的通量,我们可以写成:
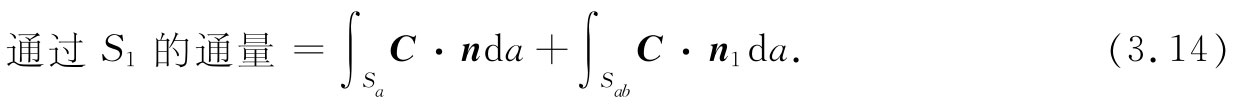
而从V2 流出的通量,则是:

注意!在这两个积分中,n1 表示Sab 属于S1 时的外法线,而n2 则表示Sab 属于S2 时的外法线,分别如图3-4所示。显然,n1 =-n2 ,因而
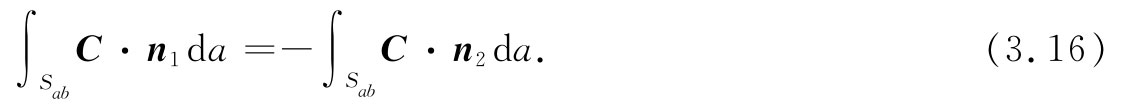
现在若把式(3.14)和(3.15)相加,则通过S1 和S2 两通量之和恰好等于那两个积分之和,而把这两个积分合在一起,就给出通过原来的曲面S=Sa +Sb 的通量。
我们看到,通过整个外表面S的通量,总可以认为是该体积分成两部分后所得到的通量之和。还可以照样再分割下去——例如把V1 再分成两块,你会看到同样的论证仍然适用。因此,不管将原来体积按何种 方式分割,普遍正确的结果应该是:由原来积分表示的、通过外表面的通量,等于出自内部所有各小块的通量之和。