仅仅为了熟悉高斯定理，让我们考虑应用该定理的一个例子。仍然举金属中的热流为例，假定其中所有热量都已预先输入、而此刻正在冷却的那种简单情况。这里没有热源，所以热量是守恒的。那么，在任意时刻存在于某个特定体积里的热量到底有多少呢？它所减少 的量必须恰好等于从该体积表面流出的量。如果我们的体积是一个小立方体，则根据式（3.17）就应该写成：
流出的热量=∫表面 h·nda=▽·hΔV. （3.19）
这必然要等于小立方体内部热量的损失率。设q为单位体积内的热量，则在该立方体内的热量为qΔV，其损失 率则为：
比较式（3.19）和（3.20），我们见到：
仔细注意这个方程的形式，它是物理学中经常出现的形式，即表达了一个守恒定律——这里是热量守恒。我们曾经在式（3.13）中以另一种方式表示过相同的物理事实。这里是守恒方程的微分 形式，而式（3.13）则是一种积分 形式。
我们通过把式（3.13）应用于一无限小立方体而获得了式（3.21）。我们也可用别的方法去做。对于一个以S面为边界的大体积V，高斯定理表达为：
∫S h·nda=∫V ▽·hdV. （3.22）
应用式（3.21），得出右边的积分恰是-dQ/dt，因而我们又一次得到了式（3.13）。
现在让我们考虑一个不同的情况。想象在一大块材料中有一个很小的洞，里面正在进行某种产生热量的化学反应。我们也可以这样设想，用导线连接一个小小的电阻器，然后通电使之发热。我们将假设热量实际上是在一点上产生的，并令W代表在该点每秒释放出来的能量。我们还假定在体积的其余部分热量始终守恒，而且该热量的产生也已持续了足够长的时间——使得现在任何一处的温度都不再发生变化了。问题是：金属里各处的热流矢量h是什么样子？在每一点有多少热量流过？
我们知道，如果在包围着该热源的闭合曲面上对h的法向分量进行积分，则总会得到W。所有在该点源处陆续产生的所有热量都必定通过该表面流出，因为我们已假定其流动是稳定的。这里有一个困难问题，即要找出一个矢量场，在包围源的任意曲面上积分时该矢量场总给出W。然而，我们可以取一个稍微有点特殊的曲面而使场相当容易地求出。比如取一个半径为R而其中心在源处的球面，并设想热流是沿着径向的（图3-6）。直觉告诉我们，如果该块材料足够大，而我们又不令所取的球面太接近边缘，则h应该是径向的，而且，在球面上所有点其值的大小均应相同。你看，我们正在加入一些猜测工作——常称为“物理直觉”——于数学方面来说，是为了获得答案。
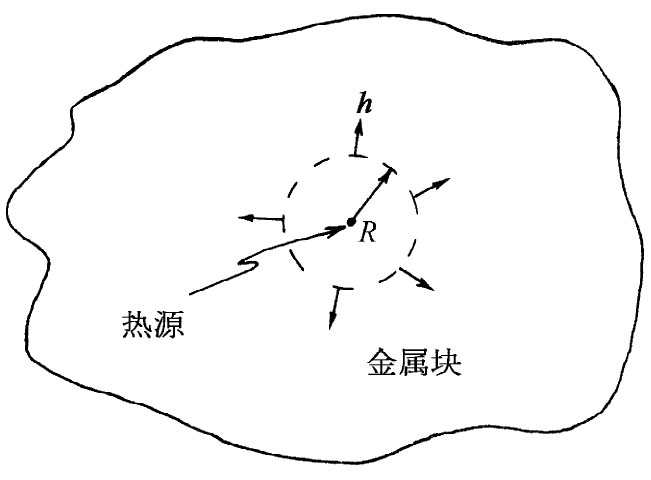
图3-6 在临近一个点热源的区域中，热流沿径向朝外
当h沿着径向而又具有球对称性时，h的法向分量对整个球面的积分将会十分简单，因为法向分量恰好就是h的大小而且是不变的。因积分时所取的面积为4πR2 ，于是就有
∫S h·nda=h·4πR2 （3.23）
（式中h是h的大小）。这积分应等于W，即为源处热量的产生率。因而得：
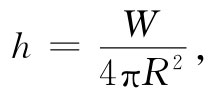
或
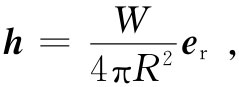（3.24）
式中er 照例代表沿径向的单位矢量。我们的结果说明，h与W成正比而与离源的距离的平方成反比。
刚才所得到的结果，仅适用于点热源附近的热流。现在让我们尝试寻求那种仅在热量守恒的条件下，对最普遍的热流类型也能适用的方程式。这样，我们将只与在任何热源或热吸收体之外的那些地方所发生的情况打交道。
关于热传导的微分方程，曾在第2章中推导过了。根据式（2.44）
h=-κ▽T. （3.25）
应记住这一关系式是近似的，不过对于某些像金属之类的材料该近似相当好。当然，它只在材料里那些没有热量产生或吸收的区域内才适用。我们已在上面导出了另一个关系，即式（3.21），它在热量守恒情况下成立。如果把该方程与式（3.25）相结合，则可得：
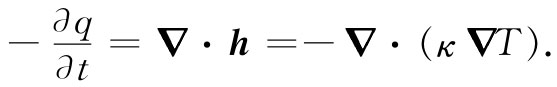
若κ是一常数，则
你会记得，q是单位体积内的热量，而▽·▽=▽2 是拉普拉斯算符
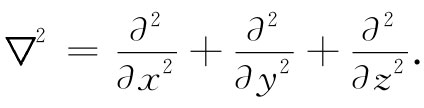
如果我们另外做一个假定，便可得到一个十分有趣的方程式。假定材料中的温度与单位体积的热容成正比——即该材料有确定的比热。当这一假定有效时（往往如此），就可以写成：
Δq=cv ΔT，
或
热量的变化率正比于温度的变化率。这里的比例常数cv 就是单位体积 材料的比热。应用式（3.27）和（3.26），得：
我们已求得，每一点上T的时间 变化率与T的拉普拉斯算符成正比，即与T的空间关系的二阶微商成正比。这样，我们就有一个以x，y，z和t为变量的关于温度T的微分方程。
微分方程式（3.28）称为热扩散方程 。它经常被写成：
式中D叫扩散 常数，在这里等于κ/cv 。
这个扩散方程在许多物理问题中都会出现——气体扩散、中子扩散以及其他各种扩散，我们曾在第1卷第43章中讨论过这类现象的物理性质。现在你们有了一个在最普遍合理的情况下描述扩散的完整方程。往后某个时候我们还将学习一些求解该微分方程的方法，以便找出在特定条件下温度是怎样变化的。现在我们回来考虑有关矢量场的其他一些定理。