现在,我们想用某些考虑散度的同样方法来看待旋度。通过考虑在一个曲面上的积分,我们得到了高斯定理,尽管当初我们打算处理散度时这事还不太明显。我们当时怎么会知道为了得到散度必须在曲面上进行积分呢?根本不清楚会是这个结果。而现在由于显然同样缺乏正当的理由,所以我们还将对矢量做某些计算并证明它与旋度有关。这次计算的将是所谓矢量场的环流。如果C是任意矢量场,取其沿一曲线的分量,并对这一分量自始至终绕整个回路进行积分。这一积分被称为该矢量场绕该回路的环流 。在本章的开头,我们曾经讨论过▽ψ的线积分,现在我们将对任一 种矢量场C求线积分。

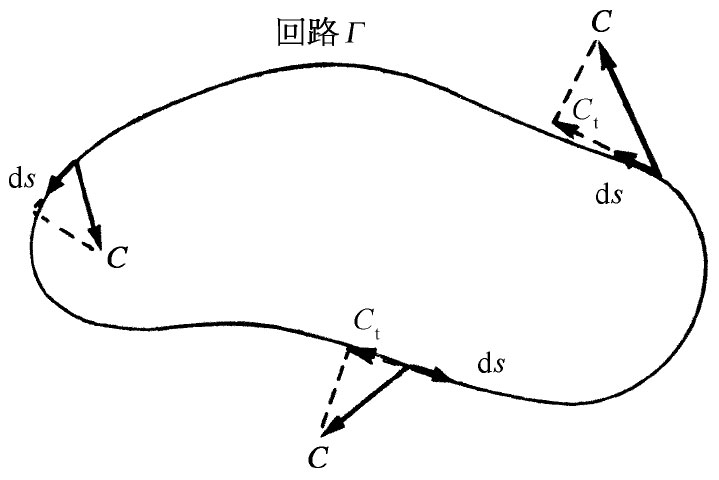
图3-7 C绕曲线Γ的环流为Ct (即C的切向分量)的线积分
设Γ为空间中的任意闭合回路——当然是在想象中的。有一个例子如图3-7所示。C的切向分量绕该回路的线积分可写成:
∮Γ Ct ds=∮Γ C·ds. (3.30)
你应该注意,这积分是始终绕回路取的,并不像以前那样从一点至另一点。在积分符号上的那个小圈圈便是为了提醒人们,该积分是始终绕回路进行的。这一积分叫作该矢量场绕曲线Γ的环流。这个名称原本是从考虑液体的环流来的。但这一名字——正如通量一样——已被推广应用于即使没有物质做“环流”的任何场了。
用对待通量同样的手法,我们可以证明,绕一个回路的环流等于绕两个分回路的环流之和。假设我们在原来曲线上的(1)和(2)两点间用如图3-8所示的割线来连结,就可以将图3-7所示的曲线分成两个回路。现在存在两个回路Γ1 和Γ2 。Γ1 是由处在(1)和(2)左边部分的原有曲线Γa 再加上“捷径”Γab 而构成的。Γ2 则是由原有曲线的其余部分加上该捷径而构成的。
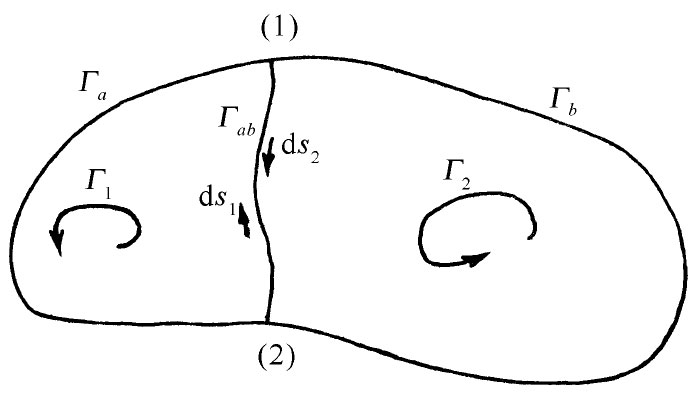
图3-8 绕整个回路的环流等于绕两个回路(Γ1 =Γa +Γab 和Γ2 =Γb +Γab )的环流之和
绕Γ1 的环流等于沿Γa 和沿Γab 两个积分之和。同理,绕Γ2 的环流也是两部分之和,其一沿Γb 而另一沿Γab 。对于曲线Γ2 来说,沿Γab 的积分具有与对曲线Γ1 中沿Γab 的积分相反的符号,因为它们的绕行方向相反——必须按相同的旋转“指向”来进行这两项线积分。
按照我们以前使用过的同样类型的论据,你们可以看到,这两个环流之和将恰好给出绕原来曲线Γ的线积分。那来自Γab 的部分互相抵消了。绕其中一部分的环流再加上绕第二部分的环流等于绕整条外环线的环流。我们可以重复这一过程,把原有回路分割成任意数目的小回路。当将这些小回路的环流相加时,在它们的相邻部分总会互相抵消,从而使其总和相当于绕原来单个回路的环流。
现在让我们假设该原有回路就是某一个曲面的边界。当然,会有无限多个曲面全都以该原有回路为边界。然而,我们的结果将与所选取的曲面无关。首先,将原有回路分割成若干条全都落在所选取的曲面上的小回线,如图3-9所示。不管该曲面形状如何,如果我们选取的小回路足够小,则可以假定每一小回路包围的面基本上是平面。并且,我们也能选取那些小回路使得每个都非常接近正方形。现在就可以通过求绕所有小回路的环流,再取其和,从而算出绕回路Γ的环流。
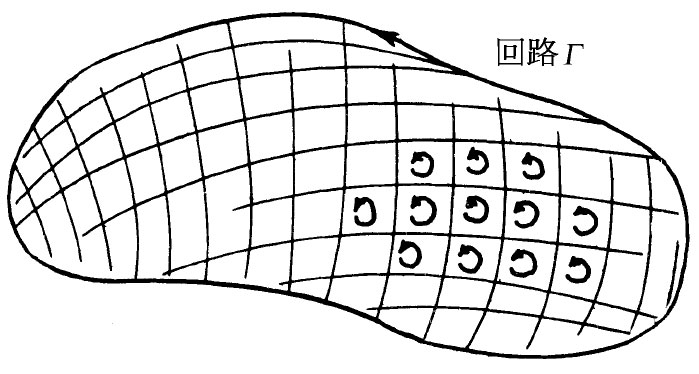
图3-9 选取某一被回路Γ包围着的表面。这个面被分割成若干个小面积,每个近似于一正方形。绕行Γ的环流就等于绕行各小回路的环流之和