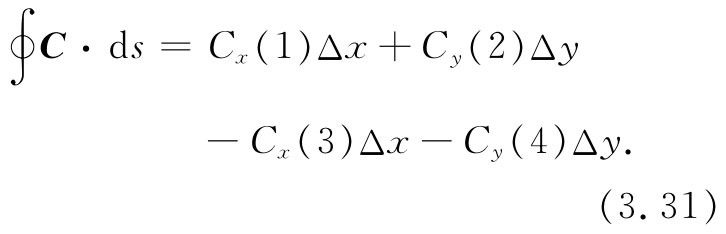
我们将怎样求得沿每一小正方形的环流呢?首先就要问,这一正方形在空间中的取向如何?要是它有一个特殊取向,那计算起来就会方便得多。例如,假使它位于一个坐标平面内。由于对坐标轴的取向我们还未做过任何假设,因此就可以这样选取坐标轴,使此刻我们正专注的那个小正方形正好落在xy面内,如图3-10所示。若该结果用矢量符号来表示,那就可以说,不管该面的特殊取向如何,结果都是一样的。
现在我们希望求出场C绕该小正方形的环流。如果令该正方形足够小,使得矢量C沿它的任一边都不会改变很多,进行线积分就较容易(正方形越小,这个假定就越好,而实际所谈的正是无限小的正方形)。从位于图的左下角那一点(x,y)出发,按照箭头所指的方向绕行一周。沿标记为(1)的第一条边,其切向分量为Cx (1)而长度为Δx。该积分的第一部分就是Cx (1)Δx。沿第二条边,我们获得Cy (2)Δy。沿第三条边得-Cx (3)Δx,而沿第四条边得-Cy (4)Δy。这些负号是需要的,因为这里要求的是沿绕行方向的切向分量。因此,整个线积分就是:
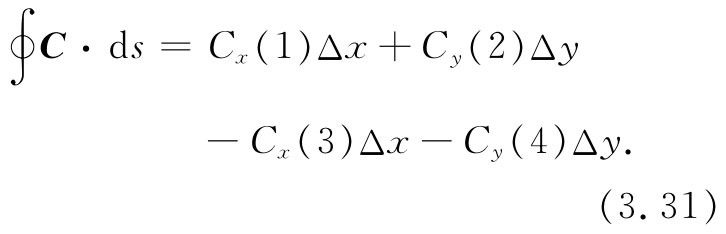
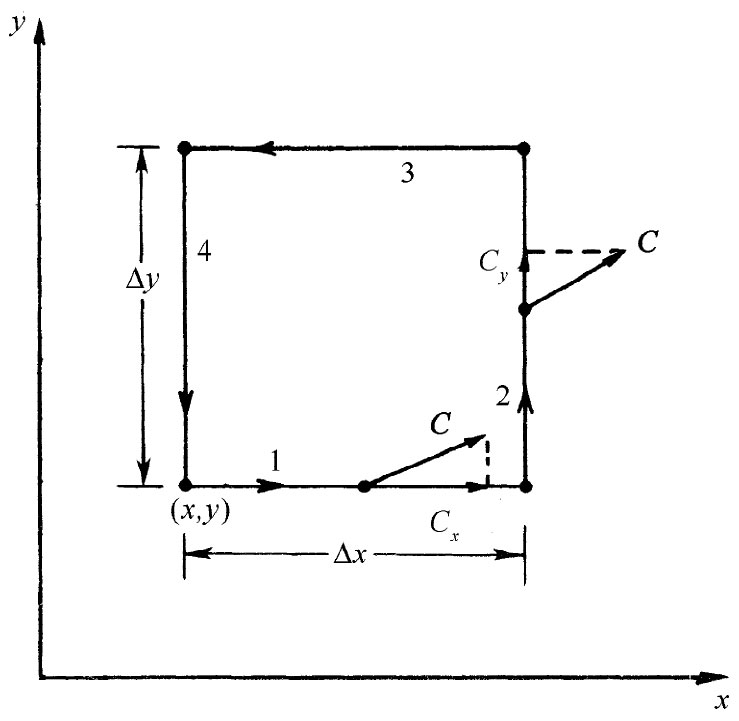
图3-10 计算绕行一个小正方形的C的环流
现在让我们注意第一和第三部分。它们合起来就是:
[Cx (1)-Cx (3)]Δx. (3.32)
你也许认为,对我们的近似程度来说这个差值为零。这对于一级近似是对的。然而可以更精确一些,计及Cx 的变化率。如果这样便可以写出:

假如把次级近似也包括进去,则会涉及到(Δy)2 等项,但由于我们最终将取Δy→0时的极限,所以这样的项都可以忽略。将式(3.33)和(3.32)结合起来,会得出
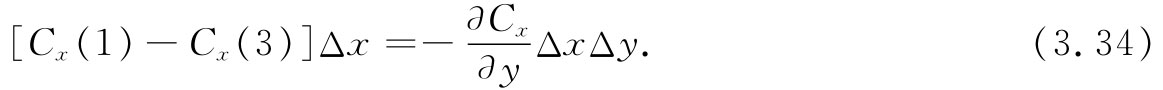
对于我们的近似,上式中的微商可以在(x,y)处计算出来。
同理,环流中的其他两项,也可以写成:
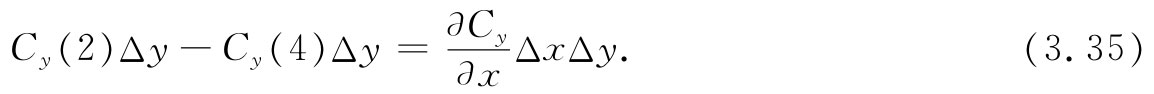
于是,绕上述那个小正方形的环流为:

这很有趣,因为括号内两项恰好就是旋度的z分量。并且,我们还注意到,ΔxΔy就是该正方形的面积。因此,可以将环流式(3.36)写为:
(▽×C)z Δa.
这个z分量实际上就是沿该表面元法向 的分量。因此,还可以将绕一个微分正方形的环流写成一种不变的矢量形式:
∮C·ds=(▽×C)n Δa=(▽×C)·nΔa. (3.37)
我们的结果是:任一矢量C绕一个无限小正方形的环流,等于C的旋度垂直于表面的分量乘以该正方形面积。
现在,绕任一条回路Γ的环流,可以轻而易举地同矢量场的旋度联系起来了。用任意合适的曲面S将回路填满,如图3-11所示,并把绕这个面上一系列无限小正方形的环流加起来。这个和可以写成一个积分。其结果是以斯托克斯命名(为纪念斯托克斯先生)的一个十分有用的定理。
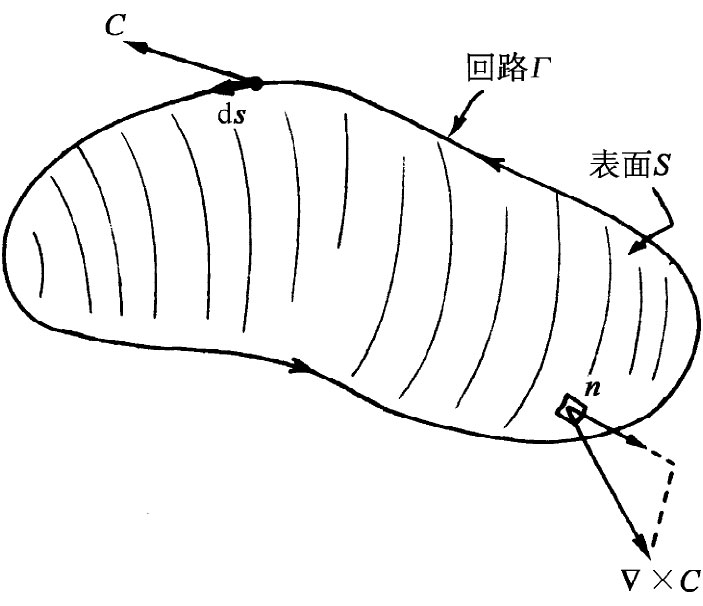
图3-11 C绕Γ的环流等于▽×C的法向分量的面积分
斯托克斯定理 :
∮Γ C·ds=∫S (▽×C)n da, (3.38)
式中S是以Γ为边界的任意曲面。
现在必须谈谈关于符号的一个惯例。在图3-10中,采用“常用”的——也即“右手”的——坐标系统,z轴将指向 你们。当按照旋转的“正”指向进行线积分时,我们发现环流等于▽×C的z分量。要是我们绕行的方向相反,即会获得一个相反的符号。那么,一般说来,我们怎么会知道应选取哪个方向作为▽×C的法向分量的正向呢?正法线始终必须与旋转的指向联系起来,如图3-10所示的。对于普遍情况,则如图3-11所示。
“右手法则”是记住这个关系的一种办法。如果你用右 手手指围绕曲线Γ,指尖指向ds的正方向,那么你的大拇指就指向S面的正 法线方向。