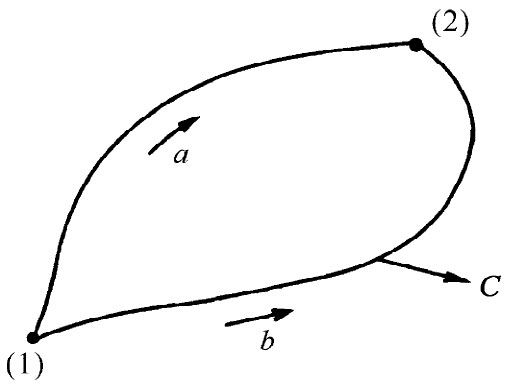
现在我们要来讨论上述新定理的某些结果。首先,考虑一个矢量其旋度处处 为零的情况。这时斯托克斯定理说,绕任何回路的环流等于零。现在若在一闭合曲线上选取两点(1)和(2)(图3-12),则从(1)至(2)的切向分量的线积分将与这两条可能路线中选取哪一条无关。我们可以断定,从(1)至(2)的积分只取决于这两点的位置——也就是说,它仅是位置的函数。同样的推理方法也曾在第1卷第14章中使用过,在那里我们曾证明如果某量绕一闭合回路的积分总是零,则该量对任一曲线的积分可以表达为两端点位置的某一函数之差。这一事实使我们创立了势的概念。而且,我们证明该矢量场就是这一势函数的梯度[见第1卷式(14.13)]。

图3-12 如果▽×C为零,则绕一闭合曲线Γ的环流等于零。从(1)至(2),C·ds沿a的线积分与沿b的线积分必相同
由此可见,任一旋度为零的矢量场等于某个标量函数的梯度。这就是说,如果处处▽×C=0,则存在某个ψ,使得C=▽ψ,这是一个有用的概念。如果愿意,我们可以用一个标量场来描述这一特殊类型的矢量场。
让我们再来证明另一件事。假设有任意的 标量场ϕ。如果取它的梯度即▽ϕ,那么这个矢量绕任意闭合回路的积分就必然为零。这矢量从点(1)至点(2)的线积分为[ϕ(2)-ϕ(1)]。如果(1)和(2)是同一点,那么定理1、即式(3.8)告诉我们,该线积分等于零:
∮回路 ▽ϕ·ds=0.
应用斯托克斯定理,我们可以得出结论:在任何曲面上
∫▽×(▽ϕ)n da=0.
但如果在任何 曲面上的积分都等于零,则该被积函数必定为零。所以,总有
▽×(▽ϕ)=0.
这个结果与我们在§2-7中应用矢量代数证明过的结果相同。
现在让我们考虑一种特殊情况,即用一个大 曲面S来填满一个小 回路Γ,如图3-13所示。实际上我们希望看看,当该回路缩小至一点、使得曲面的边缘消失不见而成为一闭合曲面时,究竟会发生什么情况。现在,如果矢量C处处有限,则当我们缩小该回路时,绕Γ的线积分应该趋于零——该积分大体上正比于Γ的周长,而周长趋于零。按照斯托克斯定理,(▽×C)n 的面积分也必为零。不知为什么,当我们把曲面关闭时,就会加进一些贡献将以前那里存在的东西抵消掉。因而我们得到一个新的定理:
∫任意闭合曲面 (▽×C)n da=0. (3.39)
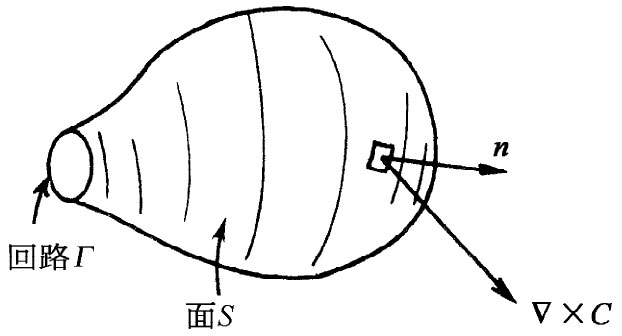
图3-13 在趋向于一个闭合曲面的极限上,我们发现(▽×C)n 的面积分必为零
这看来很有意思,因为我们已经有一个关于矢量场曲面积分的定理。按照高斯定理,即式(3.18),这样的面积分等于该矢量的散度的体积分。当应用于▽×C上时,高斯定理表明:
∫闭合曲面 (▽×C)n da=∫曲面内体积 ▽·(▽×C)dV. (3.40)
所以我们得出结论,第二个积分也应等于零,即
∫任意体积 ▽·(▽×C)dV=0, (3.41)
这对于任何矢量场C都正确。由于式(3.41)对于任何体积 都正确,所以在空间每一点 该被积函数为零就必然正确。因此,我们就恒有
▽·(▽×C)=0,
但这是§2-7中我们曾从矢量代数方面得到过的相同结果。现在我们开始来看看如何把每样东西配合起来。