
把式(4.5)和(4.6)作为我们的起点,照理应该是合乎逻辑的。然而,如从另外的某处出发再回到这些方程式上来,将会容易一些,而所得的结果是相同的。我们就从已谈及的那个被称为库仑定律的定律着手,它表明在两静止不动的电荷间有一个与这两个电荷之积成正比而与它们之间距离的平方成反比的力,这个力沿着从一电荷至另一电荷的直线。
库仑定律

F1 是作用于电荷q1 上的力;e12 是从q2 至q1 的方向上的单位矢量;而r12 则是q1 与q2 间的距离。作用于q2 上的力F2 与F1 大小相等而方向相反。
基于历史原因,比例常数写成1/4π∈0 。在我们采用的单位制——米·千克·秒(mkgs)制——中,它被定义为精确地等于10-7 乘光速平方。光速近似地等于3×108 ms-1 ,因此这个常数近似地为9×109 ,而其单位则可证明为Nm2 C-2 ,或者是VmC-1 。

单位:Nm2 C-2 或VmC-1 。
当存在两个以上的电荷时——唯一真正有意义的时候——我们就必须用自然界的另一事实来补充库仑定律。这个事实是:作用于任一电荷上的力等于其他每一电荷对它所施库仑力的矢量和。这个事实叫做“叠加原理”。这就是静电学所包含的全部内容了。如果把库仑定律和叠加原理结合起来,就不再有别的东西了。式(4.5)和(4.6)——静电学方程——正好包含这些。
应用库仑定律能很方便地引进电场的概念。我们说,场E(1)是作用于q1 上单位电荷 的力(由所有其他电荷所施)。对于除q1 外存在另一个电荷的情况,我们对式(4.9)除以q1 ,便得

此外我们还认为,即使q1 不存在,E(1)仍描述了有关点(1)的某些情况——假设所有其他电荷都保持其原有位置。我们讲:E(1)是点(1)处的电场。
电场E是一个矢量,因而式(4.11)实际指的是三个方程式——对于每一分量就是一个方程。把其中的x分量清楚地写出时,式(4.11)便意味着

其他分量均与此相仿。
如果有许多电荷,则在任意一点(1)处的场E就是其他每个电荷的贡献之和。这个总和中的每一项,看来都像式(4.11)或(4.12)。令qj 为第j个电荷的大小,而r1j 为从qj 至点(1)的位移,则可以写出
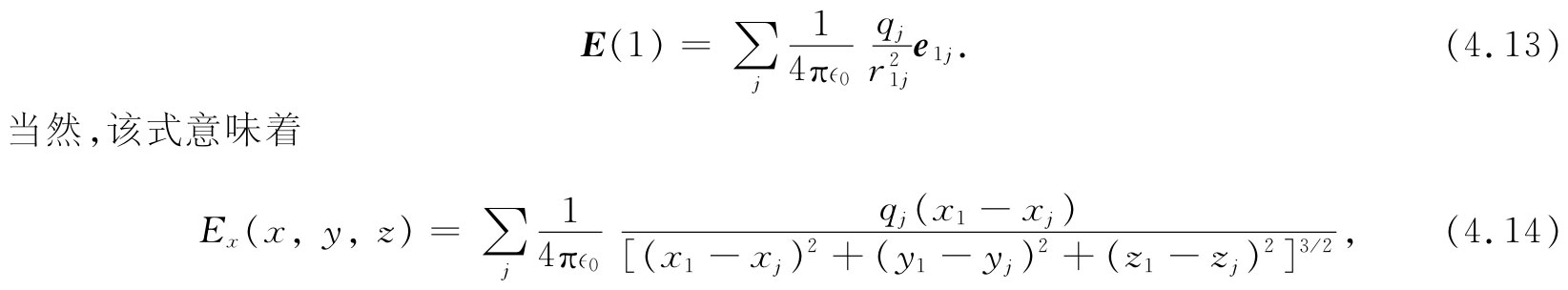
等等。
不把电荷看作像电子和质子那样的组成单元,而把它们想象成是铺展开的连续涂片或连续“分布”,往往会很方便。只要不去关注在尺度过小的范围内所发生的事情,这是可行的。这样,我们便可通过“电荷密度”ρ(x,y,z)来描述电荷分布。如果在点(2)处一个小体积ΔV2 内含有电量Δq2 ,则ρ便由下式定义
Δq2 =ρ(2)ΔV2 . (4.15)
为了将这种描述方法用到库仑定律上去,我们将式(4.13)、(4.14)中的那些求和,用对包含电荷的全部体积的积分来代替。这样就得到

有些人却喜欢写成
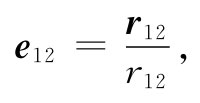
式中r12 是从(2)至(1) 的位移矢量,如图4-1所示。因此,对于E的积分就可以写成
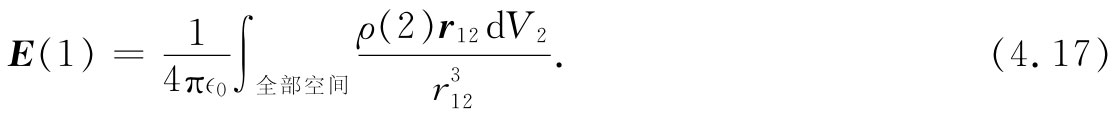
当我们要用这个积分进行具体计算时,通常还得详尽地把它写明白,对于式(4.16)或(4.17)的x分量,该写成
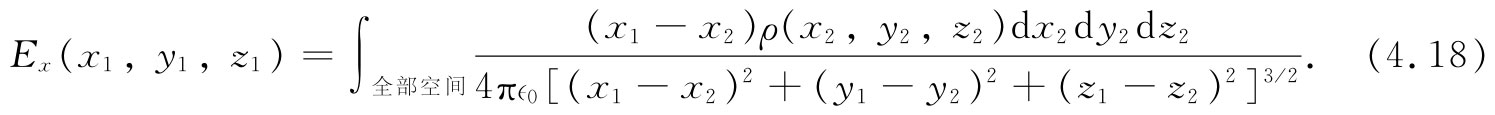
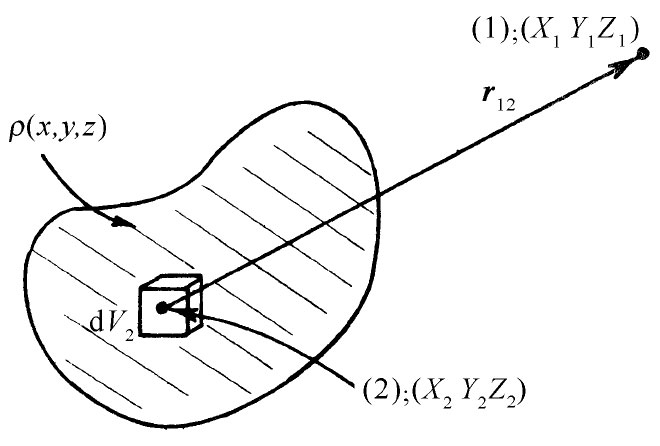
图4-1 分布电荷在点(1)处产生的电场E,可由对该分布的积分求得。点(1)也可以落在该分布区域之内
这个公式我们不会常用。之所以把它写在这里,只是为了强调,电荷位置都已知的所有静电学问题,我们已完全解决了。给定了电荷,场怎么样呢?答案 :算出这一积分。因此,对于这一课题便再没有什么可说了,那只是一个复杂的三维积分工作——严格说来,是一项计算机的工作!
借助这些积分,我们就能够求出各种电荷产生的场:面电荷、线电荷、球面电荷或任何特殊分布的电荷。重要的是要知道:当我们画场线、谈论电势或计算散度时,我们所有的答案都已在这里了。不过问题在于,有时某些聪明的猜测工作,比直接计算这个积分还要容易。这种猜测工作要求人们学习各种奇妙的东西。实践中,比较容易做的也许还是忘记追求聪明、总是直接而不是灵巧地把那些积分算出来。然而,我们打算尝试做得巧妙点。下面将继续讨论有关电场的某些其他特点。