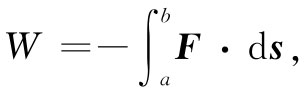
首先，我们讲讲电势的概念，它与电荷从一点移至另一点所做的功有关。设有某种电荷分布，产生了一电场。我们要问：如把一个小电荷从一处移至另一处需做多少功？沿某一路径移动电荷反抗 电力所做的功，等于这电力在运动方向分量的负 值沿该路径的积分。如果我们把一电荷从点a移至点b，则
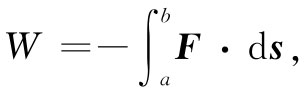
式中F是在每一点施于 电荷上的电力，而ds则是沿路径的微分位移矢量（见图4-2）。
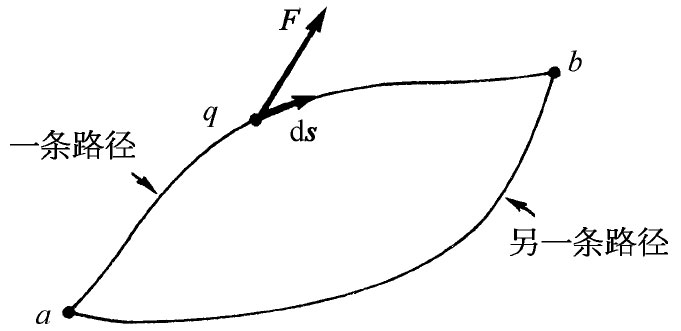
图4-2 把电荷从a移至b所做的功，等于F·ds沿所取路径进行积分的负值
对于我们来说，考虑移动一个单位 电荷所做的功会更有意义。因此，作用于电荷上的力在数值上就等于电场。在这种情况下反抗电力所做的功称为W（单位电荷），我们写为
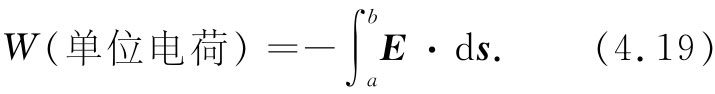
一般地说，用这类积分所得的结果与所取的路径有关。但是，假如式（4.19）的积分与从a至b的路径有关的话，那我们就可通过把电荷沿一条路径从a移至b、然后又沿另一条路径返回到a而从场中获得功。这样，可以沿W较小的那条路线达到b，而沿另一条路线返回 来，这样我们所得到 的功就会大于所付出 的功。
原则上说，从场中得到能量并不是不可能的。事实上，我们将遇到有这种可能的场。有可能当你移动电荷时，你就对这部“机器”的另一部分施加了力。若这部机器抵抗此力而运动，则它会损失能量，从而保持世界上的总能量不变。然而，对于静电学 来说，并没有这样一种“机器”存在，我们对反作用于场源上的力也很清楚，它们是作用于产生该场的那些电荷上的库仑力。如果其他电荷都固定在其位置上——这是静电学 中我们所做的唯一假设——这些反作用力就不能对它们做功，因而无法从它们那里获得能量——当然，这是以能量守恒原理对静电学的情况有效为条件的。我们相信它是有效的，请让我们证明，从力的库仑定律必然可以得出它来。
首先，考虑在一个起源于单个电荷q的场中所发生的情况。令点a与电荷q间的距离为ra ，而点b与q的距离为rb 。现在选择另一个大小为1个单位、称为“试验”电荷的电荷，从a移至b，我们开始用最简易的可能路径来计算。使试验电荷最初沿一圆弧、然后再沿某一半径移动，如图4-3（a）所示。求在这一条特殊路径所做之功，和小孩玩游戏一样简单（否则我们就不会选择这条路线了）。首先，在从a至a′的路径上根本没有做功。场是沿径向的（根据库仑定律），因而它与移动的方向成直角。其次，在从a′至b的路径上，场与移动方向相同，大小随1/r2 变化。于是，把试验电荷从a移至b所做之功应为
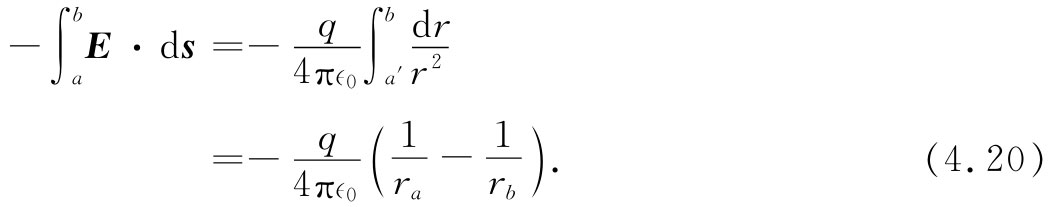
现在，再让我们取另一条简易路径。例如，取图4-3（b）所示的那条路径。它一会儿沿一圆弧，一会儿沿某一半径，然后又沿一圆弧，又沿一半径，等等。每次当我们沿圆周部分移动时，并没有做功。而当沿径向部分移动时，就只需对1/r2 积分。沿第一径向线段，我们从ra 积至ra′ ，然后沿第二径向线段，又从ra′ 积至ra″ ，如此等等。所有这些积分之和与直接从ra 至rb 的单一积分相同。对于这一路径所得答案与上面对第一条路径所得的一样。很清楚，对于任一条 由任意数目的同种线段构成的路径，我们将会得出相同答案。
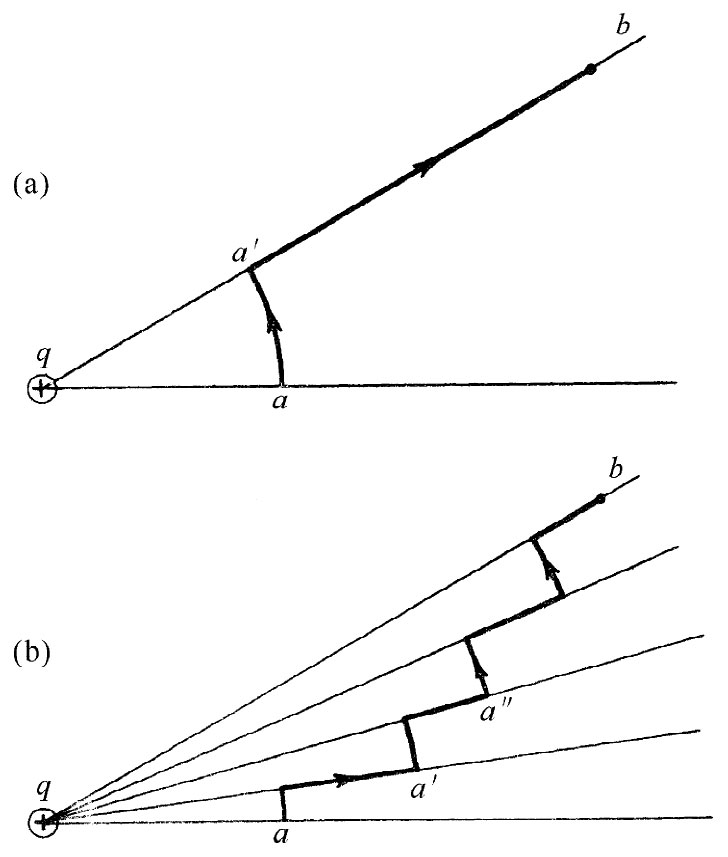
图4-3 把一试验电荷从a移至b时，无论沿哪一条路径所做的功都相等
若是一条光滑路径又将如何呢？会得出相同的答案来吗？在第1卷第13章中，我们就曾经讨论过这一点。应用与那里所用的相同论据，可以得出结论：把一单位电荷从a移至b所做的功应与所经历的路径无关，即
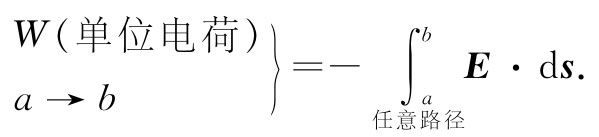
由于该功只与端点有关，所以它就可以表示为两个数值之差。我们可按下述办法看到这一点。试选定一参考点P0 ，并约定用一条总会经过 P0 点的路径来计算我们的积分。令ϕ（a）代表从 P0 至点a反抗场力所做的功，并令ϕ（b）为从 P0 至点b所做的功（图4-4）。这样，从a点（在去b的路上）至P0 点所做的功就会等于ϕ（a）的负值，所以我们有
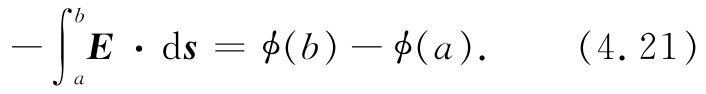
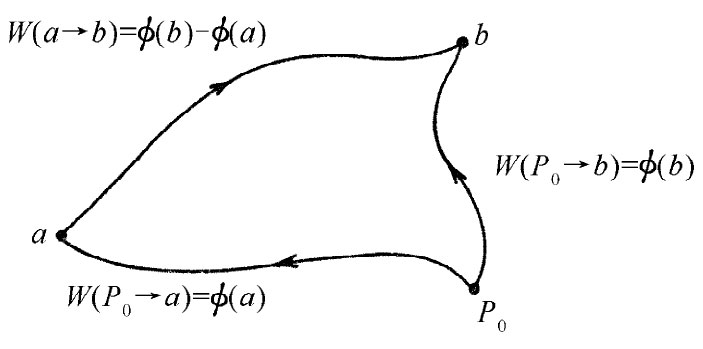
图4-4 沿任意路径从a至b所做的功，等于从某点P0 至a的功的负值加上从P0 点至b的功
由于所涉及的仅是函数ϕ在两点之差，所以我们实在没有必要去规定P0 的位置。然而，一旦我们选定了某个参考点，则就已确定了空间任一点 的一个数目ϕ。于是，ϕ就是一个标量场 ，它是x，y，z的函数。我们称这标量函数为在任一点的静电势 。
静电势
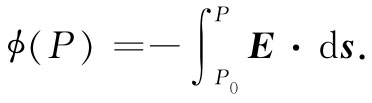（4.22）
为了方便，我们常把参考点选在无限远。于是，对于位于原点的单个电荷来说，应用式（4.20），任意点（x，y，z）处的势ϕ为
若干个电荷所产生的电场，可写为第一个、第二个、第三个等等电荷所产生的电场之和。当对和进行积分以求电势时，我们便得到一些积分之和。其中每个积分就是一个电荷所产生的势的负值。我们断定，许多电荷所产生的势ϕ等于所有各个电荷所产生的势之和。这也就是势的叠加原理，应用过去求一群电荷或分布电荷的电场的相同论据，就可得出称为点（1）处电势的完整公式：
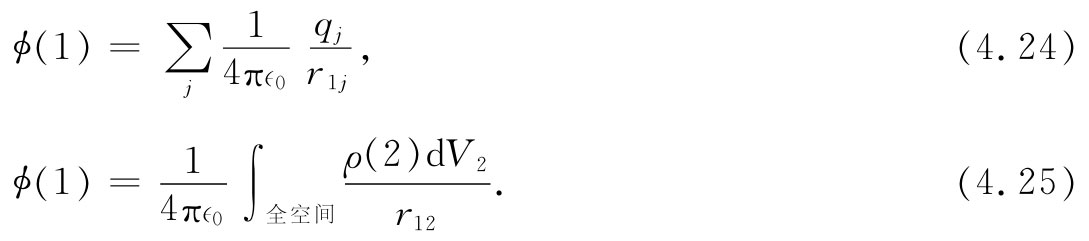
记住势ϕ的物理意义：它是单位电荷在空间从某个参考点被移至指定点时所具有的势能。