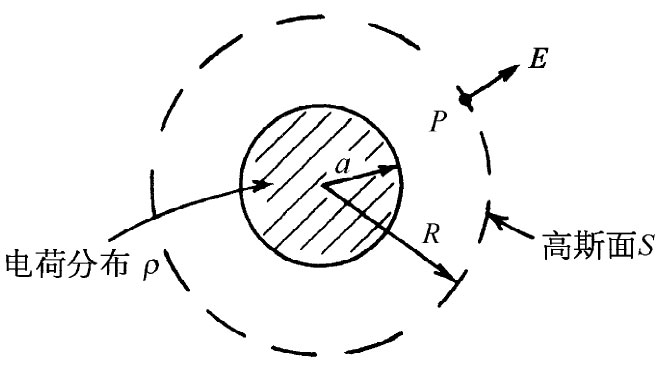
图4-11 应用高斯定律求一个均匀带电球体的场
过去我们学习引力吸引理论时，遇到的困难问题之一就是要证明：一个实心球体物体所产生的力，与所有物质都集中在其中心或位于球面所产生的力是相同的。牛顿经过了许多年都没有把他的引力理论公诸于世，就是因为他当时还不敢肯定这个定理是正确的。我们在第1卷第13章中，曾经通过算出关于势的积分，然后利用梯度求得引力来证明这个定理。现在，我们能够用最简单的方式来证明它，只是这次将证明关于一个均匀带电球体的相应定理（由于静电学定律与引力定律相同，所以同样的证法也可用于引力场）。
图4-11 应用高斯定律求一个均匀带电球体的场
我们要问，在一个充满均匀分布电荷的球体外面任一点P处的电场E是什么？既然不存在“特殊”的方向，我们便可以假定E处处都是从球心向外。考虑一个与该带电球体同心的、并通过P点的球面（图4-11）。对于这个面，向外通量为
∫En da=E·4πR2 .
高斯定律告诉我们，这一通量等于该带电球体的总电荷Q（除以∈0 ）：
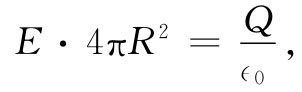
或
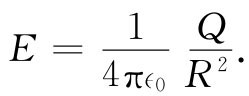（4.39）
这与一个点电荷Q的公式相同。我们比求积分更容易地证明了牛顿的问题。当然，这种容易是不真实的——由于你已花了某些时间才能理解高斯定律，所以你也可以认为实际上没有节省时间。但是当你越来越多地应用这一定理以后，便会开始有所收获。这是一个效率问题。