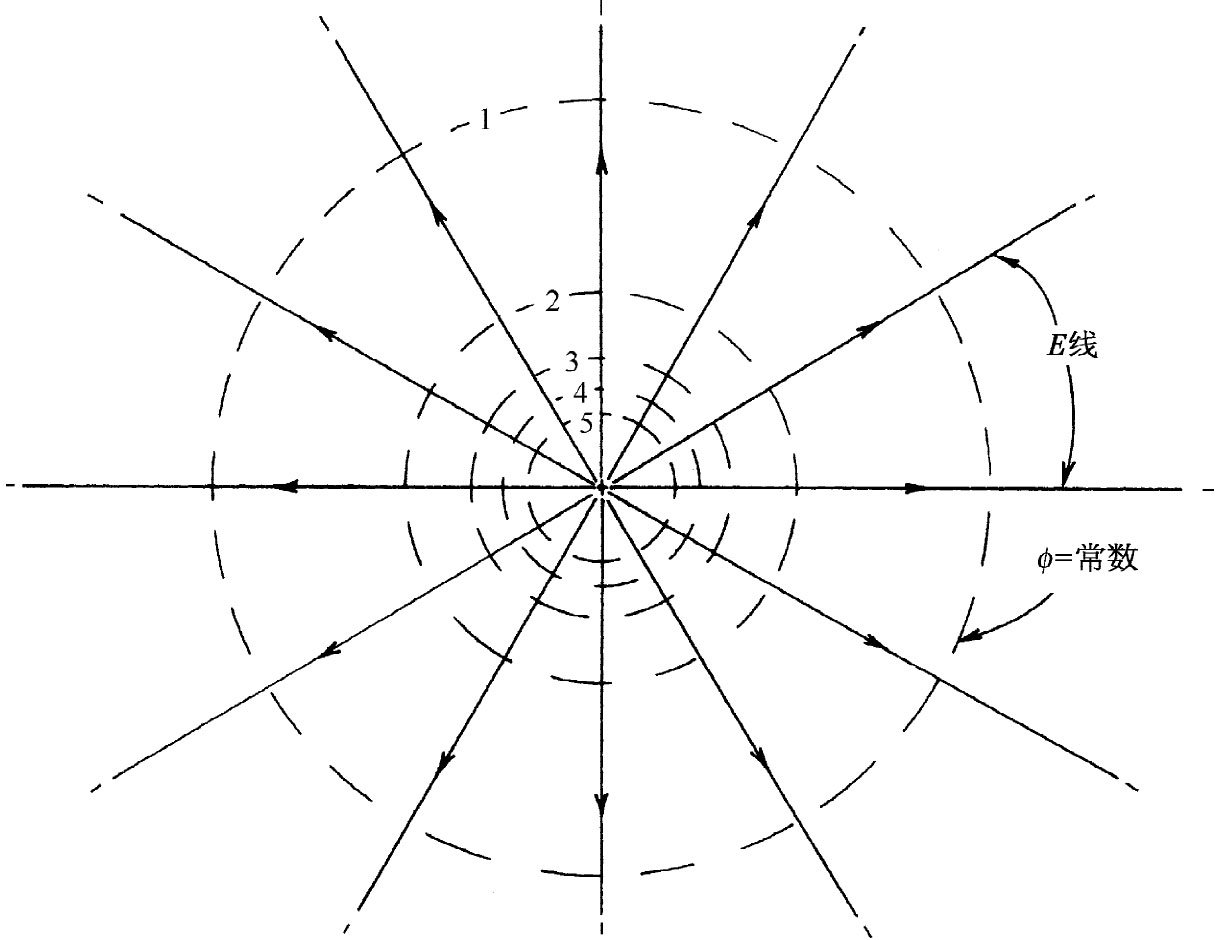
图4-12 一个正点电荷的场线和等势面
现在,我们想要给出静电场的一种几何描述。静电学的两定律,一个为通量正比于内部电荷,另一个表明电场是势的梯度,它们也可以用几何方法来表示。下面用两个例子来说明。
首先,我们取一个点电荷的场为例。在场方向画线——总是与场相切的线,如图4-12所示。这些线称为场线 ,它们处处指明电矢量的方向。但我们还希望表达出该矢量的大小。为此,我们可以制定这样的规则:电场强度将由场线的“密度”表示。所谓场线的密度,是指通过与该线垂直的单位面积的线的数目。应用这两条规则就可以得出一幅电场图像。对于一个点电荷来说,场线的密度必须按1/r2 减少。但在任何半径r处与线垂直的球面面积却会随r2 而增大 ,所以如果对于离电荷的一切 距离处我们都保持线的数目相同,则密度 将保持与场的大小成正比。只要我们坚持所画出来的线是连续 的——即一旦线已从电荷发出,它就永远不会停止,那么,我们就能保证在每个距离处线的数目都相同。依赖场线,高斯定律说,这些线只应从正电荷出发而终止于负电荷。离开 电荷q的线的数目一定等于q/∈0 。

图4-12 一个正点电荷的场线和等势面
现在,对于势ϕ来说,我们也能找到一个相似的几何图像。表达势最方便的方法是画出ϕ为常数的那些面。这种面称为等势面 ——势相等的面。那么,等势面与场线间的几何关系又是如何呢?电场是势的梯度。梯度是在势变化最迅速的那个方向,所以它垂直于等势面。假如E并不 垂直于这种面,那么它会有一个沿 面分量。此时,势会在面上发生变化,于是该面就不会是等势的了。因此,等势面必然会处处与电场线成直角。
对于一个孤立的点电荷来说,等势面是以该电荷为中心的球面。我们已在图4-12中显示出这些球面与一个通过该电荷的平面的交线。
作为第二个例子,我们考虑在两个大小相等而符号相反的电荷附近的场。要获得这个场挺容易。总场由该两电荷各自的场叠加而成。因此,我们可以取两幅如4-12那样的图并把它们叠加起来——不可能!这样我们会有彼此相交的场线,而这是不可能的,因为E不能在同一点上有两个方向 。场线图的缺点现在就显而易见了。根据几何论证不可能用十分简单的方法去分析那些新场线的去向。从两个独立图像我们不能获得一个综合的图像。叠加原理固然是关于静电场的一个简单而又深刻的原则,但在场线的图像方面,还没有一个容易的表达方式。
关于单位的备忘录

然而,场线图形毕竟有它的用途,所以对于一对相等(而相反的)电荷我们也许仍乐于去画出其图像来。若我们由式(4.13)算出场,又由式(4.24)算出势,那么,便可描绘出场线和等势面。图4-13显示这个结果。但我们得先在数学上解决这个问题!
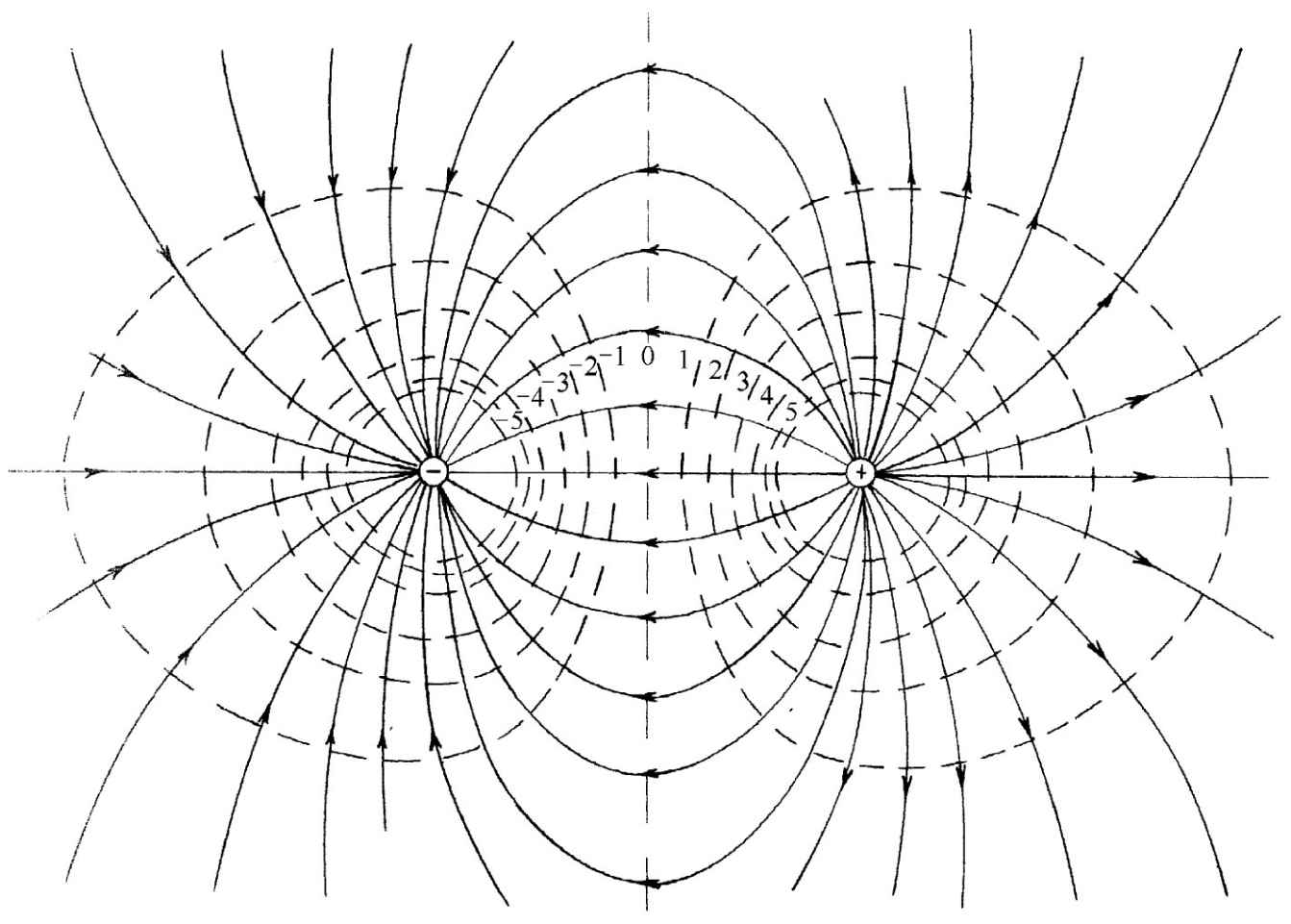
图4-13 两个相等而相反的点电荷的场线和等势面