首先,考虑下述问题:一个处于其他电荷的电场中的点电荷何时才能处于稳定的力学平衡状态呢?作为一个例子,试设想在一水平面上有一个等边三角形,在每个角上各放置一负电荷。一个置于该三角形中心处的正电荷是否会保持在那里(如果暂时略去重力,问题就会简单些,尽管把它包括进去也不会改变所得结果)?作用于该正电荷上的力为零,但这个平衡稳定吗?要是稍微移动一下电荷,它会回到平衡位置上来吗?答案是否定的。
在任何 静电场中都不会有 稳定的平衡点——除非这一点恰好叠在一个电荷上。应用高斯定律很容易看出其原因。首先,要使电荷在任一特定P0 点上处于平衡,场就必须等于零。其次,如果平衡是一稳定平衡,则还要求若把电荷沿任一 方向移离P0 点,便应有一个与位移反向的恢复力。在一切 邻近点的电场都必须指向内——即指向P0 点。但如果在P0 点没有电荷存在,那就会违反高斯定律,这点我们可以很容易看出来。
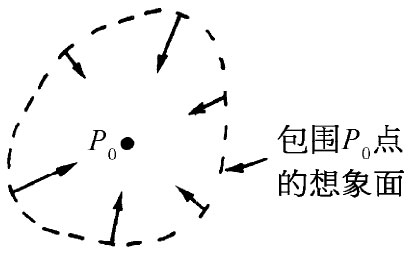
考虑一个包围着P0 点的小想象面,如图5-1所示。若在P0 点附近的电场处处都指向它,则对场的法向分量的面积分就肯定不会等于零。在上图所示的情况中,通过该面的通量必然是一负值。但高斯定律说明,通过任何曲面的电场通量正比于在该面内的总电荷。如果在P0 点处没有电荷,则我们想象出来的场便违反了高斯定律。在一个空的空间里,在那里的某一点不存在一些负电荷,使位于该点的一个正电荷处于平衡是不可能的。如果一个正电荷处于某一分布的负电荷中间,则它可以 达到平衡。当然,那些负电荷的分布就必须由电力以外的力把它们固定在适当的位置上!

图5-1 如P0 对于一个正电荷来说是一个稳定平衡点,那么在其附近每一处的电场就都应指向P0 点
对于一个点电荷我们得到了上述结果。这同一结论是否也适用于被固定——比如用棍子来固定——在相对位置上分布复杂的电荷呢?我们考虑关于固定在一条棍子上的两个相等电荷的问题。这个组合在某个静电场中能否处于平衡呢?答案再次是否定的。因为作用于棍子上的总 力不可能对于每一方向上的位移都具有恢复作用。
设作用于棍子上任意位置的总力为F——因此,F就是一个矢量场。根据上面所用的论据,我们断定:在一个稳定平衡的位置上,F的散度必定是一个负值。但作用于棍子上的总力则等于第一个电荷乘以在其位置上的电场,加上第二个电荷乘以在其位置上的电场:
F=q1 E1 +q2 E2 . (5.1)
F之散度为 ▽·F=q1 (▽·E1 )+q2 (▽·E2 ).
倘若q1 和q2 两电荷中每一个都处在自由空间里,则▽·E1 和▽·E2 均等于零,因而▽·F也就等于零——不是负值,而负值是对于平衡所要求的。可以看到,这论证的引申表明:在自由空间的静电场中,由任意数目电荷的刚性组合都不可能有一个稳定的平衡位置。
我们至今没有证明,即使有一些支点或其他机械约束,平衡仍然是不可能的。作为一个例子,考虑一根空心管,其中有一电荷可以自由往复运动,但却不能向旁移动。现在,不难设计出这么一个电场:在管两端处场都指向内,而容许在管中心附近场可以从管侧面指向外。我们只要将正电荷置于管的两端,如图5-2所示。眼下虽然E的散度仍等于零,但可能有一个平衡点。当然,假如不是由于从管壁所加的“非电”力,则该电荷对于侧向运动来说还是不会处于稳定平衡的。
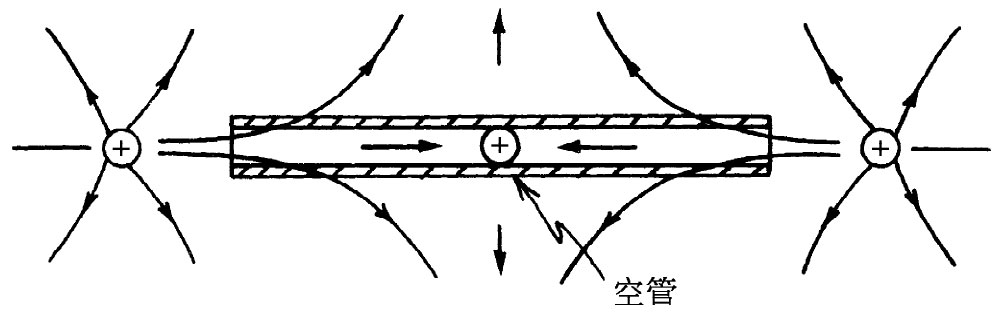
图5-2 如果有一些机械约束,电荷就可处于平衡