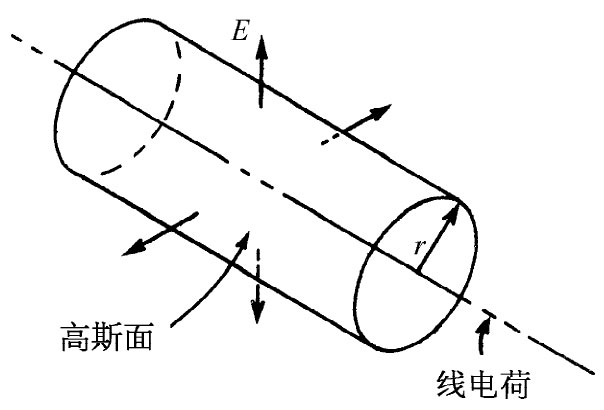
图5-5 与线电荷同轴的一个圆柱形高斯面
高斯定律可以用来解决许多其中包括某种特殊对称性——通常是球形、圆柱形或平面形的对称性——的静电场问题。在本章的剩下部分,我们将用高斯定律来处理几个这样的问题。应用高斯定律很容易解决这些问题,这可能会引起一种错误印象,以为这种方法非常有效,人们将能够继续用它去对付其他许多问题。可惜情况并非如此。人们很快就搜索尽能够用高斯定律容易加以解决的问题。在以后几章中,我们将发展一些研究静电场的更强有力的方法。
作为第一个例子,我们考虑一个具有圆柱形对称性的系统。假设有一根十分长而均匀带电的棒,电荷沿一无限长直线均匀地分布着,单位长度所带的电荷为λ,我们希望知道电场。当然,问题可以通过对来自线的每一部分对场的贡献进行积分而加以解决。但我们准备不用积分,而通过应用高斯定律以及某种推测来求解。首先,推测该电场会从直线径向地向外。这是因为,从线中一边的电荷所产生的场的任何轴向分量,将伴随着从线的另一边电荷产生的场的相等的轴向分量,结果就只能为径向场。在与直线等距离的所有各点上,场应有相同大小,这似乎也是合理的,而且很明显(这一点可能不容易证明,但如果空间是对称的——正如我们所确信的那样——则它便是正确的)。

图5-5 与线电荷同轴的一个圆柱形高斯面
我们可按下述方式来应用高斯定律。考虑一个与该线同轴的圆柱形假想 曲面,如图5-5所示。按照高斯定律,从这一个面出来的E的总通量等于其内部电荷除以∈0 。由于场假定是垂直于该面的,所以其法向分量就是场的大小,叫作E。令该柱面的半径为r,为了方便起见其长度取为一个单位。通过该柱面的通量等于E乘以该面面积(即2πr)。因为电场与之相切,通过两个端面的通量等于零. 因为在其中的线长为一单位,在该曲面之内总电荷恰好是λ. 于是高斯定律给出

线电荷的电场与从线至该处的距离的一次 幂成反比。