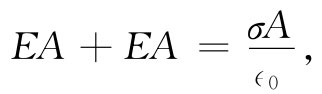
作为另一个例子,我们现在来计算均匀面电荷所产生的场。假设该面延伸至无限远,而且单位面积的电荷为σ。我们要做一种推测:考虑到对称性,我们相信场的方向处处与该平面垂直,而倘若没有来自世界上任何其他电荷的场 ,则两边的场(大小)应相等。这次我们选取的高斯面是一个穿过该平面的四方盒子,如图5-6所示。平行于该平面的两个表面面积相等,比如说A。场垂直于此两面,而与其他的四个面平行。总通量等于E乘以第一个面的面积,加上E乘以其对面的面积——其他四个面都没有做任何贡献。包含在该盒子里的总电荷为σA。使通量与其内部电荷相等,我们便有
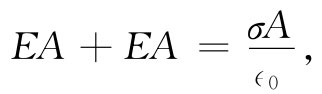
由此得
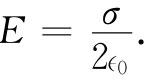 (5.3)
(5.3)
这是一个简单而又重要的结果。
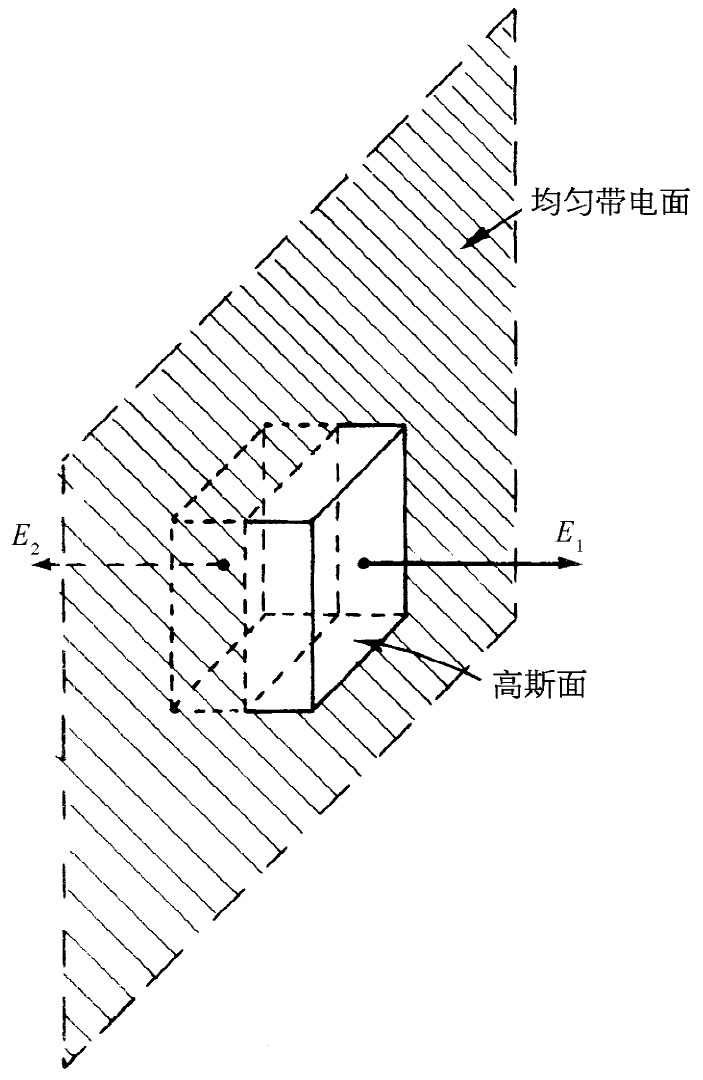
图5-6 在一均匀带电面附近的电场,可通过应用高斯定律于一个想象的盒子而求得
你或许记得,这同样的结果曾在前面一章中通过对整个面进行积分而获得。在这个例子中,高斯定律更迅速地给出了答案(虽则它并不如以前的方法那么普遍适用)。
必须强调,这一结果仅 适用于面电荷的场。如果在面电荷附近还有别的电荷,则靠近该面的总场就应等于式(5.3)与其他电荷的场之和。此时,高斯定律只会告诉我们:
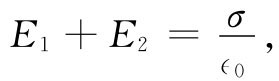 (5.4)
(5.4)
式中E1 和E2 分别代表从该面每侧指向外之场。
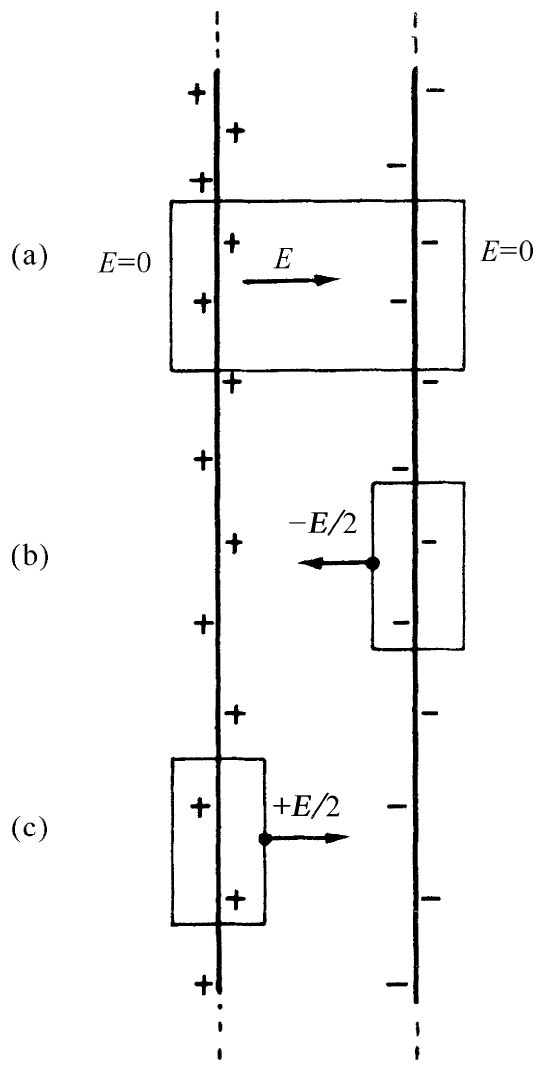
图5-7 两块带电板之间的场为σ/∈0
只要我们再次假定其外部世界是对称的,带有相等相反电荷(密度分别为+σ和-σ)的两平行板问题也同样简单. 通过对由单块板所得的两结果叠加,或者通过构成一个包括两板在内的高斯盒,都不难见到,在该两板之外 的电场为零[图5-7(a)]。由考虑一个只包括这块或那块板在内的盒,如图5-7(b)或(c)所示的那样,则能看出两板间的场应两倍于单独一块板的场。结果是:
E(在两板之间)=σ/∈0 ; (5.5)
E(在两板之外)=0. (5.6)