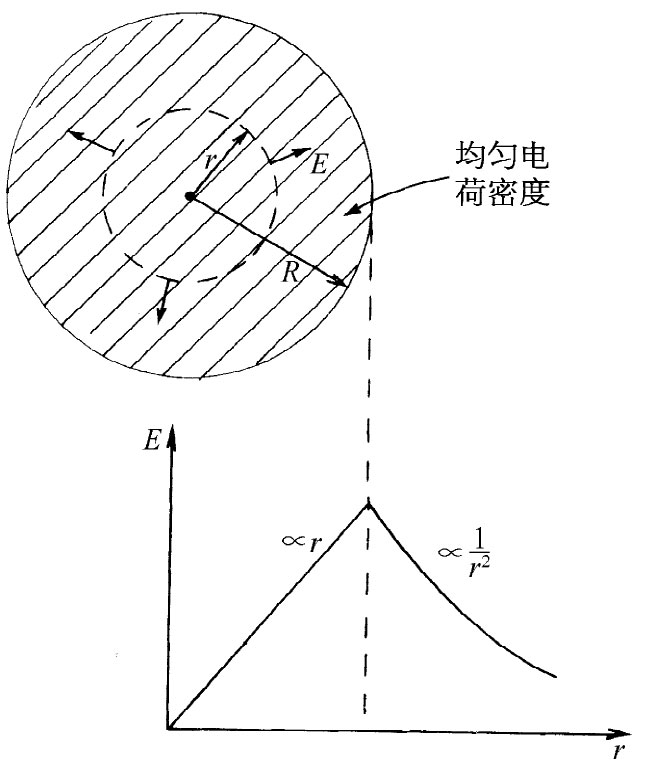
图5-8 高斯定律可用来求一个均匀带电球体内的场
我们曾(在第4章中)应用高斯定律求得一个均匀带电球体外的场。用同一方法也能给出球内 各点的场。例如,这种计算方法可用来得到对原子核内部场的良好近似。尽管核里的质子互相排斥,但由于强大核力的作用,它们还是几乎均匀地分布在核体内的。

图5-8 高斯定律可用来求一个均匀带电球体内的场
假设有一个半径为R并均匀地充满着电荷的球,令ρ为单位体积的电荷。再利用对称性的论证,假定场是径向的,并且在与球心等距离的一切点上这个场的大小都相等。要求与球心的距离为r处的场,我们取一个半径为r(r<R)的球形高斯面,如图5-8所示。从这个面出来的通量为
4πr2 E.
在我们的高斯面内的电荷等于其内部体积乘ρ,或
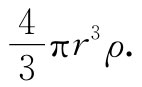
应用高斯定律,可以推得场的大小由下式给出:
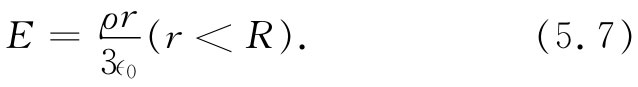
你可以看到,这一公式对于r=R也会给出恰当的结果。电场与半径成正比 ,并沿径向指向外。
刚才对于一个均匀带电球体所提供的论证,也可应用于一个带电薄球壳。假定场是处处径向的并且具有球对称性,那便可以立即从高斯定律获得在球壳外的场与一个点电荷的场相似,而球壳内的场则处处为零(在球壳内的高斯面将不会包含电荷)。