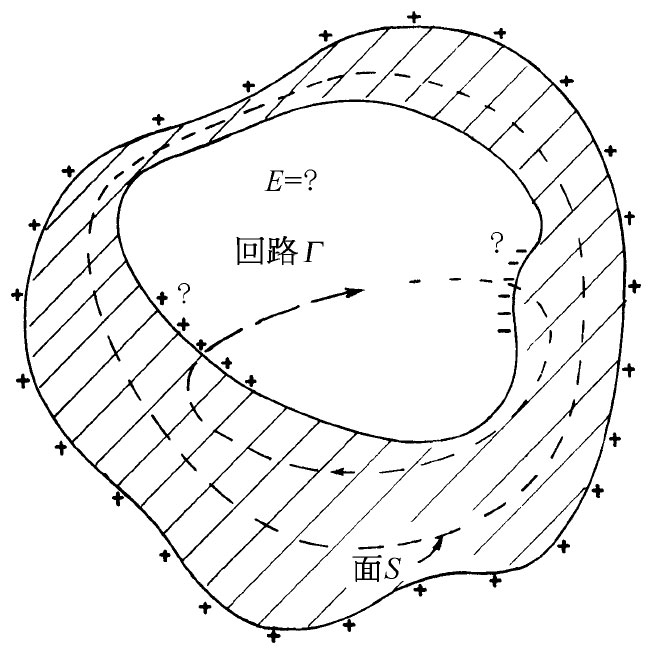
图5-12 在一个任意形状的导体空腔里其电场如何
现在,我们转到一个中空容器——导体内留有空腔——的问题。虽然在金属 中不存在场,但在其空腔 里怎样呢?我们将证明:如果空腔是空 的,则不管导体或空腔的形状如何 ——比方说如图5-12所示的那种形状——在其中不存在场。考虑一个高斯面,像图5-12中的S,它包围着该空腔,但还处处落在导电材料之内。由于在S上的任何地方场均为零,所以并没有通量通过S面,因而在S面内的总 电荷等于零。对于一个球壳来说,人们可以从对称性论证其内部没有 电荷。但在一般情况下,我们只能说在导体的内表面上存在等量的正电荷与负电荷。即可能 其中一部分内表面存在正的面电荷而另一部分存在负的面电荷,如图5-12所指出的那样。高斯定律并不能排除这种情况。

图5-12 在一个任意形状的导体空腔里其电场如何
当然,实际发生的情形是,任何在内表面上出现的等量异号电荷都会向四周滑动而彼此相遇,从而完全抵消掉。我们可通过应用E之环流始终等于零这个(静电学)定律来证明,它们必定完全抵消掉。假定在内表面的某些部分上存在电荷,则我们知道,在其他地方也得有与之数目相等而符号相反的电荷。那么任何E线就必须从那些正电荷出发而终止于那些负电荷上(因为我们所考虑的只是在空腔里并没有自由电荷的那种情况)。现在设想有这么一条回路Γ,它沿一条从某一正电荷至某一负电荷的力线穿过空腔,并经由导体回到原来的出发点(如图5-12所示)。沿这条力线从正电荷至负电荷所取的积分不会等于零。而经过金属里的积分则为零,因为E=0. 因此,我们就应该有
∮E·ds≠0???
但在静电场中,E绕任一闭合回路的线积分总是为零。因此,在空腔里不可能存在任何场,而在内表面上也不会有任何电荷。
应当仔细地注意我们所做出的一个重要限制条件。上面我们总是说在一个“空 的腔里”,但如果有某些电荷被置 于腔里的某些固定位置上——诸如被置在一个绝缘体上或一个与该主导体绝缘的小导体上——那么腔里就可以 有场,但此时这个腔已经不是“空”的了。
我们已经证明:如果一个空腔给导体完全包围住,则任何外部 静止的电荷分布都不可能在其内部产生出任何场。这说明了通过将电学设备放在一个金属盒内就能把它们“屏蔽”起来的原理。同样某些论证也可用来证明,在一导体闭合面内部 的任何静电荷分布不可能在其外部 产生出任何场。屏蔽对双方都有效!在静电学中——但不是在变化着的场中——一个闭合导体壳两边的场是完全独立的。
现在你明白,为什么以往在核对库仑定律时能够达到那么高的精度。所用空壳的形状是无关重要的,并不一定是球形,立方的也可以!如果高斯定律严格正确,则里面的场始终为零。现在你也懂得,为什么坐在那百万伏范德格拉夫起电机的高压套管内可以安然无恙,并不必担心会受到电击——这是由于高斯定律的缘故。