
本章将描述在几种不同情况下电场的行为。它将向我们提供有关电场表现方式的一些经验,并将描述求解这种电场的某些数学方法。
首先我们要指出,全部数学问题在于解静电学的两个麦克斯韦方程:

实际上,上述两方程也可合并成一个方程。从第二个方程我们立即知道可以把场描述为标量的梯度(见§3-7):
E=-▽ϕ. (6.3)
如果我们乐意,就可以用势ϕ完整地描写任一个特定电场。将式(6.3)代入式(6.1)中,便可得到ϕ所应服从的微分方程
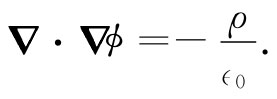 (6.4)
(6.4)
ϕ梯度的散度与用▽2 对ϕ进行运算的结果相同,即
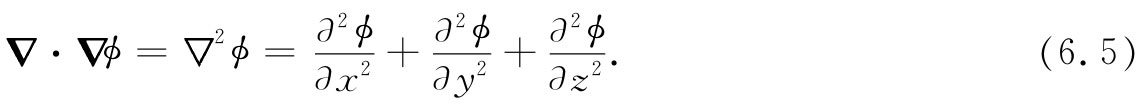
因此,我们便可将式(6.4)写成
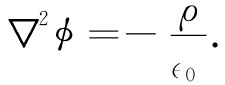 (6.6)
(6.6)
算符▽2 称为拉普拉斯算符,而式(6.6)则称为泊松方程。从数学的观点看,静电学整个课题只不过是学习这一方程式(6.6)的解。一旦ϕ由解方程式(6.6)得出,便可立即由式(6.3)求得E。
我们将首先提出其中ρ作为x,y,z的函数是已知的那种特殊类型的问题。在这种情况下问题几乎是琐碎肤浅的,因为我们已知道式(6.6)的一般解了。以前就曾证明过:若ρ在每点均为已知,则在点(1)处的势就是

式中ρ(2)和dV2 分别代表点(2)处的电荷密度和体积元,而r12 则为(1)与(2)两点间的距离。微分 方程式(6.6)的解已简化成对整个空间的积分 。式(6.7)这种解应加以特别注意,因为物理学中就有许多情况都会引导到如
▽2 (某件东西)=(另一件东西)
这样一种方程,而式(6.7)便是任何这类问题解的典型。
这样,当所有电荷的位置都已知时,静电场问题的解就完全是直截了当的。让我们在下述几个例子中看看这是怎么回事吧!