§6-2　电偶极子

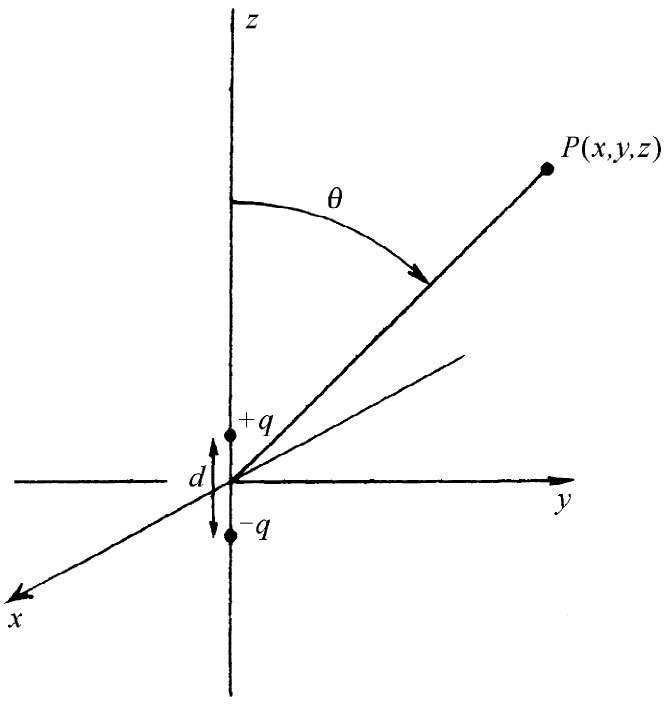
图6-1　偶极子：相距为d的两个电荷+q和-q

首先，取相距为d的两个点电荷+q和-q。令z轴沿这两电荷的连线，并选取原点在其中间，如图6-1所示。于是，应用式（4.24），则来自这两电荷的势就是

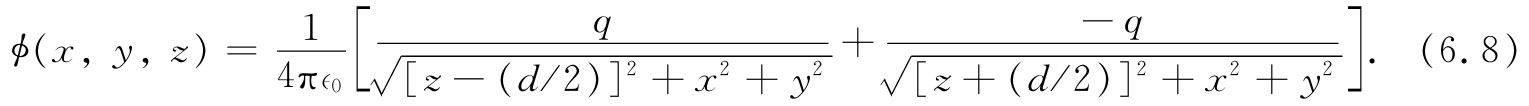
我们不打算把电场的公式写出，因一旦已有了势，就总可以把场算出来。因此，我们已解决了两电荷的问题。

存在两电荷靠得非常近的一种重要特殊情况——即是说，我们所感兴趣的仅仅是在与这两电荷的距离远比它们的间距为大的那些地方的场。我们称这样靠近的一对电荷为偶极子 。偶极子是十分常见的。

例如，“偶极”天线常用互相分开一小段距离的两电荷来做近似——如果我们不去过问太接近于天线地方的场的话（我们经常对带有运动 电荷的天线感兴趣，但这里静电学方程组实际上已不适用了。对于某些目的来说，那还是足够近似的）。

也许更重要的还是原子偶极子。在任何材料中，如果有一电场存在，则电子和质子将感受到方向相反的力并做相对移动。你会记起，导体中有些电子会移向表面，使内部的场变为零。在绝缘体中，电子不能够移得很远，它们将被核吸引回来。然而，它们的确会移动一点点。因此，尽管一个原子或分子在一外加电场中仍然保持中性，但它的正电荷和负电荷间会出现一个十分微小的间隔，从而成为一个微观的电偶极子。如果我们所感兴趣的是这些原子偶极子在普通大小物体附近的场，那么，我们正在与比这些电荷对的间隔大得多的距离正常地打交道。

在某些分子中，即使没有外电场存在，电荷也还是有点分开，这是由于分子的形状所致。例如，在一水分子中，氧原子附近有净负电荷，而两个氢原子附近则都有净正电荷，它们并非对称地排列着，而是如图6-2所示。尽管整个分子的电荷为零，但却形成这样一种分布：在一方有稍微多一点的负电荷而在另一方则有稍微多一点的正电荷。这种排列肯定不会像两个点电荷那么简单，但从远处看时，这个系统的作用就像一个偶极子一样。正如稍后我们便将见到的，在远距离处场对于这种细节并不敏感。

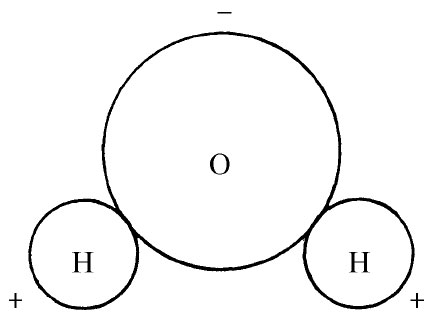
图6-2　水分子H2 O。两个氢原子各拥有稍微少于其份额的电子云；氧原子则稍微多些

那么，就让我们来看看，具有小间距d的两个异号电荷所产生的场。如果d变为零，两电荷互相重叠，两势则互相抵消，因而也就没有场了。但如果它们并不严格互相重叠，那就可通过将式（6.8）中各项（应用二项式展开法）展开成小量d的幂级数，从而可以得到势的一个优良近似。若仅仅保留d的一级项，便可以写成

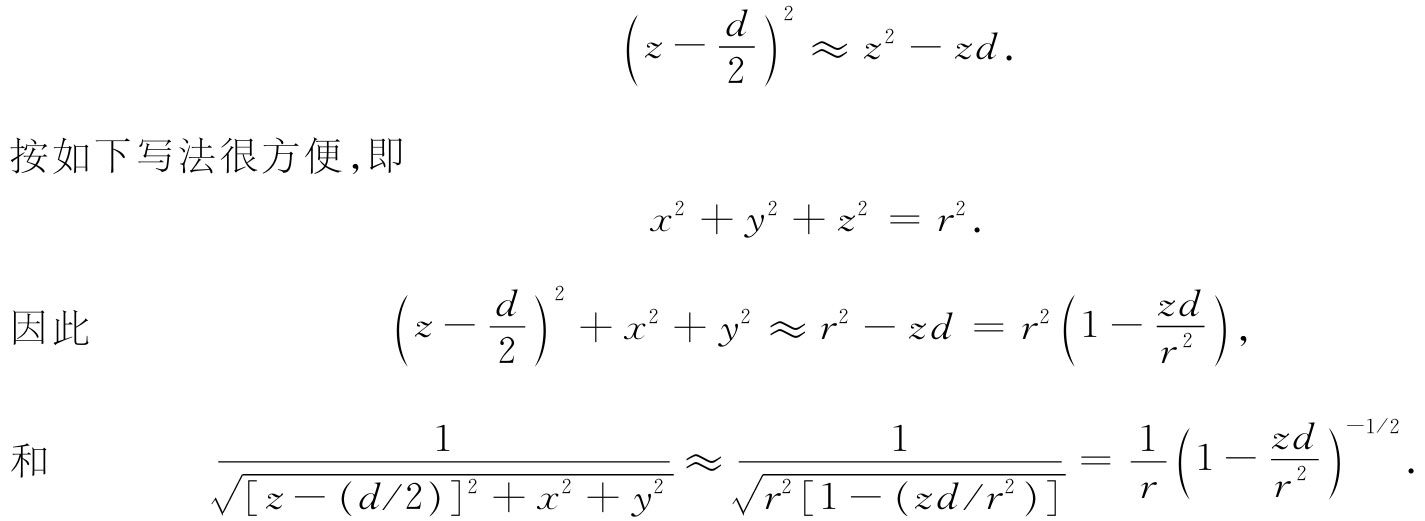
对于［1-（zd/r2 ）］-1/2 ，可再应用二项式展开——并丢掉d的平方及更高幂次的项——我们便得

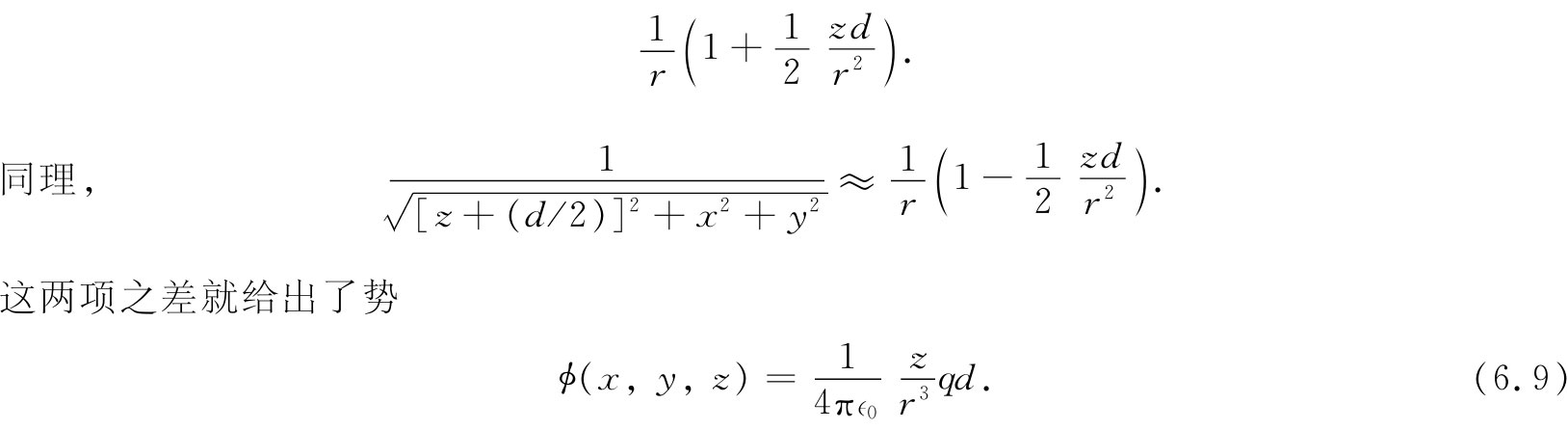
得到这个势，也就有了电场（那是势的微商），它们都会正比于qd，即电荷与间距的乘积。这个积被定义为这两个电荷的偶极矩 ，我们用符号p（切勿 与动量混淆！）表示，即

p=qd.　（6.10）

式（6.9）也可写成

因为z/r=cosθ，其中θ是偶极子轴与指向点（x，y，z）的径向矢量之间的夹角——见图6-1。在对轴给定的方向上，偶极子的势 按1/r2 下降（但对于一个点电荷，则按1/r下降）。于是偶极子的电场E便会按1/r3 减弱。

如果定义一个大小为p、方向沿偶极子轴从-q指向+q的矢量p，则我们可把上式写成矢量形式。这样，

pcosθ=p·er ，　（6.12）

式中er 为单位径向矢量（图6-3）。我们也可用r代表点（x，y，z）。于是

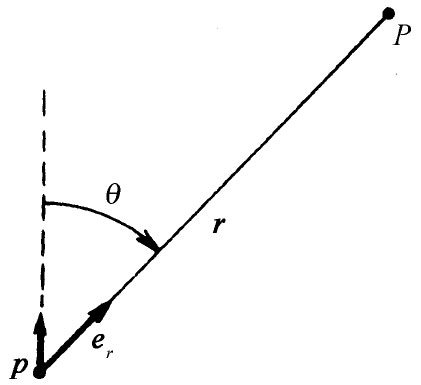
图6-3　电偶极子的矢量符号

偶极子势

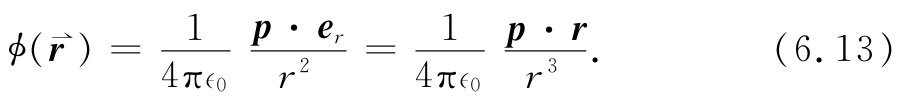
这一公式对于具有任何指向和位置的偶极子都适用，只要r代表从偶极子至所关注之点的矢量。

若想要得到电偶极子的电场，便可通过取ϕ的梯度获得。例如，场的z分量为-∂ϕ/∂z。对于一个沿z轴指向的电偶极子，我们可以应用式（6.9）：

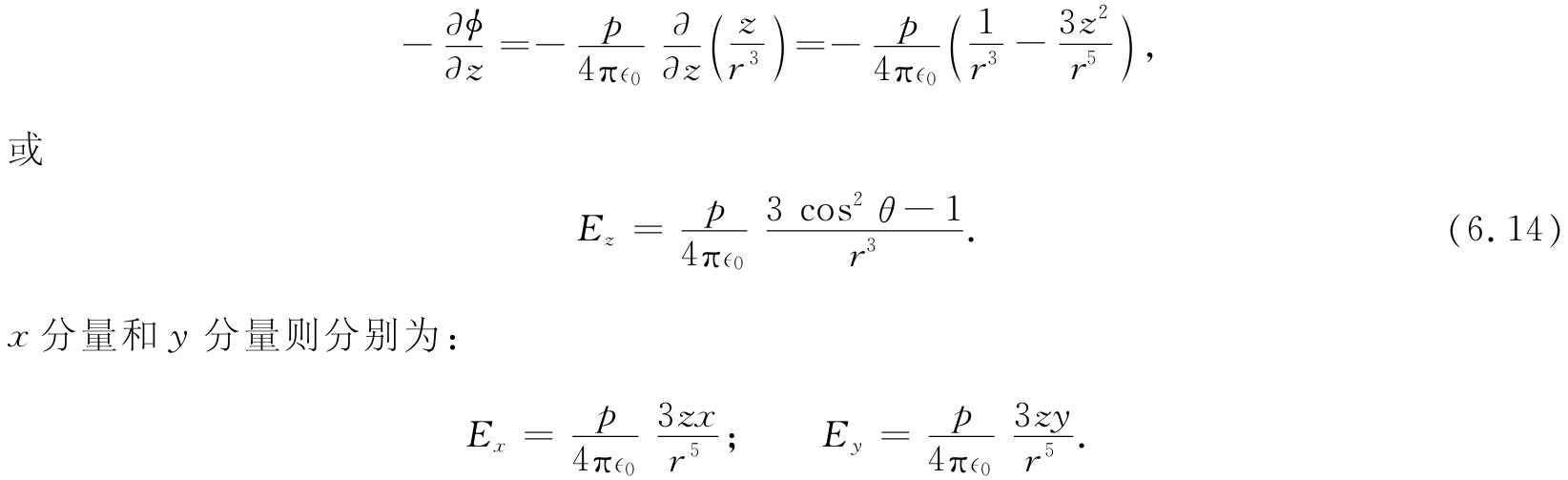
这两个分量还可合成一个垂直 于z轴的分量，我们将称其为横向分量E⊥ ：

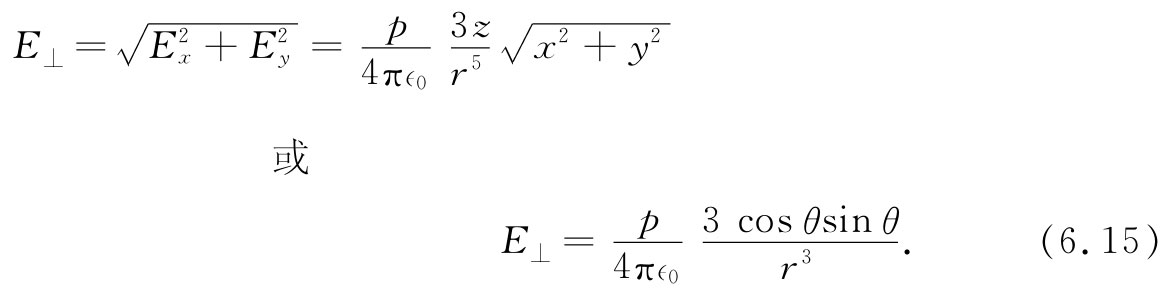
这横向分量E⊥ 处在xy平面内，而且从偶极子轴 直指向外。总场当然是

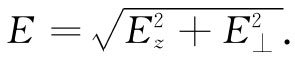
偶极子场与距离的立方成反比。在轴上，即当θ=0时，它比在θ=90°处要强两倍。在这两个特殊角度上电场仅有z分量，但在这两处场的符号却相反（图6-4）.

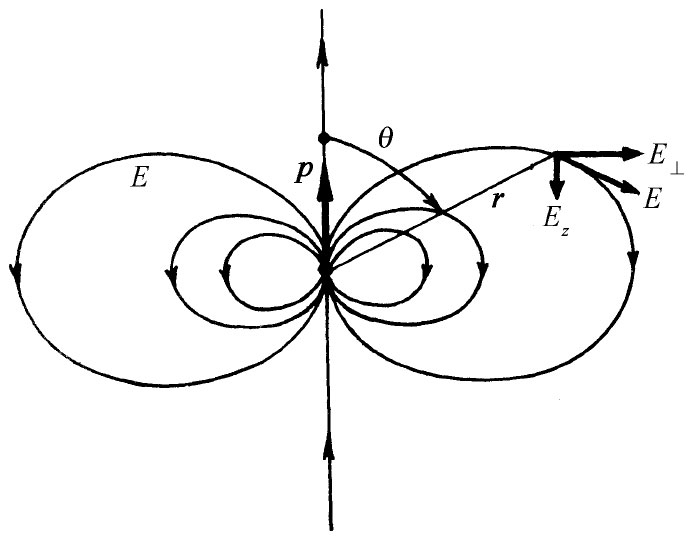
图6-4　偶极子的电场