
关于偶极子公式(6.13),我们愿意指出一件相当愉快的事情。该势也可写成

如果你算出1/r的梯度,你便可以得到
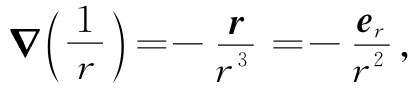
而式(6.16)与(6.13)就彼此相同了。
怎么会想到这一点呢?我们刚好记得,er /r2 曾出现在有关点电荷的场 公式中,而场又是那具有1/r依赖关系的势 的梯度。
之所以能够将偶极子势写成式(6.16)的形式,有其物理 原因。假设有一个位于原点的点电荷q,则在点P(x,y,z)处的势为
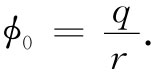
让我们在做这些论证时先丢下1/(4π∈0 ),最后可以把它插进去。现在若把电荷+q向上移动距离Δz,那么在P点的势就将改变一点点,比如说Δϕ+ 。这Δϕ+ 有多大呢?唉呀!这恰好就是——假如让电荷留在原点上不动,而将P向下 移过同样距离Δz——电势将要 改变的数量(图6-5)。也就是说,
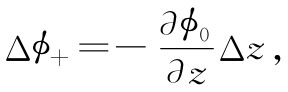
式中Δz指的是与d/2相同的间距。因此,引用ϕ0 =q/r,我们就有该正电荷的势
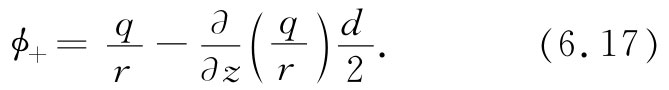
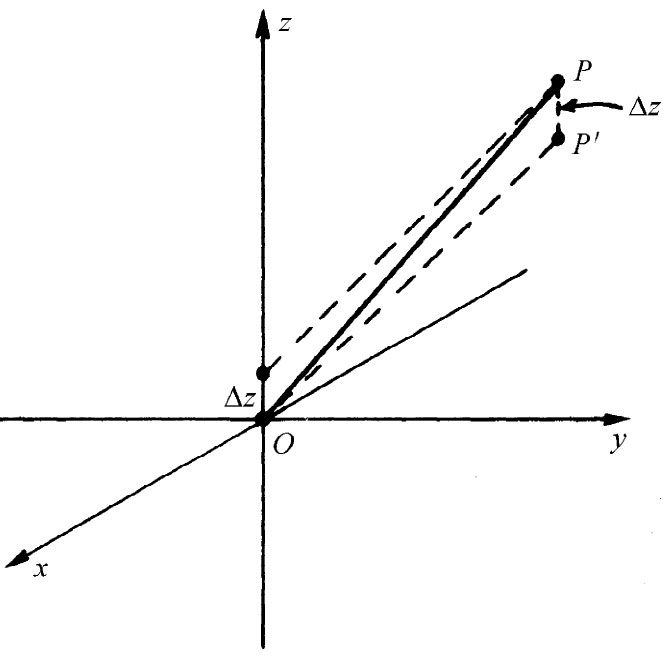
图6-5 来自原点顶上Δz处一个点电荷在P点上的势,等于来自原点处同一电荷在P′点(比P点低下Δz)上的势
对于该负电荷的势,应用同样的道理可写出

总电势等于式(6.17)与(6.18)两者之和:
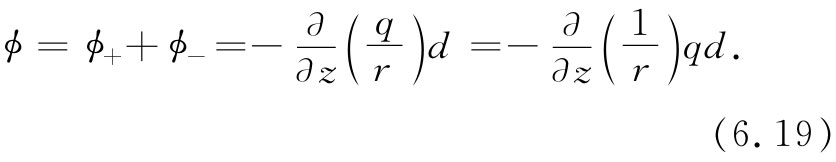
对于其他指向的偶极子,可以将正电荷的位移表示为Δr+ 。然后,我们应该把式(6.17)写成
Δϕ+ =-▽ϕ0 ·Δr+ ,
式中Δr+ 以后被d/2代替。和上面一样,在完成了推导过程之后,式(6.19)就会变成
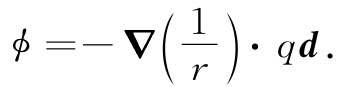
如果我们代入qd=p,并插进1/(4π∈0 ),则上式与式(6.16)正好相同。按另一种方式来看,我们见到偶极子势,即式(6.13),可以解释为
ϕ=-p·▽Φ0 , (6.20)
其中Φ0 =1/(4π∈0 r)仍是一单位 点电荷的势。
尽管对一已知的电荷分布,我们总能够通过积分求得其势,但有时却可能运用一点聪明手法来获得答案,以便节省时间。例如,我们经常可利用叠加原理。如果有这样一个电荷分布,它是由两个电势已知的电荷分布构成的,那么只要将所知的两个势相加起来就能很容易地求得所需的电势。这方面的一个例子是关于式(6.20)的推导,另一个例子如下所述。
假定有一个球面,其表面电荷的分布随极角的余弦而变化。对这么一个分布积分是相当麻烦的。可是令人惊奇,这样的一个分布却可通过叠加原理来加以分析。试设想有一个带着均匀正电荷体 密度的球体,而另一个球体则带有相等的、均匀的负电荷体密度,它们原来就是互相叠合,形成一个中性——也就是不带电——的球体。然后,若该带正电荷球体相对那个带负电荷的球体稍微移动,则不带电的那部分球体仍将保持中性,但有少量正电荷会出现在一边,而少量负电荷则出现在相反的一边,如图6-6所示。若两球的相对位移很小,则净电荷相当于(在球面上的)面电荷,而该面电荷密度将与极角的余弦成正比。
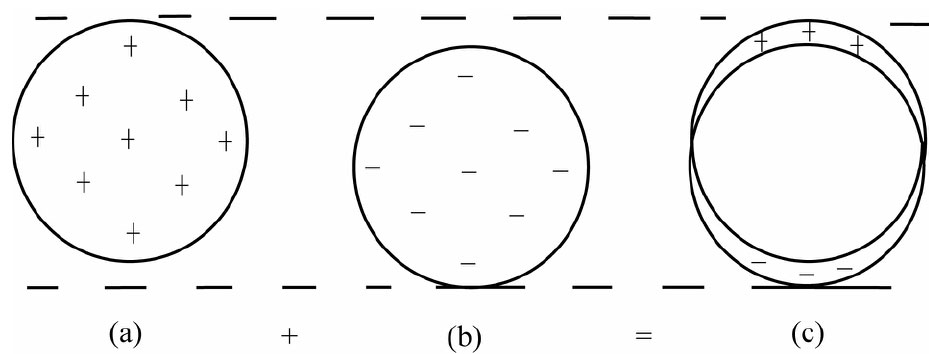
图6-6 彼此间有一微小位移的两个均匀带电球体互相叠加,相当于表面电荷的非均匀分布
现在,如果我们要得到来自这种分布的势,则不必再去做积分。因为我们知道来自每一个荷电球的势——对于在球外的点——与来自一个点电荷之势相同。这两个移动过的球与两个点电荷相似,其势恰好就是一个电偶极子的势。
用这样的方法,你可以证明:在一个半径为a的球面上面电荷密度的分布为
σ=σ0 cosθ,
在球外产生的场恰好就是偶极矩为
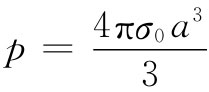
的偶极子产生的场。也能够证明,在该球内的电场是常数,其值为
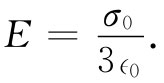
若θ为相对正z轴的角,则在球内的电场在负 z方向。我们刚才考虑的例子并不像它表面看来那么带有人为性,以后将在电介质理论中再次碰到它。