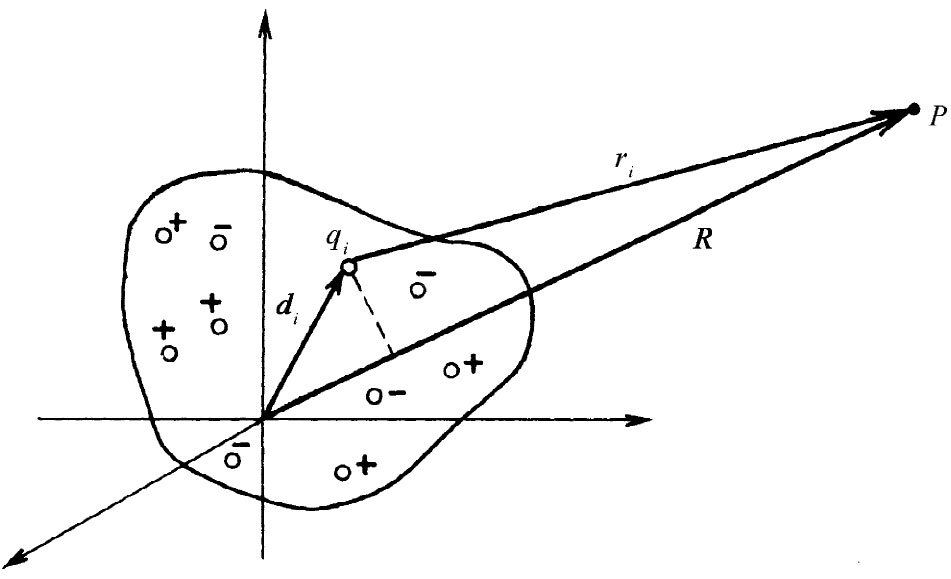
图6-7 一群点电荷在一遥远点P处产生的势的计算
偶极子场还出现在另一个既有趣而又重要的场合中。假设有一个具有复杂电荷分布的物体——像水分子（图6-2）那样——而我们仅仅对远处的场感兴趣。我们将证明，对于距离比物体尺寸要大的情况有可能找到关于场的一个恰当而相对简单的表示式。
图6-7 一群点电荷在一遥远点P处产生的势的计算
我们可将该物体设想成在某一有限区域里的一群点电荷qi ，如图6-7所示（以后若我们愿意，可以用ρdV来代替qi ）. 令每一电荷qi 被置于距原点（选取在该群电荷中间的某处）的位移为di 的地方。在R（R远大于最大的di 值）处的P点，势究竟如何呢？来自整个电荷群的势由下式给出：
式中ri 是从P点至电荷qi 的距离（即矢量R-di 的长度）。现在，如果这些电荷至观察点P的距离巨大，则每个ri 都可以用R来作近似。每一项就都变成qi /R，从而可将1/R取出作为在求和符号前的一个因子。这将向我们提供一个简便的结果
式中，Q恰好就是整个物体的总电荷。这样我们发现：从距离任意一堆电荷足够远的各点上来看，该堆电荷就像一个点电荷似的。这一结果并不太令人惊异。
但若有等量的正电荷和负电荷又该怎么样呢？此时物体的总电荷Q为零。这并不是一种罕见的情况。事实上，正如你们所知道的，物体往往具有电中性。水分子就是电中性的，但其中诸电荷并非完全位于同一点，因而若站得足够近，就应能见到那些分开着的电荷的某些效应。对于来自电中性物体中一个任意电荷分布的势，我们需要一个比式（6.22）更好的近似式。式（6.21）仍然是准确的，不过不能再只是令ri =R，我们需要一个更准确的ri 表达式。如果P点位于遥远距离处，ri 与R的差异可以通过d在R上的投影而得到一个良好近似，正如从图6-7就可以看得出来的那样（你应该设想，实际上P比图上所示的还要遥远得多）。换句话说，若eR 是在R方向上的单位矢量，则我们对于ri 的二级近似为
ri ≈R-di ·eR . （6.23）
我们所真正需要的乃是1/ri ，由于di ≪R，对我们的近似程度来说，1/ri 就可写成
以此代入式（6.21）中，便可得到势
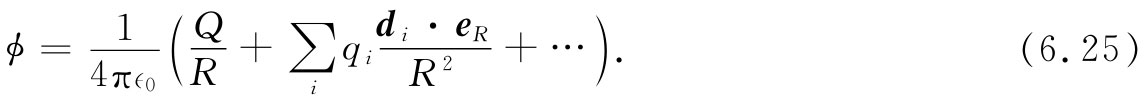
上式中最后三点代表已略去的有关di /R的较高次项。这些项，再加上已获得的那些，就是1/ri 在1/R附近以di /R为幂进行的泰勒展开中的相继的项。
式（6.25）中的第一项，就是在上面获得的，如果物体具有电中性，这一项则取消。第二项依赖于1/R2 ，正如偶极子那种情况。事实上，如果定义
p=∑qi di （6.26）
为该电荷分布的一种特性，那么势式（6.25）的第二项便是
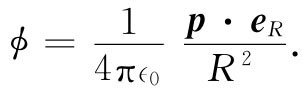（6.27）
这恰好就是一个偶极子势 。p这个量称为该分布的电偶极矩。它是对以前的定义的推广，而在两个点电荷的特殊情况下，它才简化成以前那样。
上述结果是：若距离整体是电中性的任一 团电荷足够远，势就是一偶极子势。它按1/R2 递降，并随cosθ变化——而其强度与该电荷分布的偶极矩有关。正是由于这些缘故，偶极子场才那么重要。因为一对点电荷的那种简单情况是极为罕见的。
例如，水分子就有相当强的偶极矩，由于这偶极矩而产生的电场导致了水的某些重要性质。在许多种分子，诸如CO2 中，由于分子结构的对称性使得其偶极矩为零。因此，对于这些分子我们理应展开得更为准确些，得到势中随1/R3 递降之项，而这称为四极子势。对于这些情况我们将在以后讨论。