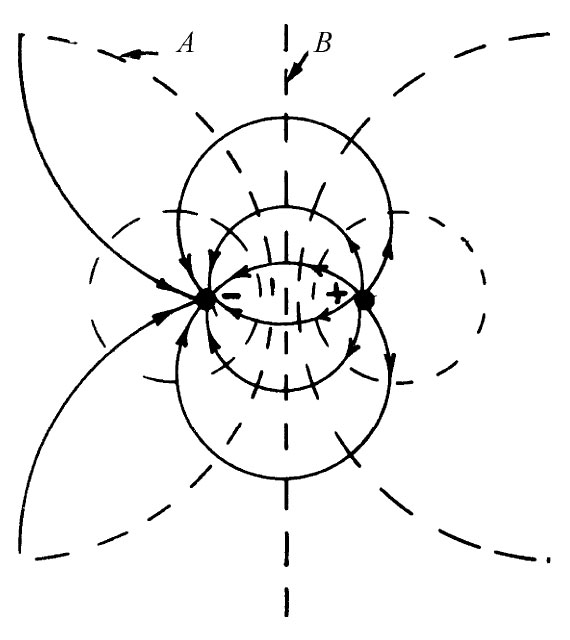
图6-8 两个点电荷的场线和等势面
比方说,我们以前就曾经解出过两个点电荷的场。图6-8表示第4章中通过计算而获得的某些场线和等势面。现在考虑标明为A的那个等势面。假设我们造成一个其形状恰巧与这个面吻合的金属薄片。若把它准确地安放在该面上并调整其势至恰当数值,那就没有谁能够知道它是放在哪里了,因为一切都不会改变。

图6-8 两个点电荷的场线和等势面
可是要注意!实际上我们已经解决了一个新 的问题。我们有这么一种情况:一块具有给定势的弯曲导体面被放在一个点电荷附近。如果被放置在该等势面上的金属片最终能自行闭合(或实际上伸展得足够远),那么就有一种在§5-10中曾考虑过的那样情况,其中空间被分隔成两个区域,其一是在闭合导体壳之内,另一则在其外。我们在那里已经知道这两个区域里的场是互相独立的。因而不管里面怎么样,在导体外面我们应该有相 同的场。我们甚至可以用导电材料来填充整个内部。因此,就已找到了图6-9那种结构的场。在导体外部的空间里,场同图6-8中所示的两个点电荷之场一样。在导体内部,场等于零。并且——正应该如此——刚好在导体外面的电场会与该面正交。
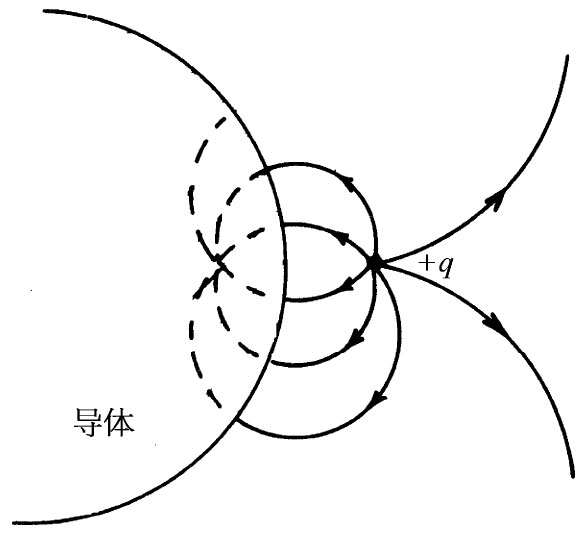
图6-9 在一个形状像图6-8中的等势面A的导体之外的电场
这样,我们便能通过计算q以及在适当位置上一个想象的点电荷-q所产生的场来算出图6-9中的场了。那个我们“想象”其存在于导体表面背后的点电荷称为镜像电荷 。
从书本中你可以找到有关双曲面形状的导体以及其他形状复杂的导体的各种解的长长名单,因而会觉得奇怪,怎么有人竟解决了这些可怕形状的导体问题。原来他们是倒过来求解的!有人解决了给定电荷的一个简单问题。然后,他看到有某一个等势面表现出新的形状,于是就写出一篇论文,指明在这种特定形状的导体外的场可以用某种方法来描述。