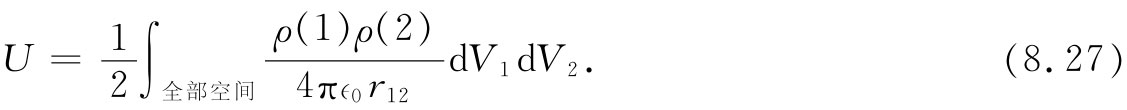
现在来考虑计算静电能的其他方法。这些方法全都可以从基本关系式（8.3）推导出来，该式将每个电荷对的相互作用能对所有电荷对求和。首先，我们希望写出有关电荷分布的能量表达式。按照常规，认为每个体积元dV含有电荷元ρdV。于是式（8.3）将写成
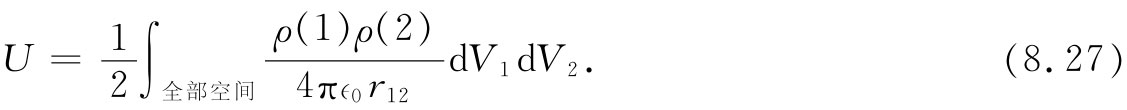
注意：之所以要引入因子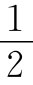
，是因为在对dV1
和dV2
的双重积分中，我们已把所有电荷元对都计算了两遍（没有任何方便的办法可以写出一个能跟踪电荷对，以使每对仅算一次的积分式）。其次，我们也注意到，式（8.27）中对dV2
的积分恰好是点（1）处的势，即是
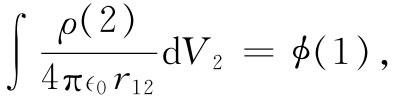
因而，式（8.27）便可以写成
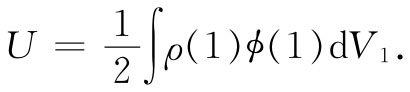
或者，由于点（2）已不再出现了，便可以简单地写成
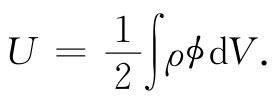（8.28）
这一方程可做如下说明。电荷ρdV的势能等于这电荷与其所在处势的乘积，因此，总能量就是对ϕρdV的积分。但又有因子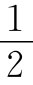
，这仍然是需要的，因为我们把能量计算了两遍。两个电荷间的相互作用能等于其中一个电荷乘以其所在点由另一电荷产生的势。或者
，这也可认为是第二个电荷乘以该点由第一个电荷产生的势。于是对于两个点电荷来说，我们写成
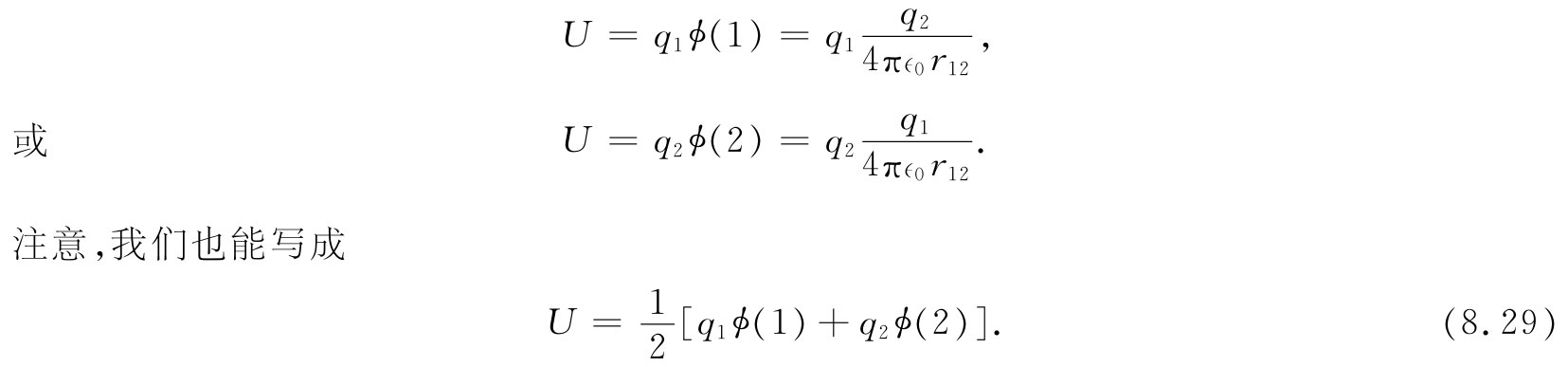
式（8.28）中的积分部分对应于（8.29）中括弧内的两项。这就是为什么我们需要那个因子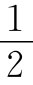
的原因。
一个有趣的问题：这静电能究竟位于何处？或许我们也会问：谁在乎呢？提出这样一个问题有什么意义？如果有一对相互作用着的电荷，则该组合就有某个能量。我们是否有必要说出该能量定位于其中某一电荷处、或另一电荷处、或两个电荷处、或两个电荷之间？这些问题可能不具有任何意义，因为我们实在只知道总能量是守恒的。能量定位在某处 的概念并非必要。
然而，一般说来，假定能说出能量位于某处，确实 具有意义，如同热能那样，那么，我们就应该对能量守恒原理用如下的概念加以推广 ，即如果在一个给定体积内的能量变化了，我们应该能够通过流进或流出该体积的能量来说明这种变化。你认识到，如果某些能量从一处消失而在另一遥远处出现，在其间并没有任何东西正在通过（也就是说，没有任何特殊的现象发生），则我们先前关于能量守恒原理的提法仍然完全正确。因此，目前我们正在讨论关于能量守恒这一概念的推广，也许可以称为局域性 能量守恒原理。这样的一个原理会说：在任何给定体积内能量只能依据流进或流出该体积的量来变化。能量确实有可能是按这一方式局域守恒的。如果事情果然是这样，我们应有一个比起总能量守恒那种简单提法详细得多的定律。实际情况是，在自然界中能量是局域守恒 的。我们能够找到关于能量在哪里以及它如何从一处跑到另一处的公式。
能够说出能量在哪里是重要的事情，还有一个物理 上的原因。按照引力理论，所有质量都是引力之源。我们也知道，根据式E=mc2 ，质量与能量彼此等价。因此，所有能量就都是引力之源。要是我们不能够指明能量的位置，也就不能够指明质量的位置。我们将不可能说出引力场的源究竟位于何处。因而引力理论将是不完整的。
若把我们限制在静电学的范围里，确实无法说出能量的位置在哪里。电动力学完整的麦克斯韦方程会向我们提供多得多的知识（尽管此时答案严格说来仍不是唯一的），因此，我们将在后面一章中再详细讨论这个问题，现在仅仅给出在静电学的特殊情况下的那种结果。能量在电场所在的空间里，这似乎很合理，因为我们知道，当电荷加速时它们会辐射出电场来。我们愿意这么说，即当光或无线电波从一点传播至另一点时，它们随身带着能量，但是在这些波中却没有电荷。因此喜欢把能量定域在电磁场所在的地方，而不是在其发出来的电荷那里。于是我们不用电荷而是用由电荷所产生的场来描述能量。事实上，能够证明式（8.28）在数值上 等于
于是，可把此式解释为：当电场存在时，在该空间里就定域了能量，其密度 （单位体积能量）为：
这一概念如图8-8所示。
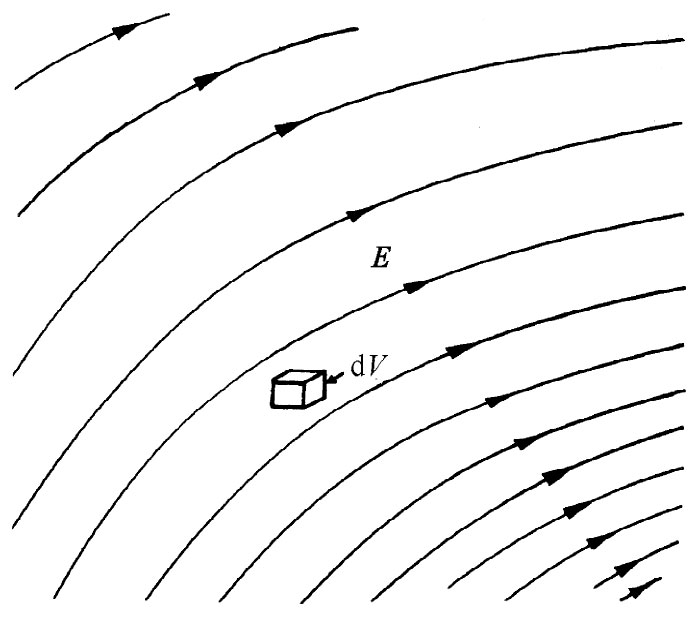
图8-8 在电场中每一体积元dV=dxdydz含有能量（∈0 /2）E2 dV
为要证明式（8.30）与静电学定律一致，我们现在把曾在第6章中得到的有关ρ与ϕ的关系
ρ=-∈0 ▽2 ϕ
引入（8.28）式，因而得到
写出被积函数的各个分量后，可见到
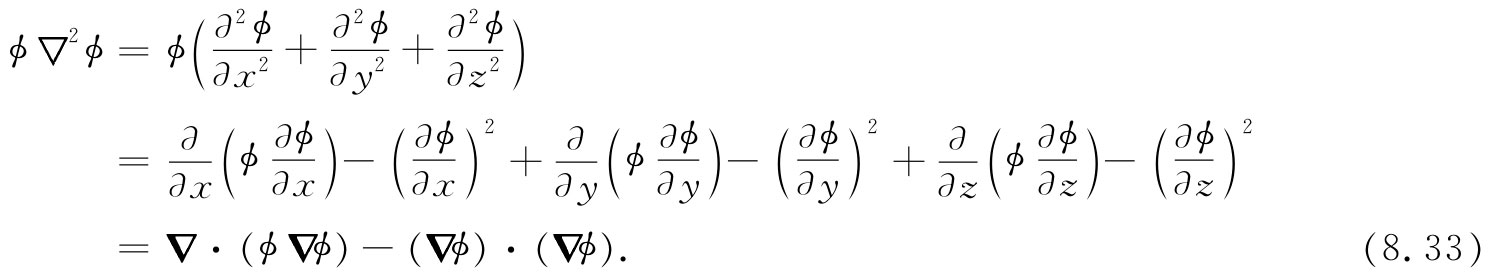
于是我们的能量积分为
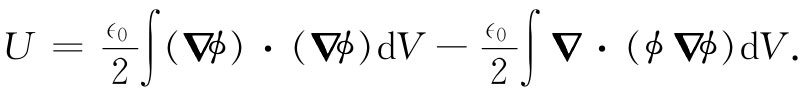
可以利用高斯定理把第二个积分变成一个面积分：
∫体积 ▽·（ϕ▽ϕ）dV=∫曲面 ϕ▽ϕ·nda. （8.34）
我们要在所有电荷都被放置在某个有限距离内的假定下，对面积伸展至无限远处（从而使体积分变成对全部空间的积分）的情况计算该面积分，进行积分的简单办法乃是取一个具有巨大半径而其中心位于坐标系原点的球面。我们知道，当离所有电荷都很远时，ϕ会随1/R变化，而▽ϕ则按1/R2 变化（如果那里分布中的净电荷为零，则这两项均将随R下降得更快）。由于该巨大球面的面积随R2 增大，当球面的半径增大时，那面积分将按照（1/R）（1/R2 ）R2 =（1/R）而下降。因此，如果把全部空间都包括在我们的积分之内（R→∞），则该面积分将趋于零，而结果为：
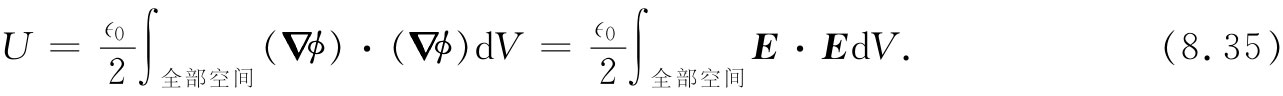
由此可见，对于任何电荷分布，我们总能将其能量表达为对场中能量密度的积分。