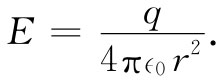
我们的新关系式(8.35)说明,即使单个点电荷q也将有若干静电能量。在这种情况下,电场是由下式给出的:
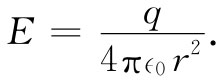
因此,在距离电荷r处的能量密度为
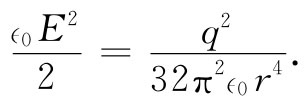
我们可以取一个厚度为dr、面积为4πr2 的球壳作为体积元。总能量为
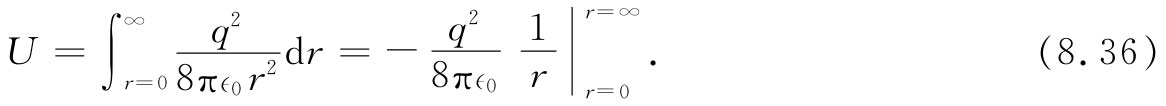
现在对于在r=∞的上限毫无困难。但对于一个点电荷来说,我们本应从下限r=0积起,而这会给出一个无限大的数值。式(8.35)讲:在一个点电荷的场中会有无限大的能量,尽管我们过去是从只在点电荷之间 才有能量那种观点出发的。在我们原来关于一群点电荷的能量公式(8.3)中,并未把电荷对于其本身的任何相互作用能包括在内。实际发生的情况乃是:当我们转变到电荷的连续分布、即式(8.27)时,就曾计入了每一无限小 电荷与所有其他无限小电荷之间的相互作用能。同一计算也包括在式(8.35)之内,因而当将其应用于有限多 点电荷时,我们已把从无限小部分电荷聚集起来所要的那种能量也包括进去了。事实上,我们将注意到:若应用有关一个带电球体的能量表示式(8.11),并让其中半径趋于零,则我们也会获得式(8.36)中的那种结果。
必须断言,把能量定域在场中的那种概念同存在点电荷的假设是彼此不相容的。一种摆脱困难的办法应该说明,像电子那样的基本电荷并不是一些点,而实际上是电荷的微小分布。或者,本来我们也可以这样讲:在十分微小的距离内,电学理论已有些错误,或局域能量守恒的概念有点不对头。对于这两种观点中的任一个观点都存在困难,这些困难从未得到克服,一直遗留到今天。此后在某个时候,当我们已讨论过诸如电磁场中的动量那样一些附加概念之后,就将对在理解大自然时所碰到的这些基本困难给予更全面的估量。