我们将首先讨论非极性分子的极化。可以从最简单的单原子气体（例如氦）开始。当这样一种气体的原子处在电场中时，电子会被场拉向一边而核则被拉向另一边，如图10-4所示。虽然相对于我们在实验上所能施加的电力来说原子是十分坚硬的，但是电荷中心仍存在微小的净位移，从而感生了一个偶极矩。对于弱场来说，这位移量、也就是偶极矩，与电场成正比。产生这种感生偶极矩的电子分布的位移称为电子的极化 。
过去与折射率理论打交道时，我们曾在第1卷第31章中讨论过电场对原子的影响。如果你稍微思考一下便将看到，现在我们应该做的和那时做过的完全相同。但现在需要操心的只是不随时间变化的场，而折射率却与随时间变化的场有关。
在第1卷第31章中我们曾经假定，当原子被置于振动的电场中时，原子内电子的电荷中心会遵循下列方程而运动：
式中，第一项为电子质量乘以其加速度，第二项为恢复力，而右边那一项则代表来自外电场的力。若电场以频率ω变化，则方程式（11.2）的解为
（11.3）
这表明，当ω=ω0 时，会发生共振。当以前得到这个解时，我们曾把它理解为该式表明ω0 是光（到底是在可见光区还是在紫外光区，则取决于该原子）被吸收的频率。然而，现在我们感兴趣的却只是恒定场的情况，也就是，只对于ω=0的场有兴趣，因而可以将式（11.2）中的加速度项略去，并得出电荷的位移为
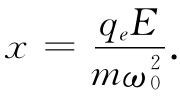（11.4）
由此可见，单个原子的偶极矩为
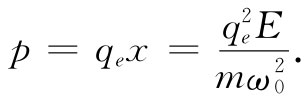（11.5）
在上述这种理论中，偶极矩p确与电场成正比。
人们经常把上式写成：
p=α∈0 E （11.6）
（∈0 又一次由于历史原因而被放了进去）。其中常数α称为原子的极化率，并具有L3 的量纲。它是由电场在原子中感生一个偶极矩的难易程度的一种量度。将式（11.5）和（11.6）两者比较，我们这一简单的理论讲
设单位体积中共有N个原子，则单位体积的极化强度P就是
P=Np=Nα∈0 E. （11.8）
把式（11.1）和（11.8）两者合拼在一起，我们得到
或者，利用式（11.7），可得
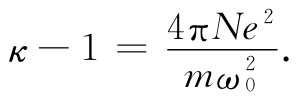（11.10）
从式（11.10）我们会预料到不同气体的介电常量κ可能与该气体的密度及其对光的吸收频率有关。
当然，上述公式只是一种近似，因为在式（11.2）中我们所选择的模型略去了量子力学的复杂性。例如，我们曾经假定每个原子仅有一个共振频率，而实际上却有许多个。为了正确地计算原子的极化率α，我们必须应用完整的量子力学理论，但上面的经典概念却已为我们提供了一个合理的估计。
让我们来看看，对某种物质的介电常量我们是否能得到一个正确的数量级。假定我们对氢做尝试，过去（在第1卷第38章中）就曾估计过电离一个氢原子所需的能量约为
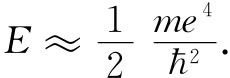（11.11）
为了对那个固有频率ω0 做出估计，可以令这一能量等于ћω0 ——即固有频率为ω0 的原子振子的能量。这样我们就得到：
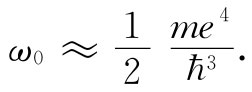
若现在把ω0 的这个值应用于式（11.7），则可求得电子极化率为：
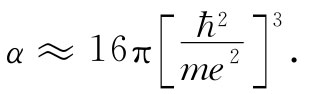（11.12）
［ћ2 /（me2 ）］这个量是玻尔原子的基态轨道半径（见第1卷第38章），等于0.528Å。因处于标准压强和标准温度（1atm、0℃）下的气体每立方厘米都具有2.69×1019 个原子，所以式（11.9）就给出：
κ=1+（2.69×1019 ）16π（0.528×10-8 ）3 =1.00020. （11.13）
氢气的介电常量已测定为
κ实验 =1.00026.
由此可见，我们的理论已差不多正确了。不应该期望任何比此更佳的结果，因为测量当然是用正常氢气进行的，所以它所含的是双原子分子，而不是单原子分子。如果分子中各原子的极化与彼此分开的原子的极化不完全相同，那应不足为怪。可是，实际上分子效应却不是那么大。对于氢原子的α进行严格的量子力学计算给出比式（11.12）约大12%的结果（即将16π改变成18π），因而预言一个更接近于观察值的介电常量。不管怎样，我们上述的电介质模型显然已相当之好。
对上述理论的另一个考验，是将式（11.12）试用于具有更高激发频率的那些原子。例如，需要有24.6eV才能将氦原子中的电子拉出来，这可与电离氢所需的13.6eV做比较。因此，我们会期待，氦的吸收频率ω0 应比氢约大一倍，从而它的α可能为氢的四分之一大。期待值为
κ氦 ≈1.000050.
实验值为
κ氦 =1.000068.
所以你们可以看到，我们的粗糙估计方向是对头的。至此，我们已了解非极性气体的介电常量，然而那不过是定性的，因为我们还未用到有关原子中电子运动的那种正确的原子理论。