现在要转到一个有趣而又复杂的问题——致密材料中的介电常量问题。假设我们选取液态氦或液态氩,或其他某种非极性材料,我们仍将期待会有电子极化。可是在致密材料中,P可以很大,从而使作用在各个别原子上的场会被其近邻原子的极化所影响。问题在于,作用于各个别原子上的电场究竟如何?
设想有一液体被置于一电容器的两极之间。若板上带电,则这些电荷将在液体里产生一个电场。但在各个别原子中也有电荷,因而总场E便是这两种效应之和。这一真正电场在液体里从一点至另一点变化得十分迅速。这电场在原子里面很强——特别是刚好在核附近——而在原子与原子之间就相对弱了。两板间的电势差是对这一总场的线积分。若略去一切微小尺度上的变化,则可以认为存在一个平均 电场E,它恰好就是V/d(这是上一章中我们所曾采用过的场)。应该把这个场想象成在一个含有许多个原子的空间内的平均场。
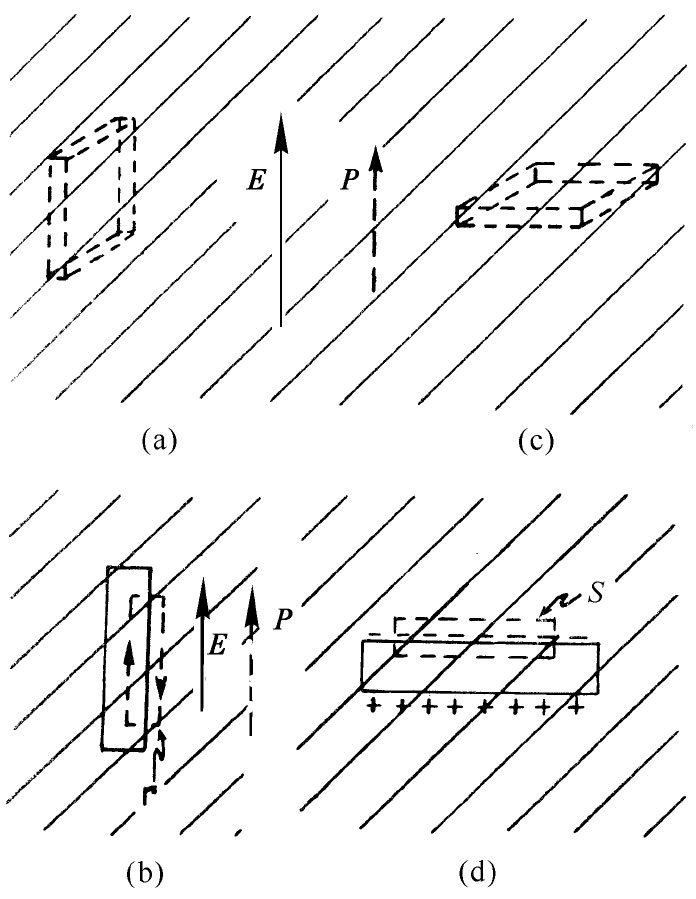
现在你也许认为,一个处在“平均”位置上的“平均”原子会感觉到这一个平均场。可是事情却并不那么简单,若想象电介质中有不同形状的空腔,则通过考虑里面所发生的情况就可证明这点。例如,假设在一块被极化了的电介质里挖出一个槽来,该槽的取向与电场平行,如图11-5(a)所示。由于我们知道▽×E=0,故在环绕图(b)所示曲线Γ所取的线积分就应等于零。槽中的场所提供的贡献必定恰好抵消来自槽外的场的贡献。因此,实际上在一条狭长槽的中心处得到的场E0 等于在电介质里找到的平均电场E。

图11-5 从电介质里切割出一个槽来,槽中的场取决于该槽的形状及取向
现在考虑大的侧面与E垂直的另一种槽,如图11-5(c)所示。在这种情况下,槽里的场E0 就不同于E,因为极化电荷出现在槽面上了。如果我们应用高斯定律于图(d)中所画出来的那个S面,则发现槽里 的场E0 由下式给出:

式中E仍然是电介质中的场(该高斯面中含有面极化电荷σ极化 =P)。我们曾在第10章中提及,∈0 E+P这个量常称为D,因而∈0 E0 =D0 就等于在电介质里的D。
在物理学较早期的历史中,当时人们认为每个量都要直接由实验来下定义是非常之重要的,因而当发现不必在原子之间到处爬行就能够给电介质里的E和D下定义时,感到十分喜悦。平均场E在数值上就等于平行于场的槽中所量得的场E0 。通过挖一个垂直于场的槽,并求得其中的E0 ,从而可测得场D。但从来没有人按照这种办法把它们测量出来,因而那不过是一种哲学上的东西而已。
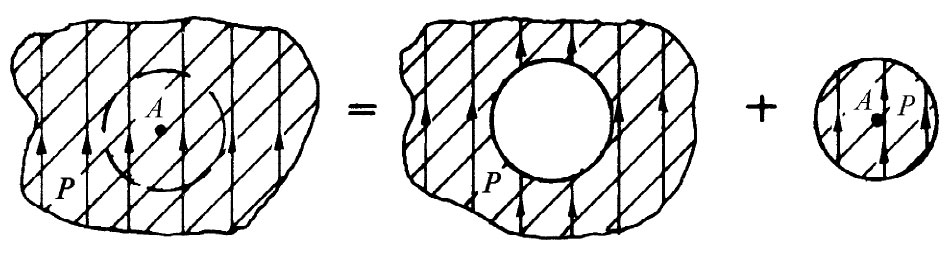
图11-6 介质内任一点A的场,可认为是一个球形空腔里的场与一个球形塞子所产生的场之和
对于结构不太复杂的大多数液体来说,我们可以期待:平均地说一个原子发现自己受到其他原子的包围,作为很好的近似,认为它处在一个球形的空腔 之中。因此,我们就会问:“在一个球形空腔中的场到底怎样?”注意!若在一块均匀极化材料中,设想挖出一个球形空腔,那不过是把极化材料中的一个球体移出去罢了,这样就可将腔里之场找出来(我们必须想象,在挖出该空腔之前极化已被“冻结”了)。然而,根据迭加原理,在该球体移出之前,电介质内部的场等于球体体积外所有电荷的场再加上极化球内部电荷之场。这就是说,若我们把在均匀电介质里的场叫作E,则可以写成
E=E空腔 +E塞子 . (11.23)
式中,E空腔 指在该腔里之场,而E塞子 则为一个均匀极化球内部的场(见图11-6)。由一个均匀极化球所产生的场,如图11-7所示。在这个球体之内,场是均匀的,其值为

应用式(11.23),我们得到
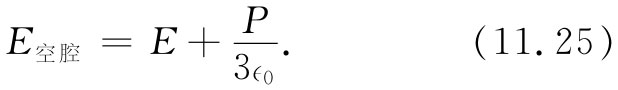
在一个球形空腔里的场比平均场要大P/3∈0 (系数1/3表明,球形空腔里的场介于平行于场的槽内的场和垂直于场的槽内的场之间)。
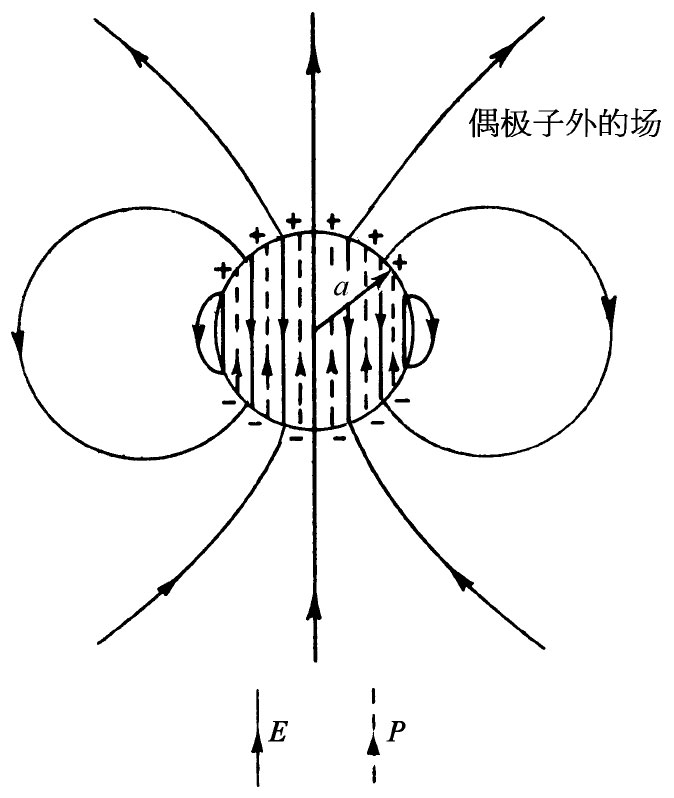
图11-7 一个均匀极化球体的电场