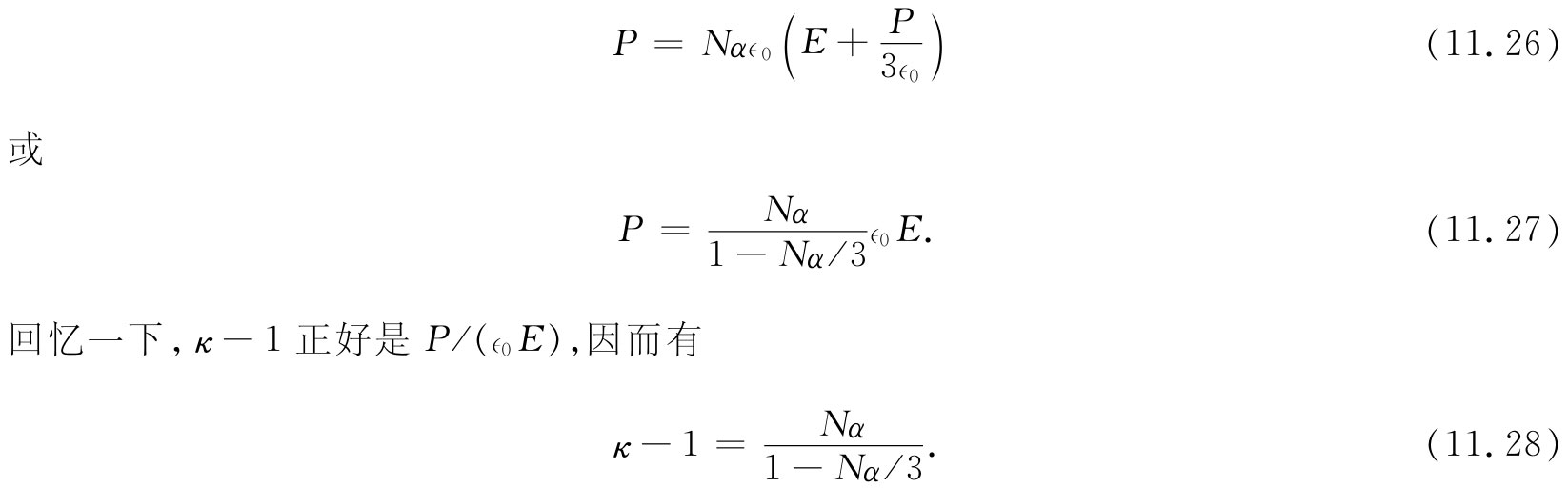
在液体中,我们期待对各个别原子起极化作用的场类似E空腔 ,而不是E。如果把式(11.25)的E空腔 用作式(11.6)中的极化场,则式(11.8)变成
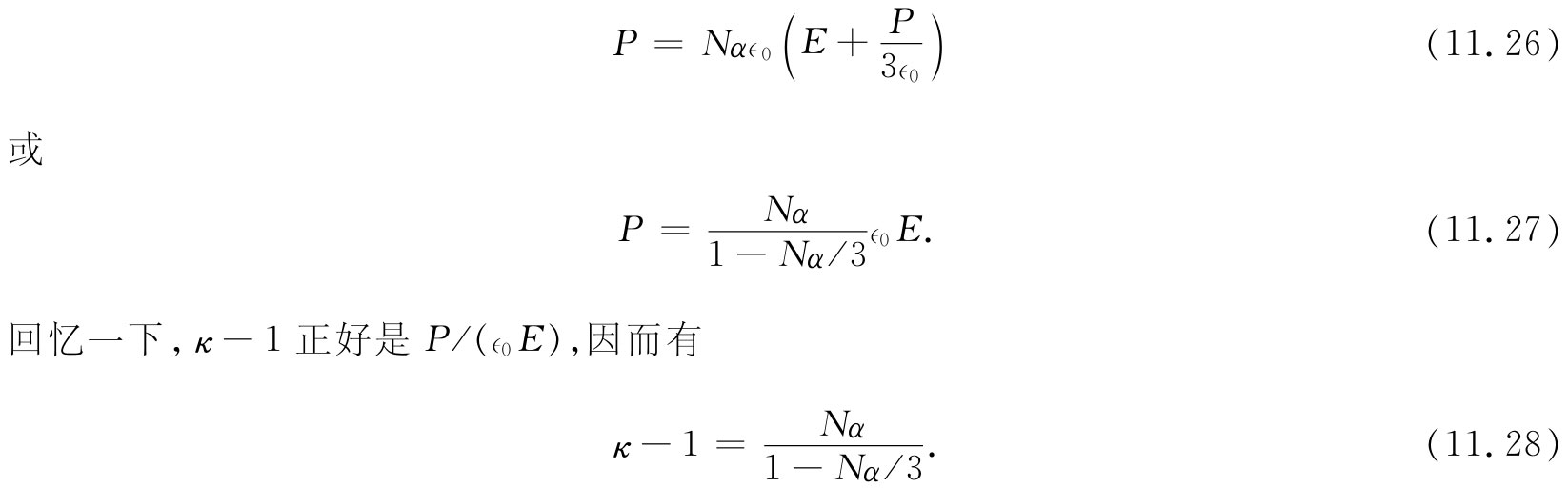
这为我们提供了用原子极化率α表达的液体介电常量。式(11.28)称为克劳修斯-莫索提 方程。
每当Nα非常小时,如在气体那种情况(因为密度N很小),于是项Nα/3与1相比可以忽略,因而我们得到以往那个结果,即式(11.9),
κ-1=Nα. (11.29)
让我们拿式(11.28)同某些实验结果进行比较。有必要首先考虑能用κ的测量值通过式(11.29)算出α来的那些气体。例如,对于在0℃的CS2 来说,介电常量为1.0029,所以Nα就是0.0029。气体的密度一般容易算出,而液体的密度则可从手册中找到。液态CS2 在20℃的密度比在0℃时该气体的密度要高381倍,这意味着它处在液体时的N比处在气体时高381倍。因而——倘若我们近似地认为CS2 凝结成液体时,其基本原子极化率并不发生变化——在液体中的Nα便是0.0029的381倍,即1.11。注意项Nα/3的值接近0.4,所以就显得极为重要。用这些数字我们预测介电常量等于2.76,与2.64的观测值符合得相当好。
在表11-1中,我们列出了几种不同材料的一些实验数据(从《化学与物理学手册 》中得来的),以及按刚才所述的方法由式(11.28)计算出来的介电常量。对于Ar和O2 ,观测值与理论值的符合程度甚至比CS2 还要好——而对于CCl4 理论值与观测值的符合程度就不那么好了。大体上,所得结果都表明式(11.28)用起来十分良好。
表11-1 由气体的介电常数算出液体的介电常量
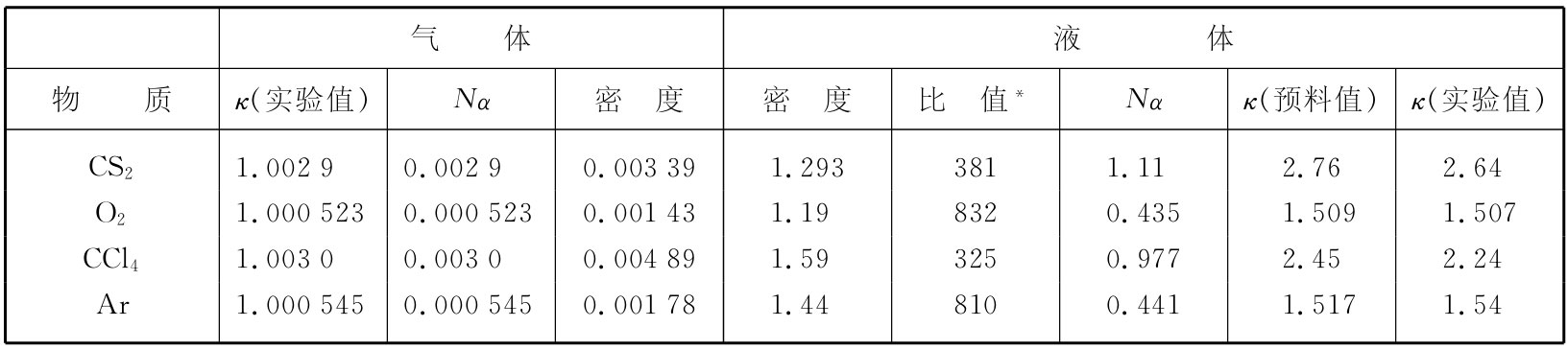
* 比值=液体密度/气体密度。
我们关于式(11.28)的推导仅适用于液体中的电子 极化。对于H2 O那样的极性分子来说,这个式子就不正确了。如果对水也做同样的计算,便会得出Nα等于13.2,那意味着在该液体的介电常量为负值 ,但κ的观测值却是80。这一问题牵涉到得对永久偶极矩作正确的处理,而昂萨格(Onsager)就曾指出过正确的方向。现在我们没有时间来讨论这种情况,但若你有兴趣的话,可参考克脱耳(Kittel)所著的《固体物理导论 》,书中对这个问题有所论述。