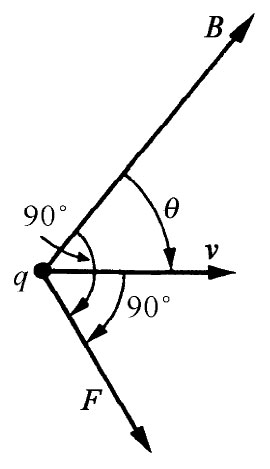
作用于一电荷上的力不仅取决于它的位置,而且还取决于它运动的速度。空间每一点可由两个能确定作用于电荷上的力的矢量来做标志。首先,电力 提供了与电荷运动无关的一部分力,我们用电场E来描述它;其次,另一部分力,称为磁力 ,那是有赖于电荷的速度的。磁力还具有一种奇怪的方向特性:在空间任一特定点上,这力的方向 和大小 均取决于该粒子的运动方向。在任一时刻,这力总是垂直于速度矢量;并在任一特定点上,这力又总是与空间中某一固定方向 成直角(见图13-1);而且,力的大小是与垂直于这一规定方向的速度分量 成正比的。所有这一切行为都能由一个定义为磁场矢量的B来加以描述。这个矢量不仅在空间规定出唯一方向,并且还规定力与速度成正比的那个比例常数,从而写出磁力为qv×B。于是,作用于电荷上的总电磁力就可以写成
F=q(E+v×B). (13.1)
这称为洛伦兹力 。

图13-1 作用于一运动电荷上与速度有关的那一部分力,与v及B的方向都成直角。它也与垂直于B的v的分量(即vsinθ)成正比
磁力可用一根磁棒靠近一阴极射线管而轻易地加以演示。电子束的偏转,表明磁铁的存在产生了一个作用于电子而与其运动方向成直角的力,如同在第1卷第12章中我们曾描述过的那样。
磁场B的单位显然是1NsC-1 m-1 。这同一单位也是1Vsm-2 。它也称为1Wbm-2 。