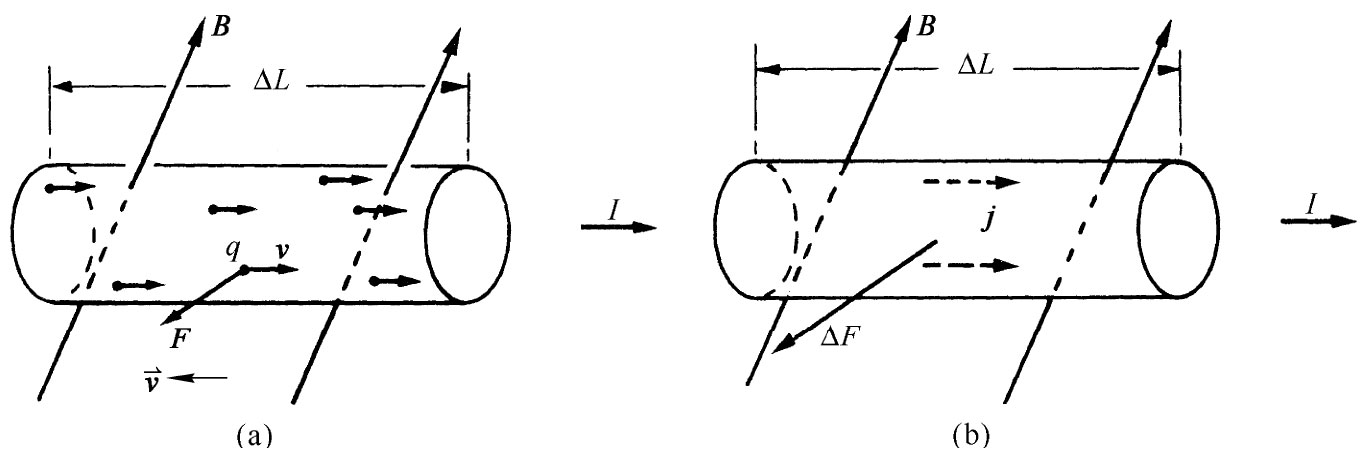
现在我们准备求磁场作用于一载流导线上的力。电流由以速度v沿导线运动的带电粒子组成。每一个电荷都感受到一个横向力
F=qv×B
[图13-5(a)]。如果单位体积含有N个这样的电荷,则在导线的一个小体积ΔV内的数目为NΔV。作用于ΔV上的总磁力ΔF等于作用在各电荷上之力的总和,即是,
ΔF=(NΔV)(qv×B).
但Nqv恰好就是j,因而
ΔF=j×BΔV (13.9)
[图13-5(b)]。作用于单位体积的力为j×B。

图13-5 作用于一载流导线上的磁力等于对各个运动电荷作用力的总和
如果在一根截面为A的导线中,流经导线的电流是均匀的,则可取截面为A而长度为ΔL的一段柱体作为体积元。于是
ΔF=j×BAΔL. (13.10)
现在就可以把jA叫作导线中的电流矢量I(它的大小为导线中的电流,而其方向则是沿着导线)。这样,
ΔF=I×BΔL. (13.11)
因此作用于单位长度导线上的力为I×B。
上式显示了一个重要结果,即由于导线内电荷运动而作用于导线上的磁力,仅取决于总电流,而与其中每一粒子所带的电荷量——甚至连符号!——都无关。作用于磁铁附近导线上的力,通过观察接通电流时线的偏转不难加以演示,正如在第1章中所曾描述过的那样(见图1-6)。