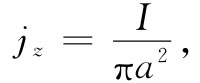§14-3　直导线

作为第一个例子，我们将再次求一直导线的场——这在上一章中已经应用式（14.2）和一些关于对称性的论据而解出。我们考虑半径为a而通有恒定电流I的一根长直导线。与静电学中电荷分布于一导体上的情况不同，导线中的恒定电流乃均匀地分布在该线的横截面内。如果选取如图14-3所示的坐标系，则电流密度矢量j便只有一个z分量，其大小在导线内为

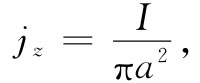　（14.20）

而在导线外则为零。

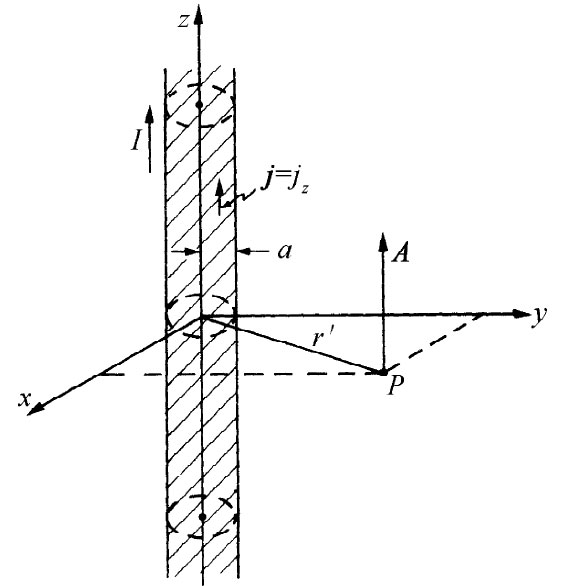
图14-3　沿着z轴而通有均匀电流密度j的一根长圆柱形导线

既然jx 和jy 都是零，我们便立即有

Ax =0；　Ay =0.

为求得Az ，我们可以利用带有均匀电荷密度ρ=jz /c2 的导线，解出其电势ϕ。在一无限长均匀带电圆柱体之外的各点，其电势为

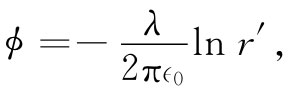
式中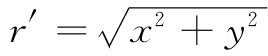 ，而λ则为单位长度的电荷，即πa2 ρ。所以对于通有均匀电流的长直导线之外的某点，Az 应该为

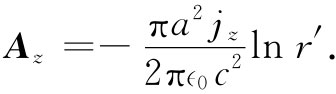
由于πa2 jz =I，上式还可以写成

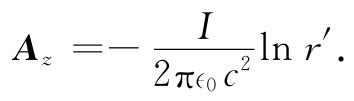　（14.21）

现在就可由式（14.4）求出B。由于该式的六个微商中只有两个不等于零，因而得出

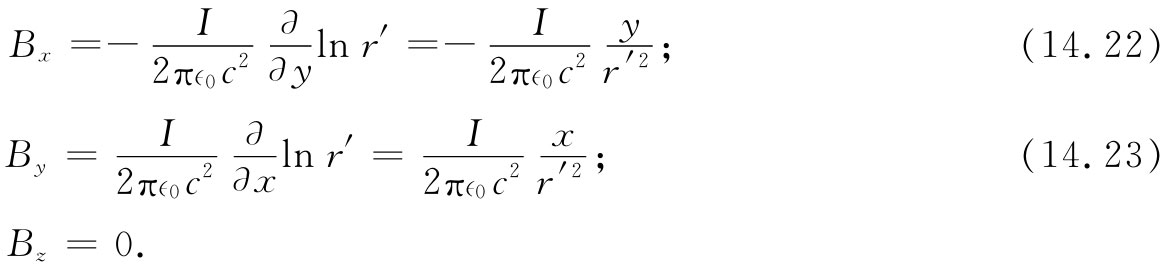
我们得到了与以前相同的结果：B环绕着导线，其大小为

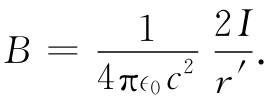　（14.24）