
在本节中我们很想讨论下述问题:矢势是否只是一种用作计算的工具——如同在静电学中所用的标势那样——或者矢势是一个“真实”的场?难道磁场,由于造成了作用于一个运动粒子上的力,它就是一个“真实”的场吗?首先,我们应该说“一个真实的场”这一短语并不非常有意义。其一,无论如何你可能不会感觉到磁场十分“真实”,因为甚至整个有关场的概念都相当抽象。你不能伸出手来感受磁场。而且,磁场之值并不十分确定,例如,通过选用一适当的运动坐标系,你可以使在某一给定地点的磁场消失。
我们这里所谓“真实”的场是:一个真实的场就是被用来避免超距作用概念的一个数学函数。如果有一个带电粒子位于位置P,它会受到放在离P点某个距离处的其他电荷的影响。描述这相互作用的一种方法是讲其他电荷会在P点周围形成某种“状况”——不管它可能是什么状况。倘若知道了该状况,并通过给出电场和磁场来加以描述,则我们便能完全确定该粒子的行为——不需进一步询问那些情况是怎样产生的。
换句话说,若其他电荷以某种方式发生了改变,但由P点的电场和磁场所描述的P点的状况却依然未变,则该电荷的运动也将保持一样。这么一来,一个真实的场就是我们用某种方法规定的一组数字,即在某点 所发生的无论什么事情都仅取决于该点 的这些数字。我们不必知道其他地方将发生的更多事情。正是在这一种意义上我们将要来讨论矢势是否是一种“真实”的场。
你可能对这个事实感到奇怪,即矢势并不是单值的,它可以通过加上任一标量的梯度而改变,但丝毫不会改变施于粒子上的力。然而,这却与我们现在所谈的这种意义上的真实性问题毫不相干。比如,在某种意义上磁场可以通过相对论性变换而改变(E和A场也都如此),但我们却不会去操心如果场可以 这样改变而发生的事情。这实际上并不会造成任何差别,与矢势是否是一种用来描述磁场的适当的“真实”场或只是一个有用的数学工具的问题毫无关系。
关于矢势A的用处我们也应作出一些评论。我们已见到,利用它并通过正常步骤即可以计算已知电流的磁场,正如可用ϕ来求电场。在静电学中我们曾看到,ϕ是由一个标量积分给出的:

通过三次微分运算,便可从这个ϕ获得E的三个分量。这个步骤通常要比在下列矢量式中算出三个积分较易于掌握:

首先这里就有三个积分,其次,每个积分一般又较困难。
对静磁学来说,优点远没有那么明显。A的积分就已经是一个矢量积分:

这当然包含了三个积分。并且,当我们取A的旋度以获得B时,不得不做六次微商把它们一对一对地结合起来。在大多数问题中,这一步骤是否确实比直接从下式算出B来较为容易,就不是立即能看清楚的:
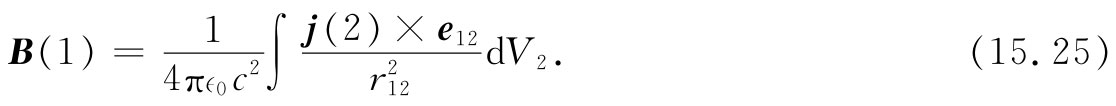
对于简单问题,应用矢势往往较为困难,那是由于下述原因。假设我们只对一点的磁场B感兴趣,而问题又具有某种好的对称性——比如说,我们要求出在一环形电流的中轴上某一点的场。由于对称性,我们可以通过对式(15.25)的积分而很容易地获得B。然而,假如我们先求出A,则还得从A的微商 算出B,因而就一定要知道在所注意点邻近 所有点的A值。而这种点大多数位于对称轴的外面,从而使A的积分变得较复杂。例如,在那圆环问题中,我们不得不用到椭圆积分。在这样的问题中,A显然不是十分有用。但对于许多复杂问题,用A来计算比较容易,那却是真的。不过为了证明技术上的这点方便就认为使你多学习一种矢量场是正当的,那就有点困难了。
我们引进了A是因为它的确 具有重要的物理意义。它不仅与电流的能量有关,如在上节中我们曾经见到的;而且它还是在上述意义上的一种“真实”的物理场。在经典力学中我们显然可把作用于一粒子上的力写成下式:
F=q(E+v×B). (15.26)
因而若给出了力,则关于运动的一切事情就都确定了。在任何B=0的区域中即使A不为零,诸如在一螺线管外面,那里并没有可觉察到的A的效应。因此人们早已相信A不是一个“真实”的场。然而事实却证明,存在着涉及到量子力学的现象,它们表明场A实际上就是我们定义过的那种意义的“真实”的场。在下一节中我们将向你们说明那是怎么回事。