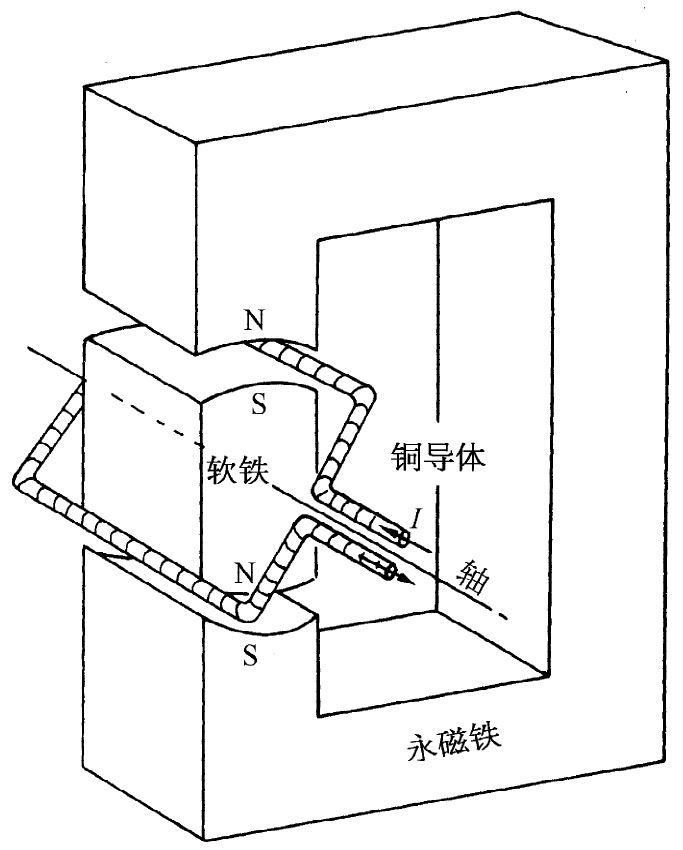
图16-1 一部简单电磁式发动机的示意轮廓图
1820年对电和磁间密切关系的发现曾令人十分兴奋——在那以前,电和磁这两个课题一直被认为是完全互相独立的。首先发现的是导线中的电流会产生磁场,接着于同一年中,又发现载流导线在磁场中会受到力的作用。
每当机械力存在时,令人兴奋的一件事是,利用它在机器中做功的可能性。当上述现象被发现后,几乎立即就有人开始利用这些作用于载流导线上的力来设计电动机了。这种电磁式发动机的原理如图16-1中裸露轮廓图所示。用一块永磁铁——通常配合一些软铁片——在上下两槽里产生磁场。在每一个槽的对面都有南北两极,如图所示。在每个槽中放置铜制矩形线圈的一边。当电流通过线圈时,在两槽处的电流互相反向,因而力也反向,这样便产生一个环绕轴线的力矩。如果线圈安装在传动轴上以便转动,则可与滑轮或齿轮互相配合而做功了。

图16-1 一部简单电磁式发动机的示意轮廓图
同样的设想也可用来制作电学测量方面的灵敏仪器。自从该力的规律被发现之后,电学测量的精确度就大大提高了。首先,可以使电流绕行许多匝而不仅仅是一匝,以促使这种电动机的力矩大大增加。于是,这个线圈又可以装配得用一个很小的力矩便能够转动——或者把它的转轴装在一个十分精致的宝石轴承上,或者用十分细小的金属丝或石英丝来悬挂该线圈。于是一个极小电流便能使线圈转动,而对于小角度来说这转动的大小将与电流成正比。把一指针粘紧在该线圈上,或对于非常精密的仪器,则通过安装在线圈上的一个小镜子来观察标尺的像的移动,这转动的大小就可以测到了。这样的仪器叫作电流计。至于伏特计和安培计,也是基于相同的原理工作的。
这一概念也可用来大规模地制造提供机械动力的大型电动机。利用安装在轴心上的一组触点可使线圈每转半周接法就变换一次,这样,线圈便能不断旋转,于是力矩将始终朝同一方向。小型直流电动机就是这样制成的。较大型的电动机,无论是直流的或交流的,往往利用一个由电源激励的电磁铁来代替永磁铁。
在认识了电流能够产生磁场之后,人们立即提出,也可以设法使磁铁产生电场。各种实验都尝试过。例如,将两根导线平行排列,当电流通过其中之一时就希望能在另一根导线中也找到电流。当时的想法是:磁场或许会用某种方法在第二根导线中拖动着电子前进,给出诸如“同类喜欢以同样的方式运动”的规律。结果是否定的,尽管已利用了当时可资用的最大电流,以及为探测电流用的最灵敏电流计。把大块磁铁置于导线旁边也产生不出可观测到的效应。最后,法拉第于1840年发现最重要的特点给漏掉了——只有当某种东西正在变化 时电效应才存在。如果两导线之一中存在着正变化着 的电流时,则另一根导线中会有电流感生,或者如果一块磁铁在一电路附近运动 ,则在该电路中会有电流存在。我们讲,这些电流是给感生 出来了。这就是法拉第所发现的电磁感应效应。它把相当沉闷的静场课题转变成包括大量奇异现象的、十分激动人心的动力学课题。本章专为其中某些现象做出定性描述。正如以后将会见到的,人们很快就将遇到难以详细做出定量分析的一些相当复杂的情况。但不要紧,这一章的主要目的首先在于使你熟悉所涉及的现象,我们在以后才做详细分析。
从我们所学过的知识可以容易理解磁感应现象的一个特性,尽管在法拉第时代还没有被人知道。它来自作用于运动电荷的v×B这种力,而该力正比于电荷在磁场中的速度。假设有一根导线在一块磁铁附近经过,如图16-2所示,并将这根导线的两端连接至一电流计。如果移动导线使其通过磁铁的一端,电流计的指针就会摆动。
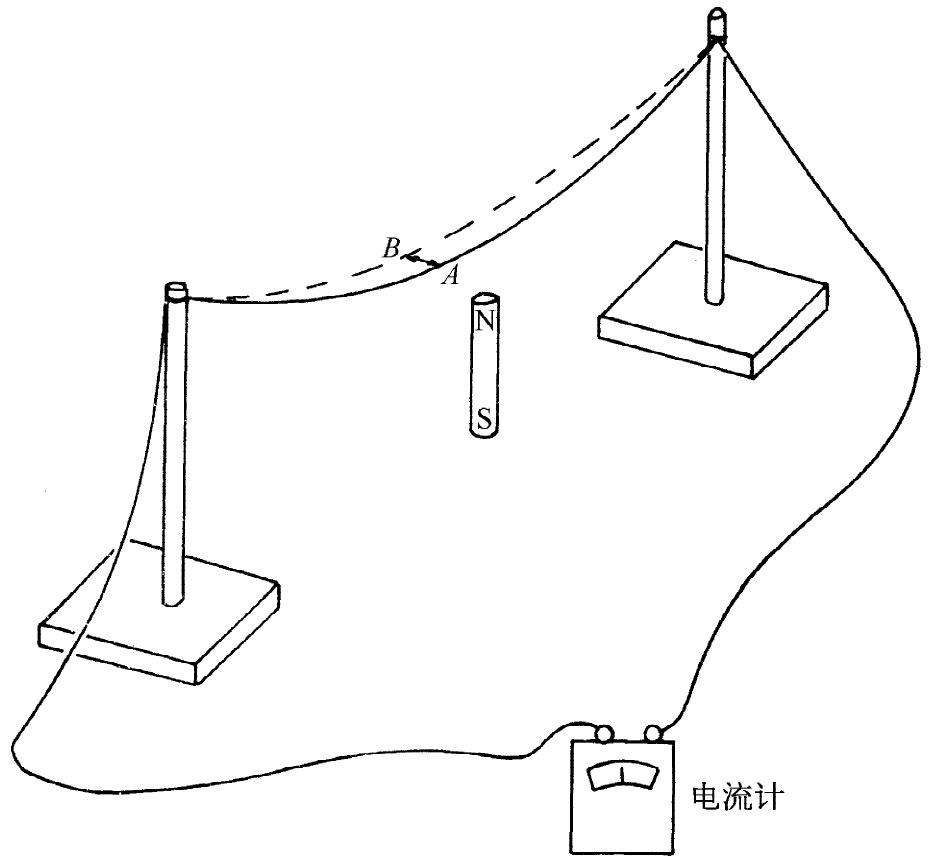
图16-2 一根导线在磁场中运动会产生电流,并由电流计显示出来
磁铁产生了某个竖向磁场,而当我们将导线推过该磁场时,导线里的电子便会感受到一个侧向 力——既垂直于场也垂直于运动。该力沿着导线推动电子。但为什么会使电流计摆动呢,它与那个力相距有那么远?这是由于当那些感受到磁力的电子试图运动时,它们——通过电的排斥——沿导线推稍远的电子,这些被推的电子又依次推斥更远一些的电子,以此类推,在一个长距离上的电子也受到推斥,简直令人吃惊。
最早制成电流计的高斯和韦伯感到如此惊异,以致试图弄清楚这些力在导线中会传到多远。他们把导线跨越整个市区。在一端,高斯先生将导线接至电池组(电池在发电机之前就为人们所熟悉),而韦伯先生则在另一端观察电流计的摆动。于是他们有了一种在长距离上通讯的办法——这就是电报的起源!当然,这并非直接与感应有关,它只是使导线载流必须用的方法,不管电流是不是由感应推动的。
现在假设在图16-2的装备中,我们让导线静止不动而令磁铁运动。这样,仍然会看到在电流计上的效应。正如法拉第所发现的那样,把磁铁在导线下面朝某一方向移动与将导线在磁铁上面朝反向移动,具有相同的效应。但当磁铁被移动时,就不再有作用于导线内部电子上的任何v×B力了。这是法拉第找到的一个新效应。今天,我们也许希望从相对论性的论证中来理解它。
我们已经了解到一块磁铁的磁场是来自它的内部电流。所以如果不用图16-2上的那块磁铁,而是用一个载有电流的线圈,我们预料也会观察到相同的效应。如果使导线运动并经过线圈,则将有电流流经该电流计,或如果让线圈运动并经过导线,情形也是如此。但现在有一个更动人的事态发生了:若我们不是 通过运动而是通过改变其中的电流 变更线圈的磁场,那么在电流计中又再度会发生效应。例如,设有一导线回路放在一线圈附近,如图16-3所示,此时若保持回路与线圈两者都不动,而断开线圈中的电流,就会有一电流脉冲通过电流计。当我们再对线圈通上电流时,电流计则将向相反的方向摆动。
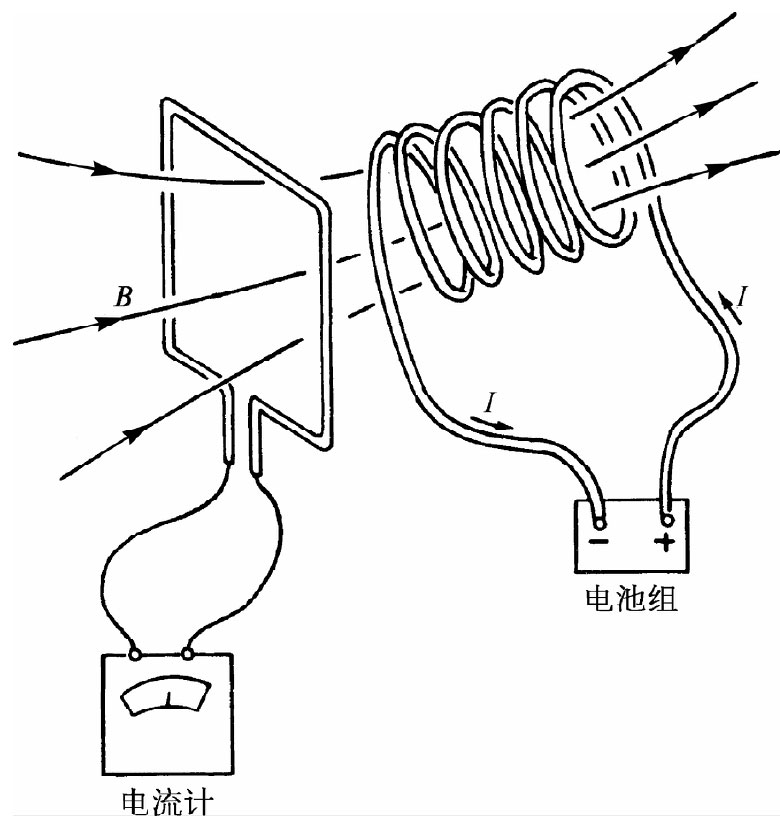
图16-3 如果移动一个载流线圈或将其中的电流变化,这个线圈会在第二个线圈中产生电流
每当在诸如图16-2或图16-3所示情况中电流计有电流通过时,导线里的电子总会受到沿着导线某一方向的一个净推力。在不同位置可能有不同方向的推力,但在某一方向的推力比其他方向的大。这推力绕整个电路的累积是什么,这个净的累积起来的推力叫作该电路的电动势 (emf)。更准确地说,电动势被定义为导线中单位电荷所受的沿线切向力对整个电路环绕一周的路程所作的积分。法拉第的整个发现在于可以由三种不同方法在导线中产生电动势:通过使导线运动,通过使磁铁在导线附近运动,或通过改变邻近导线中的电流。
让我们再考虑图16-1的那部简单机器,只是现在不再输入电流通过导线使之转动,而是由一外力,比如是用手或水轮机使该回路旋转。当线圈转动时,它的导线在磁场中运动,而我们便将在该线圈电路中发现电动势。电动机变成了发电机。
发电机的线圈由于运动就有感生电动势。这电动势大小由法拉第所发现的一个简单法则给出(目前仅陈述这一法则,等待以后再详细分析)。法则是这样的:当穿过回路的磁通量(这通量就是B的法向分量对整个回路所包围面积的积分)随时间变化时,电动势等于这通量的变化率。我们称这一法则为“通量法则”。你看到当图16-1中的线圈转动时,穿过它的通量改变了。开始时有某一通量朝一个方向穿过,然后当线圈转过了180°时相同的通量朝另一个方向穿过。如果继续转动线圈,该通量首先是正,然后是负,再又是正,如此等等。通量的变化率必然也是正负交替地改变的。因而在该线圈中就有一个交变电动势。如果将这线圈的两端通过某种滑动接触——称为汇电环——(只有这样导线才可不至于扭绕起来)与外面导线连接,则我们具有了一部交流发电机。
或者,也可以这样安排:通过某些滑动接触,使在每转动半圈之后线圈端点与外导线之间的连接便反转过来,因而当电动势反转时,连接方式也反转了。因而电动势的脉冲始终在同一方向推动电流通过外电路。这样,我们就有一部所谓的直流发电机。
图16-1上的那部机器既是电动机也是发电机。利用两部结构全同的永磁式直流“电动机”,在它们的线圈间用两根铜线相连,则关于电动机与发电机之间的互易性就可以漂亮地显示出来。当其中一个线圈的轴做机械旋转时,它便成为一部发电机而推动另一部作为电动机。如果将第二部的轴旋转,则它变成发电机而把第一部当成电动机驱动。因此,这里是自然界中新型等效性的一个有趣例子:电动机与发电机彼此等效。事实上,这种定量的等效性并非完全出于偶然,它是与能量守恒律密切相关的。
能够用来既产生电动势又响应电动势的装置的另一种例子,是一部标准电话机的接收器——即“听筒”。贝尔原来的电话机由用两根长导线连接起来的这样两个听筒构成,其基本原理如图16-4所示。一块永磁铁在由软铁制成的两块“轭铁”以及在一薄铁膜片中产生了磁场,该膜片则由声压引起运动。当这膜片运动时,改变了轭铁中的磁场大小。因此,当声波撞击膜片时,在环绕其中一块轭铁的线圈中所穿过的磁通量就改变了。因而在该线圈中就有电动势。如果线圈的两端与一电路相连接,则一种以电的方式表达声音的电流就会建立起来。
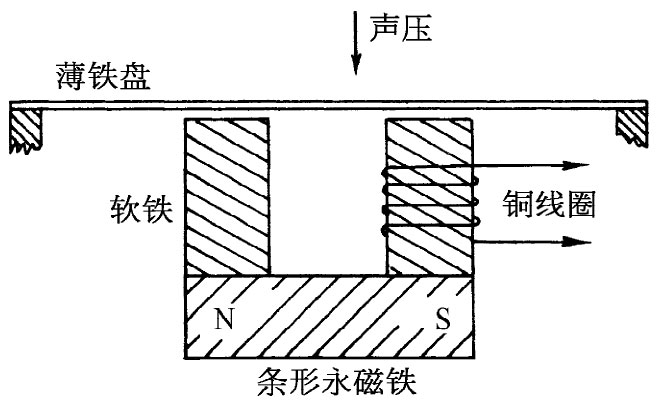
图16-4 电话的送、受话器
如果图16-4的线圈两端用两根导线连接至另一个完全相同的装置,则那变化着的电流将在第二个线圈中流动。这些电流将产生一个变化着的磁场,并将对该铁的膜片造成一个变化的吸引作用。这膜片将上下振动而造成声波,这些声波大体上与原来使膜片振动起来的那些声波相似。这就是说,利用几块铜和铁就能使人们的声音在导线上传递!
(现代的家用电话所用的受话器与上面所描述的相似,而其送话器改进了,它利用了一种新发明以获得较强大的功率。那就是“炭粒传声器”,它利用声压以改变来自电池组的电流。)