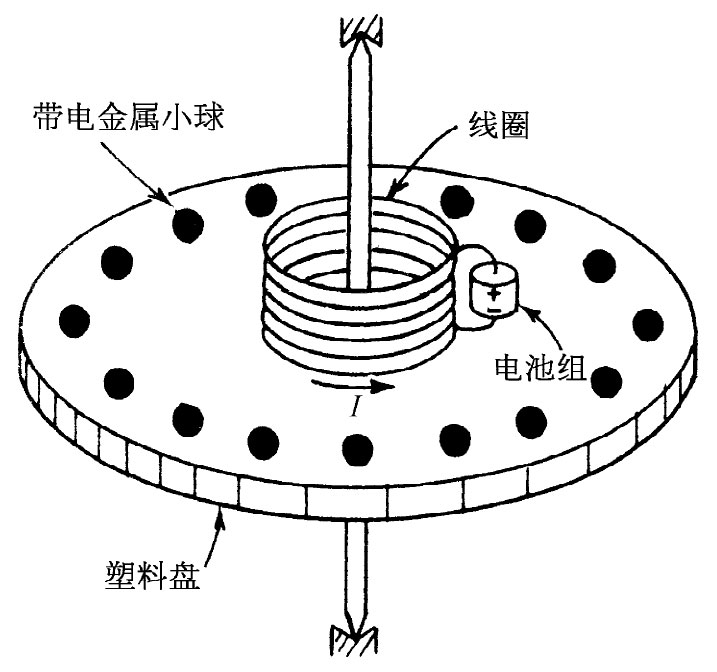
图17-5 如果电流I停止了,该盘是否会转动
现在要向你们描述一个显而易见的佯谬。佯谬指的是这样一种情况,当用一种方法分析时得出一个答案,而用另一种方法分析时又得出另一个答案,因而对于实际上究竟会发生什么我们就会陷于某种困境。当然,在物理学中从未有过任何真正的佯谬,因为实际上只有一个正确答案,至少我们相信自然界只按照一种方式行动(不用说,那就是正确方式 )。因此,在物理学中佯谬只是我们本身理解上的一种混乱。下面是我们将要提出的一个佯谬。

图17-5 如果电流I停止了,该盘是否会转动
试想象构造一个如图17-5所示的装置。一个薄而圆的塑料盘被支撑在一根装有优良轴承的同心轴上,从而能够十分自由地旋转。在该盘上,与转轴同心地放着一个短螺线管形状的线圈。通过这个线圈的恒定电流I由一个同样是装在盘上的小电池组供应。靠近盘的边缘绕圆周边等距离地分布着若干个金属小球,它们相互之间以及与线圈之间均由制造该盘的塑料材料绝缘。这些小导体球,每一个都各带有等量的静电荷Q。每件东西都完全固定,而盘则静止不动。假设现在由于某一偶发事件或由于预先的安排,线圈中的电流被中断了,然而却没有受到任何外界干扰。只要继续通电流,便有或多或少与盘的轴平行的磁通量穿过该线圈。当电流中断时,这通量一定会趋于零。因此,就必然会感生一电场,而这电场将以该轴为中心环绕成一些圆周。在盘的周边那些带电球体均将感到一个与圆盘边缘相切的电场。这个电力对于所有电荷来说都在与圆盘边缘相切的方向,因而将产生一个作用于该盘上的净力矩。从上面的论证,我们预期当线圈中电流消失时,圆盘将开始转动。要是我们已知道盘的转动惯量、线圈中的电流以及小球上的电荷,那我们就能够算出所要的角速度。
但我们也可轻易地做出不同的论证。利用角动量守恒原理,我们可以说,盘及其一切部件的角动量在开始时为零,因而这整套装置的角动量就应该保持等于零。当电流中断时不应有转动。究竟哪一种论证才是正确的呢?盘将转动还是不转动?我们将把这一问题留给你们去思考。
必须提醒你们一点,正确的答案并不有赖于任何非本质的特征,诸如电池组的非对称位置等等。事实上,你可以想象一种诸如下述的理想情况:该螺线管是由超导电线绕成的,里面通有电流。在该盘已经小心地被安置于静止状态后,让螺线管的温度缓慢上升。当导线的温度达到介乎超导电性与正常导电性之间的转变温度时,螺线管里的电流便将因导线的电阻而趋向零。如前所述磁通量将降低至零,因而环绕着该轴心将产生一个电场。我们也应该提醒你,这个解答并不容易得到,但也不是一种诡计。当你把它想出来时,你已经发现了一个重要的电磁学原理。