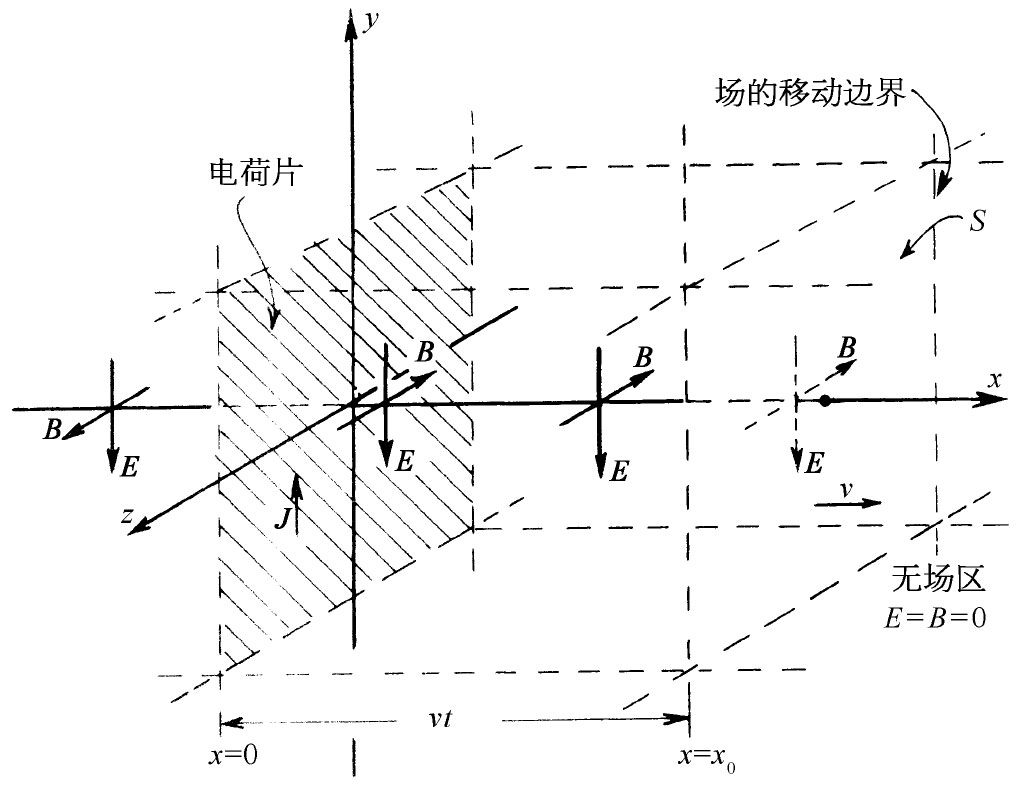
现在就来谈谈一些新的结果。它们是由于将所有的麦克斯韦方程集合在一起而产生的。首先,让我们看看在一个我们选定为特别简单的情况下会发生什么。假定所有的量都仅在一个坐标内变化,我们的问题就变成一个一维问题了。这样的情况如图18-3所示。我们具有置于yz平面上的一片电荷。该片电荷起初是静止的,然后瞬息得到一个平行于y轴的速度v,并保持以这一恒定速度运动。你也许会为有这种“无限大”的加速度而担心,但实际上并不要紧,只要想象该速度很快就提高到v。因此,我们突然就有一个面电流J(J是在z方向的单位宽度中的电流)。为了保持问题简单,我们假定还有一片静止的异号电荷叠加在yz平面上,使得不会发生任何静电效应。并且,虽然在图上我们仅仅表明,在一个有限区域里所发生的情况,但应该想象该片电荷伸展至±y和±z的无限远处。换句话说,我们有这么一种情况,即原本没有电流,但突然有了一个均匀的面电流。这样将发生什么呢?

图18-3 一个无限大电荷片突然平行于其本身运动。这样就会有磁场和电场以一恒速率从该片传播出去
噢!当沿正y方向上有一片电流时,如我们所知,在x>0的地方就会产生一个沿负z方向的磁场,而在x<0的区域磁场则沿相反方向。我们可以通过应用磁场的线积分将等于电流除以∈0 c2 这一事实来求出B的大小。这样,就会得到B=J/(2∈0 c2 )(因为在一宽度为w的长片上,电流I就是Jw,而B的线积分则为2Bw)。
这向我们提供了在该片附近——即对于小x处——的磁场,但由于我们所设想的乃是一个无限大的片,因而也会期望这同样的论证应当给出在较大x值即在较远处的磁场。可是,这就意味着,接通电流的瞬间,磁场突然处处从零变到一个有限值。但请等一下!如果磁场突然改变,也会产生巨大的电效应(只要 它在改变,就有电的效应)。由于移动了该电荷片,因此,我们造成一个变化的磁场,因而电场也一定被产生。如果有电场产生,则它们必定从零开始而变化至某一个量值。这样就将有个∂E/∂t,与电流J一起将对磁场的产生做出贡献。因此,通过存在大量交相混合的各个方程求解时,我们不得不力图同时求解所有的场。
如果仅仅考察麦克斯韦方程组,还不容易直接看出如何去求得解答。因此,我们将首先向你们说明答案是什么,然后才证实它的确满足那些方程。答案是这样的:上面我们所算出的场B,实际上的确是在该电流片右面附近(即对于小x值)产生的。结果一定是这样,因为如果环绕该片做一个小回路,则不会有地方可供任何电通量穿过。但是在较远——x较大——处的B场起初为零,它保持了片刻为零,然后便突然增大。总之,我们一开通电流,磁场立即靠紧在它的地方跃升至一恒定值B,然后这个B的跃升又从源区再度扩展出去。经历了某一段时间后,在某一x值之内就将处处有一个均匀强磁场,在更远的地方则都等于零。由于对称的缘故,它会朝着正的和负的两个x方向扩展出去。
E场也与此一样。在t=0(当我们开通电流时)之前,场处处为零。然后在经历了时间t之后,E和B两者在扩展到x=vt的范围内都是均匀的,而再往外则均为零。这些场像潮汐波一样向前扩展,其波前以一匀速前进,这速度最终将弄清楚是c,但暂时我们却只叫它作v。关于E或B的大小与x的关系曲线,在t时刻的表现如图18-4(a)所示。再回顾一下图18-3,在t时刻,在x=±vt的区域内都“充满”着场,但这些场却还未到达更远的地方。这里要再次强调,我们是在假定该电流片以及由此产生的场E和B,都是在y和z方向上伸展至无限远的(我们不能够画出一张无限大的片,因而图中所示的只是在一个有限大范围内所发生的事情)。
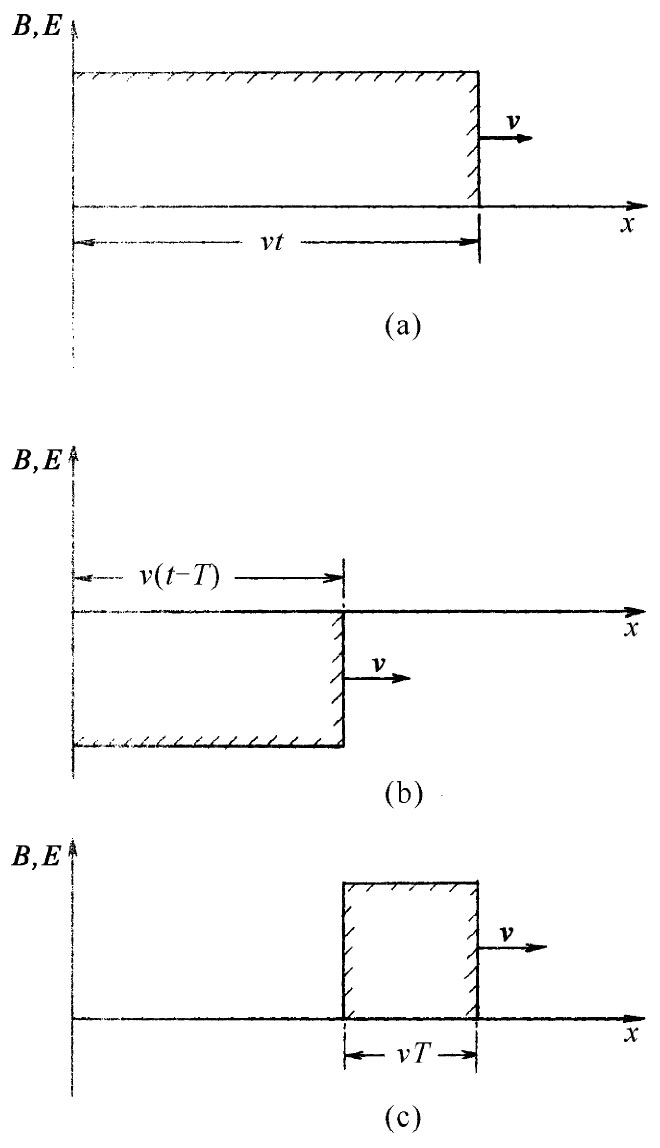
图18-4 (a)在电荷片已经运动之后,在t时刻作为x函数的B(或E)的大小;(b)在t=T时才将一电荷片朝着负y方向移动后的场;(c)(a)与(b)之和
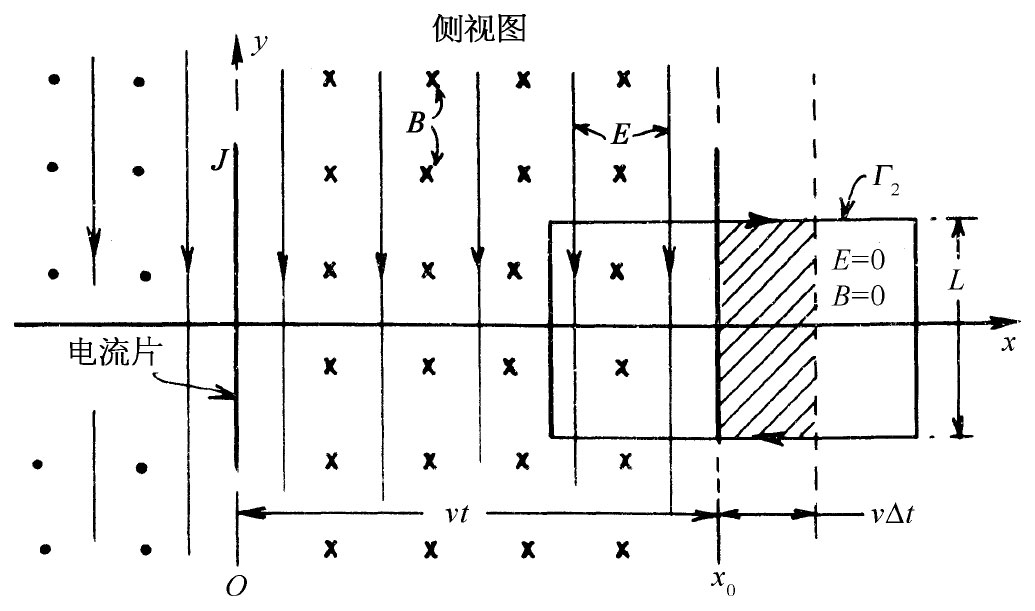
现在,我们要对所发生的情况做定量分析。为此,就要考察两个截面图,一个是沿y轴向下的俯视图,如图18-5所示;另一个则是沿z轴往回望的侧视图,如图18-6所示。我们从该侧视图开始,就会见到该电荷片正在向上移动,在+x各处磁场都指向书内;而在-x各处磁场则指向读者,电场处处向下——一直伸展至x=±vt处。

|
|
| 图18-5 图18-3的俯视图 | 图18-6 图18-3的侧视图 |
让我们看看这些场是否符合麦克斯韦方程组。首先,画出一条供计算线积分用的回路,比如说图18-6中所示的那个矩形Γ2 。你会注意到,这矩形的一边落在有场的区域,但另一边却落在场还没有到达的地方。有一些磁通量穿过这一回路。如果这通量正在变化着,则环绕该回路应有电动势。如果波前正在前进,就会有一个变化着的磁通量,因为B所存在的区域正在以速度v逐渐扩大。在Γ2 内的通量等于B乘以存在磁场的那一部分面积。由于B的大小恒定,所以通量的变化率就等于B的量值乘以面积的变化率。要获得面积的变化率挺容易。若该矩形的宽度为L,则其中有B存在的面积在时间Δt内将改变LvΔt(见图18-6)。于是通量的变化率便是BLv。按照法拉第定律,这应等于E环绕Γ2 的线积分,而那恰好就是EL。于是我们就有方程:
E=vB. (18.10)
因此,若E对B的比率为v,则我们所假设的这些场都将满足法拉第方程。
但那不是唯一的方程,我们还有联系着E和B的另一个方程:

为了应用这个方程,我们考察图18-5那个俯视图。我们已经知道,这一方程将提供靠近该电流片的B值。并且,对于任何画在该片之外但在波前之后的回路,就不会有B的旋度,也不会有任何j或变化的E,因而方程式(18.11)在那里是正确的。现在让我们来看看对于如图18-5所示的那条与波前相交的回路Γ1 发生什么事情。这里并没有电流,因而方程式(18.11)可以——用积分形式——写成
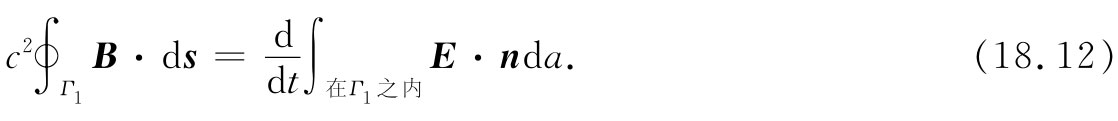
B的线积分恰好就是B乘以L。E通量的变化率仅仅是由前进的波前引起的。在Γ1 内E不为零的面积正在以vL的速率增大,于是式(18.12)的右边就是vLE,所以该方程式变成
c2 B=Ev. (18.13)
我们有这么一个解:即在波前后面B和E都是恒量,它们各与波前行进的方向垂直而且彼此之间也互相垂直。麦克斯韦方程组规定了E对B的比值。根据式(18.10)和(18.13),得

可是请等一等!我们已求得关于比值E/B的两个不同 的条件。刚才描述的这种场能否确实存在呢?当然,要使这两个式都正确,只能有一个速度v,也即v=c,波前一定要以速度c前进。这样我们就有了一个例子,其中来自电流的电效应以某个有限速度c传播。
现在试问,如果在经历了一段短时间T之后,突然把电荷片的运动停止下来,会发生什么情况呢?应用叠加原理我们能够看出将发生什么事情。我们有过电流原来为零,然后才突然开通的情况,并且已知道了那种情况的解。现在我们打算加上另一组场,即取另一片电荷,并仅在开通了第一个电流后的时刻T,在相反的方向以相同的速率突然使它开始移动。这两者相加起来的总电流起初为零,然后接通了一段时间T,之后又再中断——因为两电流恰好互相抵消,于是我们有一个电流的矩形“脉冲”。
这一新的负电流产生了与正电流相同的场,只是所有的符号都相反,当然都延迟了时间T。波前再次以速度c传播出去,在t时刻它已到达了x=±c(t-T)的远处,如图18-4(b)所示。因此,就有两“块”场以速率c向外推进,正如图18-4的(a)和(b)两部分所示。至于联合场则如图18-4(c)所示,在x>ct处场为零,在x=c(t-T)与x=ct之间场为恒量(具有我们上面所求得的值),而在x<c(t-T)处场又是零。
总之,我们有一小块场——厚度为cT的一块——离开了该电流片而独自穿越空间传播。场已经“起飞”了,它们正在自由地穿越空间传播着,不再与源有任何方式的联系。毛虫已变成了蝴蝶!
这组电磁场如何能维持它本身呢?答案是:依靠法拉第定律▽×E=-∂B/∂t和麦克斯韦新项c2 ▽×B=∂E/∂t的联合效应。它们不得不维持其本身的存在。假定磁场已在消失,那就会有一个变化着的磁场,而这变化着磁场会产生一个电场。如果这个电场试图消逝,则这变化着的电场将再度产生磁场。因此,通过不断的相互影响——通过由一个场到另一个场的前后快速变换——它们必定会永远继续下去,而绝不会消逝 [1] ,它们以一种舞蹈方式——一个围着另一个,第二个又围着第一个转——把它们自己维系在一起,穿越空间而向前传播。