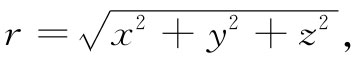
我们已看到波动方程具有与平面波相对应的解，而任何电磁波都可描述为许多平面波的叠加。然而，在某些特殊情况下，用不同的数学形式来描写波场更为方便。现在，我们很想讨论球面波——与从某一中心扩展开去的球形表面相对应的波——的理论。当你把一块石头扔到湖里时，那些涟漪会在水面上以圆形波的形式扩展开去——它们是二维波。球面波与此相似，只不过它是在三维中扩展出去而已。
在我们开始描述球面波之前，需要一点数学。假设有一个函数仅取决于离某一原点的径向距离r——换句话说，这是一个球对称的函数，让我们叫它函数ψ（r），其中r是指
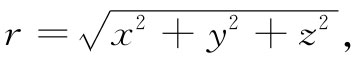
即与原点间的径向距离。为了求出满足波动方程的函数ψ（r），我们将需要关于ψ的拉普拉斯表示式。因此，就要求出ψ对x，y和z的二次微商之和。我们将采用这种符号，即ψ′（r）代表ψ对r的微商，而ψ″（r）代表ψ对r的二次微商。
首先，求对x的微商。第一次微商为
因此，ψ对x的二次微商就是
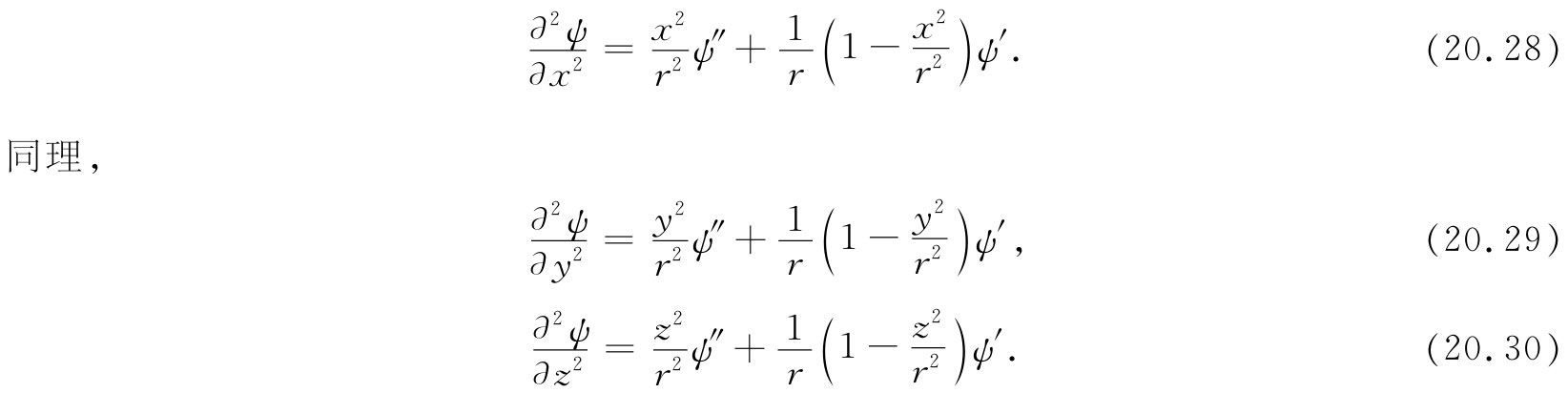
拉普拉斯算符等于这三个微商之和。记住x2 +y2 +z2 =r2 ，我们便得
把这一方程写成如下形式往往更为方便：
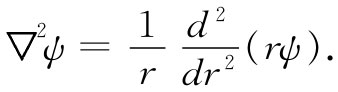（20.32）
如果你将式（20.32）中所标明的微分算出，则将看到右边与式（20.31）的右边相同。
如果希望讨论能够像球面波那样传播出去的球对称场，则场量就必须是r与t两者的函数。这时，假如我们问起下列三维波动方程
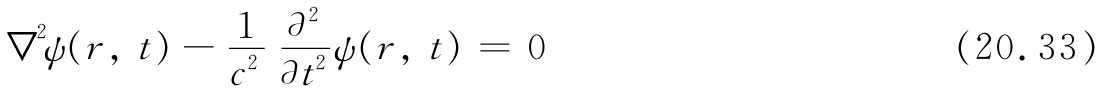
之解是怎样的函数ψ（r，t）。由于ψ（r，t）仅仅通过r而依赖于空间坐标，因而可以采用上面求得的那个拉普拉斯算符方程式（20.32）。然而，为了准确起见，由于ψ也是t的函数，所以我们应该把对r的微商写成偏微商。这样该波动方程便变成
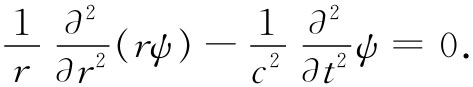
现在我们必须解出这一方程，这看来比平面波的情况复杂得多。可是注意，如果我们以r乘这一方程，则得到
上式告诉我们，函数rψ满足以r为变量的一维波动方程。应用曾经经常强调过的普遍原理，即相同的方程总会有相同的解，那么我们知道，如果rψ仅仅是（r-ct）的函数，则它将是方程式（20.34）的解。因此，我们就知道球面波一定具有下面这种形式：
rψ（r，t）=f（r-ct）.
或者，正如我们以前曾见过的，同样可以说rψ可能具有这种形式：
rψ=f（t-r/c）.
两边各除以r，便得到场量ψ（不管它可能代表什么）具有如下形式：
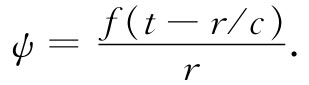（20.35）
这样一个函数表示从原点以速率c传播出去的普遍的球面波。如果暂时忘却那个在分母上的r，则在某一给定时刻波幅作为离原点距离的函数会具有一定形状并以速率c向外传播。然而，那个分母中的因子r却说明当波传播时波幅正比于1/r减小。换句话说，和平面波不同，当平面波向前行进时波幅维持不变，而在一球面波中波幅却是恒定地减小，如图20-6所示。这一效应不难从简单的物理论证得到理解。
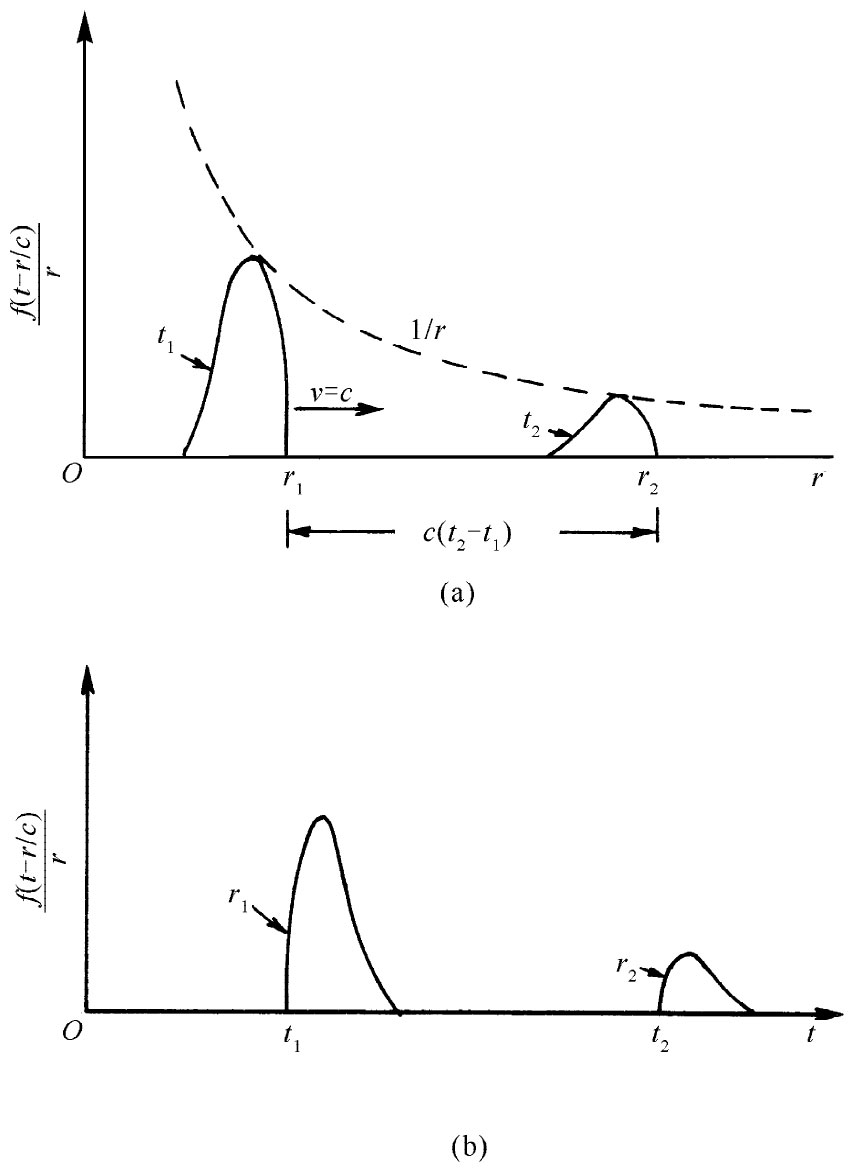
图20-6 球面波ψ=f（t-r/c）/r。（a）作为r函数的ψ在t=t1 时刻的情况和同一个波在一个较后时刻t2 时的情况；（b）作为t函数的ψ在r=r1 处的情况和同一个波在r2 处所看到的情况
我们知道，波的能量密度取决于波幅的平方。当波向外传播时，其能量分布在与径向距离的平方成正比的越来越大的面积上。如果总能量守恒的话，则能量密度必定随1/r2 下降，而波幅则一定随1/r减小。因此，式（20.35）是关于球面波的“合理”形式。
我们已忽略了对于一维波动方程的第二种可能解：
rψ=g（t+r/c）
或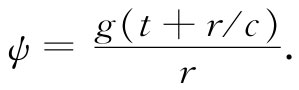 
这也代表一个球面波，不过是一个从较大的r朝着原点向内 传播的波。
现在打算做一个特殊假定，但不做任何证明。我们讲，由源所产生的波仅是向外 行进的波，由于我们知道波是由电荷的运动所引起的，所以我们认为波是从电荷那里向外发出来的。要想象在电荷还未开始运动以前就有一个球面波从无限远处出发而恰恰在那些电荷刚要开始动起来的那一瞬到达它们那里，这应该是相当奇怪的。虽然这是一个可能的解，但经验表明，当电荷被加速时波是从电荷那里向外传播的。尽管麦克斯韦方程组会允许这两种可能性，但我们还要放进一个附加事实 ——基于经验——只有向外行进波的解才产生“物理意义”。
然而，也应该指出，对于这一附加假设存在一个有趣的后果：我们正在消除存在于麦克斯韦方程组中的时间对称性。关于E和B原来的方程组，以及从它们导出的波动方程式，都具有这么一种性质，即如果改变t的符号，方程式仍将保持不变。这些方程表明，对应于沿某一方向行进波的每一个解，就有一个沿相反方向传播的波作为同样有效的解。我们关于将只考虑向外的球面波的陈述是一个重要的附加假设（一种旨在避免这一附加假设的电动力学表达方式已由人们仔细地研究过。令人惊异的是，在许多场合下它并未 在物理上导致荒谬的结论，但若此刻就来讨论这些想法，那就可能把我们引入歧途太远了。我们将在第28章对它们稍微多讨论一些）。
必须提出另一要点。在一个向外行进波的解即式（20.35）中，函数ψ在原点处等于无限大。那是有点特别的。我们很想有一个处处平滑的波动解。但我们的解必须在物理上代表某个源位于原点的情况。换句话说，由于疏忽我们已犯了一个错误。我们并未处处 对自由波动方程式（20.33）求得解答，只是求得了在其右边除了原点之外处处都为零的方程式（20.33）的解。我们所以会不知不觉犯错，是由于在上述求导过程中，在r=0的某些步骤是不“合法”的。
让我们来证明，在静电问题中也很容易犯同样类型错误。假定要求出自由空间里静电势方程▽2 ϕ=0的解。这拉普拉斯方程所以等于零，是因为我们假设处处都没有电荷。但关于这一方程的一个球对称解——即仅仅取决于r的某个函数ψ——将会怎么样呢？利用式（20.32）关于拉普拉斯算符的公式，就有
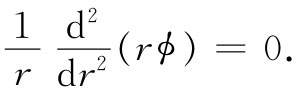
对上式乘以r，便得到一个易于积分的微分方程：
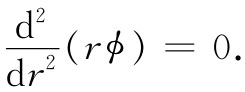
如果对r积分一次，就求得rϕ的一次微商为一常数，我们可称之为a：
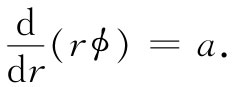
再积分一次，求得rϕ的形式为：
rϕ=ar+b，
其中b是另一积分常数。因此，我们发现，下列ϕ是自由空间中静电势方程的一个解：
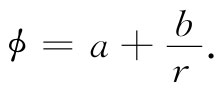
显然出现了某种差错。在不存在电荷的区域中，我们知道静电势的解为：势处处为恒量。这相当于我们解中的第一项，但还有那第二项，这说明有一个与离原点的距离成反比变化的势的贡献。然而，我们知道，这样一个势相当于在原点处有一个点电荷。所以，虽然我们当初设想对自由空间中的势求解，但上述的解却也给出了在原点上有一个点源的场。你是否看到目前所发生的事情与上面我们对波动方程求球对称解时所发生的事情之间存在的相似性？要是真的在原点上没有任何电荷或电流，那么就不会有任何往外跑的球面波了。当然，球面波一定是由原点处的源产生的。在下一章中我们将探讨那些正在往外行进的电磁波与产生了这些波的电流和电压之间的关系。
[1] 参考：第一卷47章声，波动方程；第一卷28章，电磁辐射