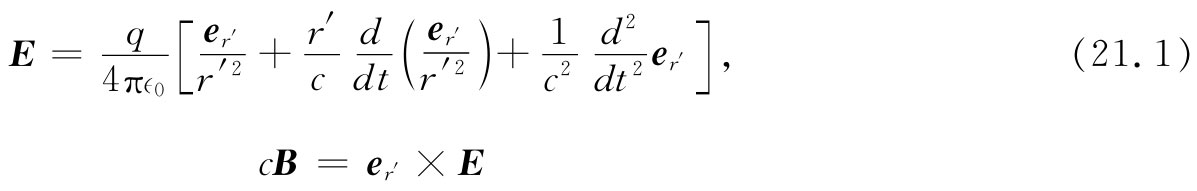
在上一章我们看到,在麦克斯韦方程组的解中就有电与磁的波。这些波相当于无线电波、可见光、X射线等现象,视波长如何而定。我们曾在第1卷中详尽地学习过光学。本章将把这两门学科互相结合起来——证明麦克斯韦方程组确实能够形成我们前期处理光学现象的基础。
过去当我们学习光学时,是由写出一个以任意方式运动着的电荷所产生的场的方程开始的,即
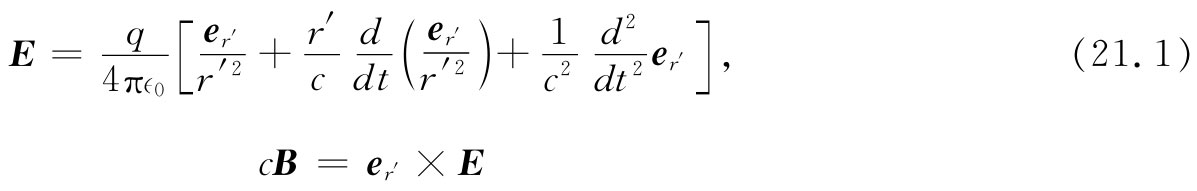
[见第1卷式(28.3)及式(28.4)。正如下面所述,这里的符号是原来符号的负值。]
如果电荷是以任意方式运动,则我们现在 在某一点所求得的电场并非取决于电荷此刻所处的位置和运动,而仅仅取决于在一个较早 时刻——早于光以速率c从电荷传播至该场点的距离r′所需的时间的那个时刻——的位置和运动。换句话说,若要得到t时刻在点(1)处的场,就必须算出在(t-r′/c)时刻电荷所处的位置(2′)及其运动,其中r′是在(t-r′/c)时刻从电荷位置(2′)至点(1)的距离。加上一撇是为了说明r′是从点(2′)至点(1)的所谓“推迟距离”,而非电荷在t时刻的位置即点(2)至该场点(1)的实际距离(见图21-1)。注意,现在我们正在采用一种关于单位矢量er 方向 的新规则。在第1卷第28和34两章中我们曾取r(因而er )指向 源处,那是方便的。但现在却要按照上面关于库仑定律的定义,其中r是从 点(2)处的电荷指向 点(1)处的场点的。当然,唯一不同之处是,现在的新r(和er )就是过去那些量取负值。
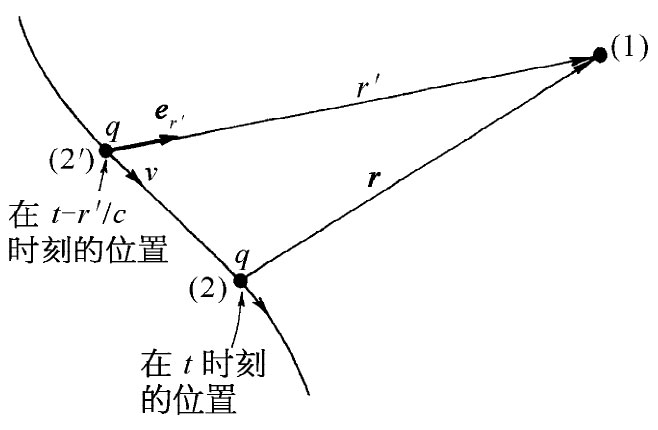
图21-1 t时刻在点(1)处的场取决于在(t-r′/c)时刻电荷q所占据的位置(2′)
我们也已知道,若电荷的速度v总是比c小得多,而且只考虑那些距离电荷很远的点,以致只有式(21.1)中最后一项才算重要,则场也就可以写成

和 cB=er′ ×E.
让我们稍微详细地考察一下整个公式(21.1)讲些什么。矢量er′ 乃是从推迟位置(2′)至点(1)的单位矢量。那么第一项是我们预期的在推迟位置处的电荷的库仑场,可以把它叫作“推迟库仑场”,电场与距离的平方成反比,并且从电荷的推迟位置上指向外(也就是在er′的方向上)。
但那只是第一项。其他两项告诉我们,电学定律并未 讲过除了推迟场外所有场都与静场相同(这是人们有时喜欢说的)。对于“推迟库仑场”我们还必须加上其他两项。式中的第二项讲,对于推迟库仑场有一项“修正”,那就是推迟库仑场的电荷变化率 乘以延迟时间r′/c。在某种意义上,这一项势必对第一项的推迟做出补偿 。这前面两 项相当于在算出了“推迟库仑场”之后再把它往后推r′/c这个量,即一直推至时刻t !这一外推是线性的,好像我们必须假定“推迟库仑场”应该以电荷在点(2′)处所算得的变化率继续变化。如果场变化得很慢,则推迟效应几乎完全被修正项所抵消,而这两项一起给我们提供了“瞬时库仑场”那样的电场——也就是在点(2)处的电荷的库仑场——趋向于很好的近似。
最后,式(21.1)中还有第三项,它是对单位矢量er′ 的二项微商。在学习光学现象时我们曾利用过这样的事实,即在离电荷很远的地方,前两项都与距离的平方成反比,因而对于巨大的距离来说,它们比起随1/r减少的第三项来就变得十分微弱。因此,我们完全把注意力集中在这第三项上,并证明(又是对于大距离而言)这一项与电荷的加速度在视线上的垂直分量成正比(并且,我们在第1卷中的大部分工作都是考虑其中电荷正在做非相对论性运动的情况,仅在第36章中才考虑过相对论性效应)。
现在应该尝试把这两件事联系起来。我们既有麦克斯韦方程组,也有关于点电荷场的方程式(21.1),肯定会问这两者是否等效。若我们能从麦克斯韦方程组导出式(21.1),则我们将确实懂得光学与电磁学间的关系。建立这种关系是本章的主要目标。
事实证明,我们不想完全解决这个问题——数学的细节变得过于复杂以致我们不能将其彻底完成。但将进行到足够接近完成的地步,以便使你们能够轻而易举地看出如何才能把联系建立起来,所遗漏的部分将只是一些数学细节。你们当中有些人可能会发觉这一章中的数学相当复杂,因而也就不愿意非常仔细地领会这种论证了。然而,我们认为这样做是十分重要的,即要把你以前学到的与现在正在学习的东西联系起来,或者至少指出这种联系如何才能建立。倘若你对以前各章大致看一看,你就会注意到,每当我们把一种说法作为讨论的起点时,总是要小心地解释它是某个“基本规律”的一种新的“前提”,还是最终可以从别的某些规律推导出来的结果。多亏你们对这些演讲的热切心意,我们才来建立光与麦克斯韦方程组之间的关系。若在某些地方变得太困难,噢,那就是生活——没有其他别的途径可走。