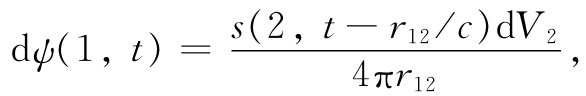
我们已求得关于点源方程式(21.7)的解。下一个问题是:对于一个分布源来说其解是什么呢?那是容易求得的;可以把任何源s(x,y,z,t)都想象为由许多个“点”源所组成,而对于每个体积元dV就有一个其源强为s(x,y,z,t)dV的“点”源。由于方程式(21.7)是线性方程,所以合成场就等于所有这种源的基元产生的场的叠加。
利用上一节的结果[式(21.13)]我们知道,在t时刻在点(x1 ,y1 ,z1 )——或简称点(1)——处的来自点(x2 ,y2 ,z2 )——或简称点(2)——的一个源的基元sdV的场dψ由下式给出:
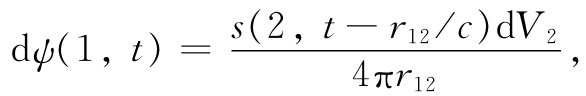
式中r12 是从(2)至(1)的距离。把来自源所有部分的贡献都相加起来,那意思当然是指对所有s≠0的区域进行积分,因而我们有
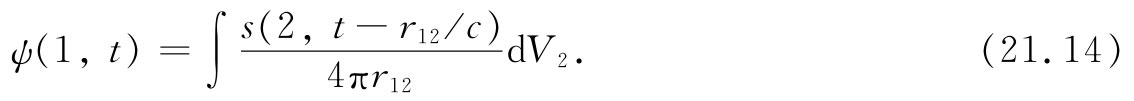
这就是说,在t时刻在点(1)处的场是在(t-r12 /c)时刻离开位于(2)处的各个源的基元的球面波之和。这就是对于任何一组源的有关波动方程的解。
现在我们来看看如何才能得到麦克斯韦方程组的通解。若ψ指的是标势ϕ,则源函数s便变成ρ/∈0 。我们也可以令ψ代表矢势A的三个分量中的任一个,同时由j/(∈0 c2 )的对应分量来取代s。这样,若我们对各处的电荷密度ρ(x,y,z,t)和电流密度j(x,y,z,t)都已知道,则可立即把式(21.4)和(21.5)两方程的解写出来。它们是
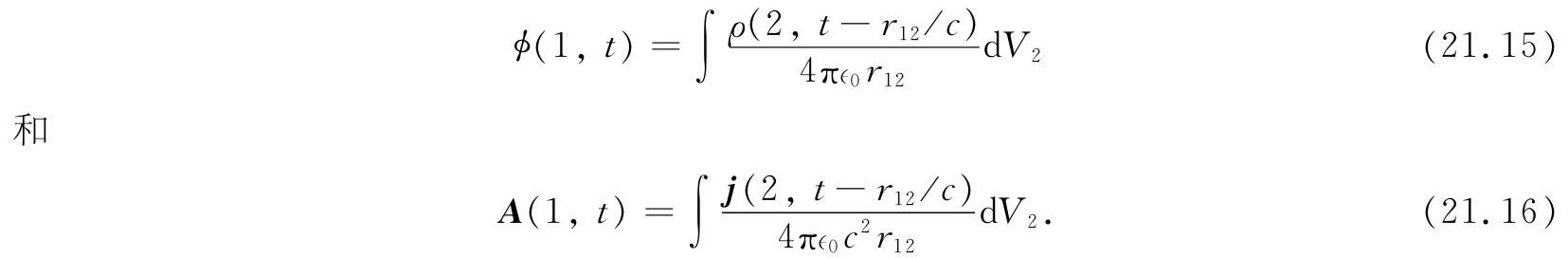
于是利用式(21.2)和(21.3),场E和B便可以通过势的微商而求得[顺便提一下,我们有可能核实由式(21.15)和(21.16)得到的ϕ和A的确满足方程式(21.6)]。
我们已解出了麦克斯韦方程组。在任何情况下,如果给出电流和电荷,便能够从这些积分直接求得势,然后通过微分而获得场。因此,我们已经学完了麦克斯韦理论。而且这也使我们能够把这一个环节与光的理论衔接起来,因为要联系到我们以前关于光方面的工作,所以只需要算出来自运动电荷的电场。尚待做的就是取一个正在运动的电荷,从这些积分算出各个势来,然后再通过微分而由-▽ϕ-∂A/∂t找出E,这样就会得到式(21.1)。事实证明,需要做的工作很多很多,但那是原则。
因此,这里是电磁领域的中心——电和磁,以及光的完整理论;对于由任何运动电荷所产生的场的完整描述;以及另外的一些,全都在这里了。这里就是由麦克斯韦建立起来的、以它的全部功能和美丽而使其完满的建筑物,它可能是物理学中最伟大的成就之一。为要使你想起它的重要性,我们将把它全都收集在一个精致的框架中。
