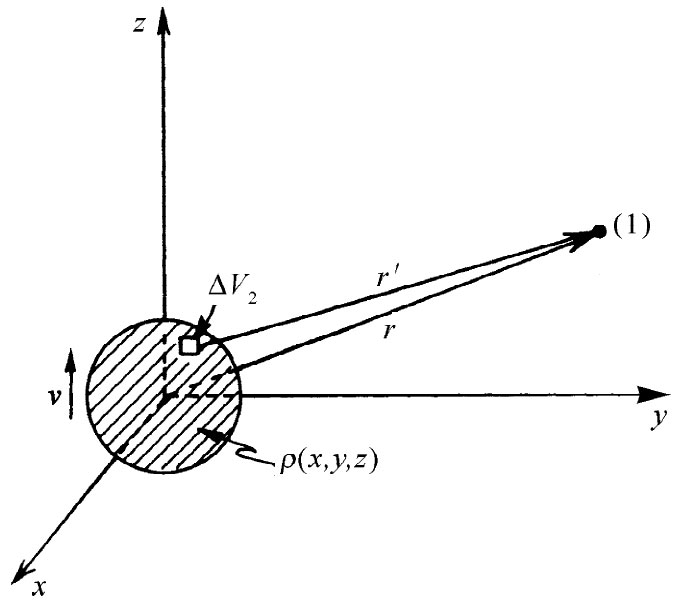
图21-2 点(1)处的势由对电荷密度ρ的积分给出
导出一个运动的点电荷的场公式(21.1)的这个诺言,我们迄今还未曾实现。即使是已有的一些结果,但要把它导出来仍是一件相当复杂的事情。除了在这本讲义的第1卷之外,我们从未在已经发表的文献的任何地方找到过式(21.1) [1] 。因此,你可以看出它不容易导出(当然,一个运动电荷的场已经被写成许多种互相等价的其他形式)。这里,我们不得不把自己限制在几个例子中,这正是为了证实式(21.15)和(21.16)会给出与式(21.1)相同的结果。首先,将证明式(21.1)只在带电粒子的运动是非相对论性的条件下才给出正确的场(仅仅这一特殊情况就能处理我们过去关于光学方面所谈及的90%或更多的内容)。
我们考虑一小团电荷在一个小区域里以某种方式运动的情况,并将找出在远处的场。换一种说法,就是我们正在寻找距离点电荷任意远处的场,而该点电荷正以很小的幅度上下振动。由于光往往从诸如原子那种中性物体内发射出来,所以我们将认为摆动电荷q是处在一个静止不动的等值异号电荷附近。如果这两电荷中心间的距离为d,则这两电荷将具有偶极矩p=qd,这我们将认为是时间的函数。现在应该期待,如果靠近电荷对场进行观察,便无需担心那个推迟效应,电场将与我们以前对静电偶极子所算出的场完全相同——当然,要用到瞬时偶极矩p(t)。但若我们离开得很远,则应该在场中找到一项,它按1/r下降而又依赖于与视线垂直的电荷加速度。让我们来看看是否会得到这样的结果。

图21-2 点(1)处的势由对电荷密度ρ的积分给出
利用式(21.16)由算出矢势A开始。假设运动电荷处于一小团内,其中的电荷密度由ρ(x,y,z)给出,而在任一时刻整团东西以速度v运动,那么电流密度j(x,y,z)就等于vρ(x,y,z)。为了将来方便选取我们的坐标系使z轴指向v的方向,这时问题的几何结构就如图21-2所示。现在要求下面的积分:
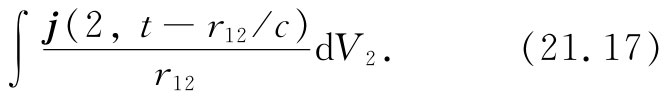
若电荷小团的尺度比起r12 来确实很小,那么可令分母中的r12 等于r,即到该小团中心的距离,并把r取出积分符号之外。其次,也要令该式分子中r12 =r,尽管这实际上并不完全正确。其所以不对,是因为我们在小团的顶端取j与在该小团的底部取j在时间方面稍微有点不同。当在j(t-r12 /c)中令r12 =r时,我们是在同一个时刻(t-r/c)对整个小团取电荷密度。那只有当电荷的速度v远比c为小时才算是良好的近似。因此,我们正在做一种非相对论性计算,用ρv来代替j,积分式(21.17)便变成

由于所有电荷都有相同的速度,这个积分正好是v/r乘以总电荷q。但qv恰好就是∂p/∂t,即电偶极矩的时间变化率——那当然必须是在推迟时刻(t-r/c)算出来的。我们将把它写成ṗ(t-r/c)。因此对于矢势来说就得到

上述结果表明:变化偶极子中的电流会产生一个矢势,这矢势具有源强度为ṗ/(∈0 c2 )的球面波的形式。
现在就可以由B=▽×A得到磁场。由于ṗ完全在z方向上,所以A只有一个z分量;在它的旋度中只有两个不等于零的微商。因此,Bx =∂Az /∂y及By =-∂Az /∂x。让我们首先来考察Bx :
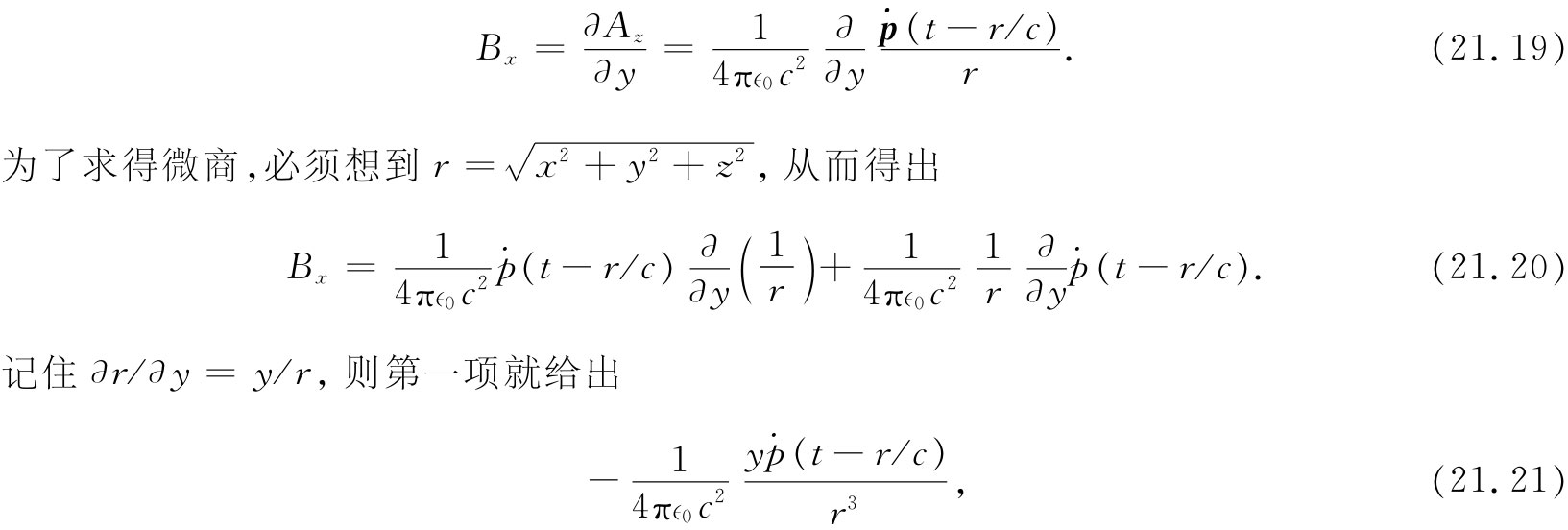
这类似于一个静态偶极子的势,随1/r2 而下降(因为对于给定的方向来说,y/r是个常数)。
式(21.20)中的第二项为我们提供一些新的效应。在进行微商后得
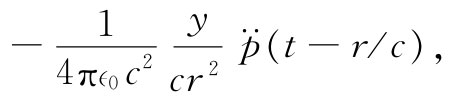 (21.22)
(21.22)
式中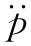 当然是指p对时间的二次导数。这一项来自对式中分子的微商,它是造成辐射的主要原因。首先,它描述了一个仅按1/r随距离下降的场。其次,它取决于电荷的加速度
。你可能开始明白,我们是如何打算得到一个像式(21.1′)那样的结果,而它是描述光辐射的。
当然是指p对时间的二次导数。这一项来自对式中分子的微商,它是造成辐射的主要原因。首先,它描述了一个仅按1/r随距离下降的场。其次,它取决于电荷的加速度
。你可能开始明白,我们是如何打算得到一个像式(21.1′)那样的结果,而它是描述光辐射的。
让我们稍微详细一点检查一下这个辐射项是如何得来的——它是这么一个有趣而又重要的结果。由表示式(21.18)开始,它具有1/r的依存关系,因而除了式中分子上的那个推迟项外就像一个库仑势了。那么,当我们为获得场而对空间坐标取微商时,为什么并不恰好得到1/r2 的场——当然还会有那相应的时间推迟?
按照下述办法我们就能够看出其所以然:如让偶极子作正弦式上、下振动,那么就会有
p=pz =p0 sinωt
和 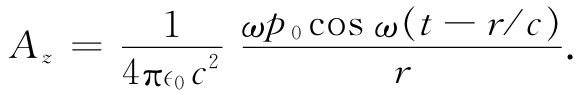
若在某一给定时刻把作为r函数的Az 画成图,则可获得如图21-3所示的那种曲线。该峰的振幅会随1/r减小,但除此之外在空间还有一受1/r的包络线调制的振动。当我们对空间取微商它们将与该曲线的斜率 成正比。从图中我们看出有一些斜率比1/r曲线本身的斜率要峻峭得多。事实上,对于某一给定频率来说,那些峰的斜率显然正比于随1/r变化的波的振幅。因此,这就说明了该辐射项的下降率。
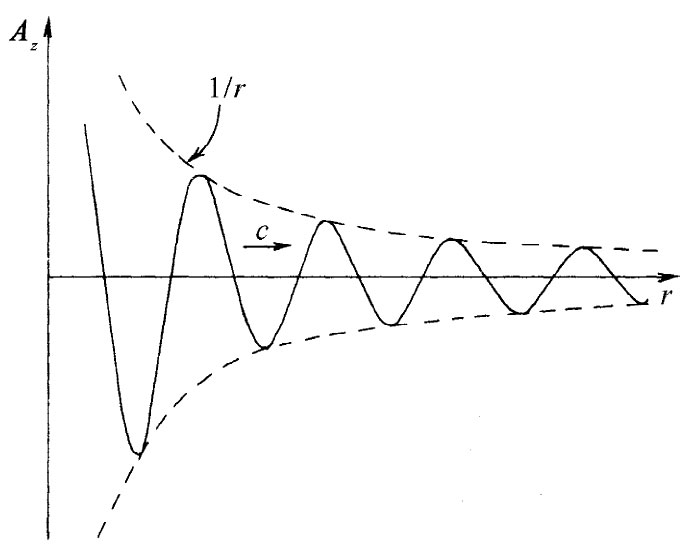
图21-3 对来自一振荡偶极子的球面波,在t时刻矢势A的正分量作为r函数而画成的图
事情的发生完全是由于当波向外传播时源对时间 的变化已变换成在空间里 的变化,而磁场则是取决于势的空间 微商。
让我们回过来完成对磁场的计算。关于Bx 已有式(21.21)和(21.22)两项,因而
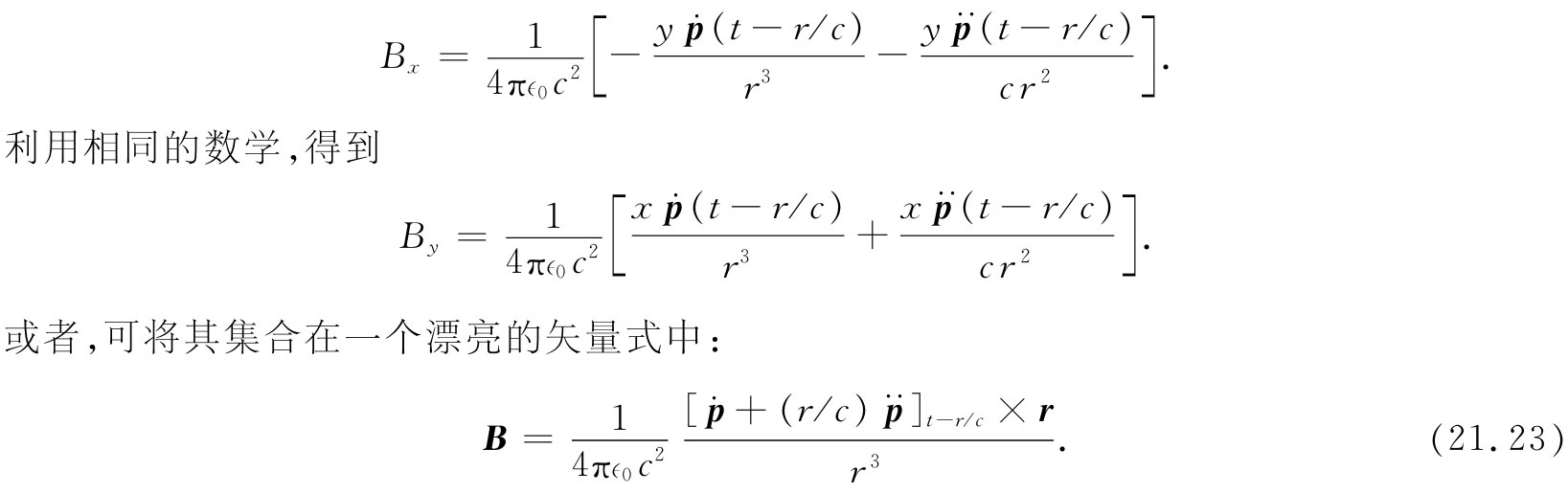
现在让我们来看看这个公式。首先,若r很大,就只有那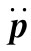 项才重要。B的方向由
项才重要。B的方向由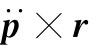 ×r给出,它既垂直于矢径r,也垂直于加速度,如图21-4所示。一切都表明不错,那也是我们由式(21.1′)所得到的结果。
×r给出,它既垂直于矢径r,也垂直于加速度,如图21-4所示。一切都表明不错,那也是我们由式(21.1′)所得到的结果。
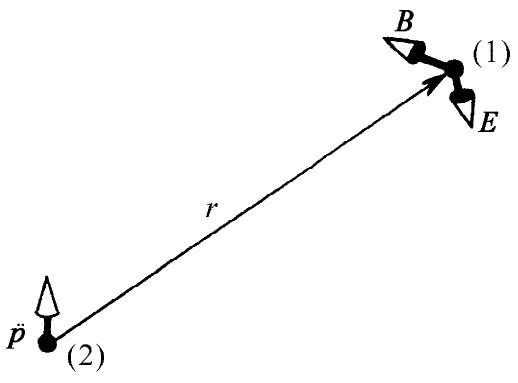
图21-4 一个振荡偶极子的辐射场B和E
现在,让我们来看看以往不熟悉的东西——即在源附近所发生的事情。在§14-7中我们曾求出关于电流元磁场的毕奥-萨伐尔定律。求得一个电流元jdV对于磁场贡献的量为:
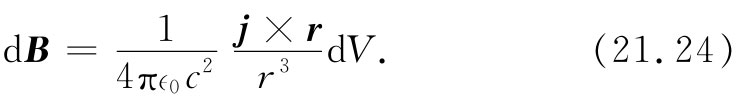
若记得ṗ就是电流,则你知道这个公式看来很像式(21.23)中的第一项。但有一点不同。在式(21.23)中,电流必须在(t-r/c)时刻被算出,而这一点在式(21.24)中就没有出现。然而,事实上,对于小r来说式(21.24)还是十分精确的,因为式(21.23)中的第二 项有助于抵消掉第一项中的推迟效应。当r很小时这两项合起来 给出的结果很接近于式(21.24)。
关于这一点我们可以这样来认识:当r小时,(t-r/c)与t相差无几,因而可以把式(21.23)中的方括号展开成泰勒级数。对于第一项,

而第二项展开至r/c的同一级,则为
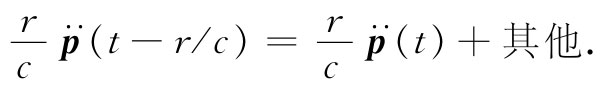
当求和时,含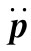 的两项互相抵消,而留给我们是非推迟
电流ṗ也即ṗ(t)——加上(r/c)2
级的项或更高级的项如
的两项互相抵消,而留给我们是非推迟
电流ṗ也即ṗ(t)——加上(r/c)2
级的项或更高级的项如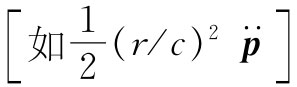 ,对于r足够小以致ṗ在时间r/c内没有显著改变的情况,这些项的贡献将是十分微小的。
,对于r足够小以致ṗ在时间r/c内没有显著改变的情况,这些项的贡献将是十分微小的。
因此,式(21.23)给出的场很像瞬时理论中的场——比带有推迟的瞬时理论要接近得多,推迟的一级效应已被第二项所消除。该静态公式十分准确,其准确程度远比你可能想到的要高。当然,这补偿作用仅对接近源的点才有效。对于远离源的点这个修正变得十分差,因为时间延迟产生了很大的影响,所以我们得到重要的含1/r的辐射项。
仍然存在这样的问题,即算出电场并证明它与式(21.1′)相同。对于大的距离来说我们能够看出该答案将完全正确。我们知道,离源很远、有波传播的地方,E垂直于B(而且也垂直于r),如图21-4所示,并且cB=E。因此,E与加速度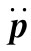 成正比,正如式(21.1′)所料到的那样。
成正比,正如式(21.1′)所料到的那样。
要完全得到在所有距离上的电场,我们需要先解出静电势。当计算A的电流积分以获得式(21.18)时,就曾做过这样一种近似,即把推迟项中r的微小变化忽略不计。这对于静电势来说将行不通,因为这样一来我们获得1/r乘以电荷密度的积分,那将是一个常数。这种近似太粗糙了。我们需要达到一个较高级的近似,但又要避免直接在有关较高级近似的计算中找麻烦,我们还是能够做某一种其他事情的——可以利用已找到的矢势从式(21.6)确定标势。在我们的情况下,A的散度只是∂Az /∂z——因为Ax 和Ay 都恒等于零。用上面求B的同样办法取微分,

积分常数大概相当于某个叠加上去的静场,那当然是有可能存在的静场。但对于我们所考虑的振荡偶极子来说,却不存在静场。
现在我们能够按照
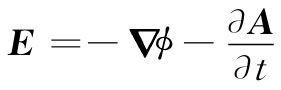
求出电场E。由于计算冗长而不直截了当[只要你记住p(t-r/c)和它对时间的微商之所以与x,y,z有关,是通过推迟时间r/c来的],所以我们将仅仅给出结果:
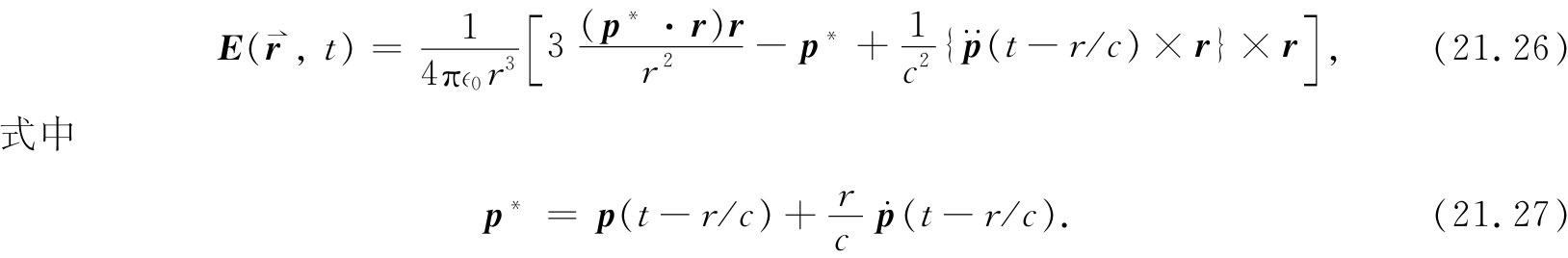
尽管看来它相当复杂,但这个结果还是容易解释的。矢量p*
就是已经被推迟、然后又对推迟“修正”的偶极矩,因而带有p*
的两项就恰恰给出当r很小时的静态偶极子场[见第6章式(6.14)]。当r大时,含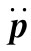 的项占了优势,而电场正比于电荷的加速度,且垂直于r,事实上即是指向
的项占了优势,而电场正比于电荷的加速度,且垂直于r,事实上即是指向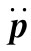 在垂直于r的平面上的投影。
在垂直于r的平面上的投影。
这一结果与我们应用式(21.1)所能得到的结果相符。当然,式(21.1)会更加普遍,它适用于任何运动,而式(21.26)则仅仅适用于推迟时间r/c对于整个源都可以认为是一常数的那种小的运动。无论如何,我们现在已提供了整个以前有关光学讨论的基础(除了某些在第1卷第36章中曾经讨论过的内容以外),因为这种讨论全都与式(21.26)中的末项有关。接下来我们将讨论如何才能得到迅速运动的电荷的场(引导至第1卷第34章中的相对论性效应)。