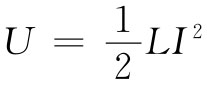 必须由外电路供应;当电流下降到零时,这能量又交还给外电路。在一个理想电感中并没有能量损耗机制。当有一交变电流通过一电感时,能量在它与电路的其他部分之间来回流动,递交给电路的能量的平均
速率为零。这样,我们便说电感是一个无耗
元件,在其中没有电能被消耗掉——也就是“损失”掉。
必须由外电路供应;当电流下降到零时,这能量又交还给外电路。在一个理想电感中并没有能量损耗机制。当有一交变电流通过一电感时,能量在它与电路的其他部分之间来回流动,递交给电路的能量的平均
速率为零。这样,我们便说电感是一个无耗
元件,在其中没有电能被消耗掉——也就是“损失”掉。我们已经看到,要在一个电感中建立起电流I,能量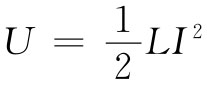 必须由外电路供应;当电流下降到零时,这能量又交还给外电路。在一个理想电感中并没有能量损耗机制。当有一交变电流通过一电感时,能量在它与电路的其他部分之间来回流动,递交给电路的能量的平均
速率为零。这样,我们便说电感是一个无耗
元件,在其中没有电能被消耗掉——也就是“损失”掉。
必须由外电路供应;当电流下降到零时,这能量又交还给外电路。在一个理想电感中并没有能量损耗机制。当有一交变电流通过一电感时,能量在它与电路的其他部分之间来回流动,递交给电路的能量的平均
速率为零。这样,我们便说电感是一个无耗
元件,在其中没有电能被消耗掉——也就是“损失”掉。
同样,一个电容器的能量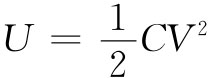 ,当电容器放电时,会归还给外电路。当一电容器置于交流电路中时,能量在其中流进流出,但每一周期中的净能流为零。一个理想电容器也是一个无耗元件。
,当电容器放电时,会归还给外电路。当一电容器置于交流电路中时,能量在其中流进流出,但每一周期中的净能流为零。一个理想电容器也是一个无耗元件。
我们知道,电动势是一个能源。当电流I沿电动势的方向流动时,能量以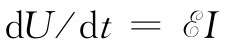 的速率释放给外电路。如果电流是被电路中的其他发电机驱使——逆着
电动势的方向流动,则这电动势将以速率
的速率释放给外电路。如果电流是被电路中的其他发电机驱使——逆着
电动势的方向流动,则这电动势将以速率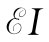 吸收能量;由于I是负的,所以dU/dt也将是负的。
吸收能量;由于I是负的,所以dU/dt也将是负的。
如果一部发电机与一个电阻R相接,则通过该电阻的电流为 。由发电机以速率
。由发电机以速率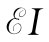 供应的能量为该电阻所吸收。这一能量在电阻中变成热,从而使该电路的电能损失掉。这样,我们便说电能在电阻中耗散
了。在电阻中能量被耗散的速率为dU/dt=RI2
。
供应的能量为该电阻所吸收。这一能量在电阻中变成热,从而使该电路的电能损失掉。这样,我们便说电能在电阻中耗散
了。在电阻中能量被耗散的速率为dU/dt=RI2
。
在交流电路中,能量消耗于电阻中的平均速率等于RI2
在一周中的平均值。由于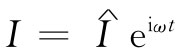 ——这我们实际指的是I正比于cosωt——所以在一周中I2
的平均值就是
——这我们实际指的是I正比于cosωt——所以在一周中I2
的平均值就是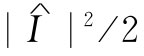 ,因为电流峰值为
,因为电流峰值为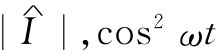 的平均值为1/2。
的平均值为1/2。
当一部发电机接至任意一个阻抗z时,能量的损失又将如何呢(当然,所谓“损失”,我们指的是电能转变为热能)?任何阻抗z都可以写成它的实部及虚部之和。这就是说,
z=R+iX, (22.24)
式中R和X都是实数。从等效电路的观点出发,我们可以讲,任何阻抗相当于一个电阻与一个纯虚数阻抗——称为电抗 ——相串联,如图22-17所示。
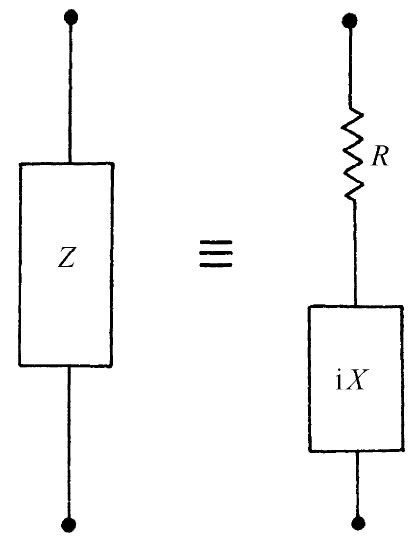
图22-17 任何阻抗都与纯电阻及纯电抗的串联组合等效
我们以前就知道,任何仅由一些L和C组成的电路都具有纯虚数的阻抗。由于平均来讲没有任何能量会在某一个L和C中损失,因而仅含有一些L和C的纯电抗将不会有能量损失。我们可以看到,在一般情况下对于电抗来说这必定是正确的。
如果一部具有电动势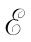 的发电机被连接至图22-17的那个阻抗z上,则来自该发电机的电动势和电流便应有这样一个关系:
的发电机被连接至图22-17的那个阻抗z上,则来自该发电机的电动势和电流便应有这样一个关系:
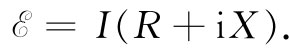 (22.25)
(22.25)
要找出能量输出的平均速率,就要求出乘积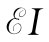 的平均值。此刻我们必须小心!当处理这种乘积时,应与实数值
的平均值。此刻我们必须小心!当处理这种乘积时,应与实数值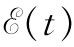 和I(t)打交道(只有当我们具有线性
方程时,复变数函数的实部才会代表实际的物理量;现在我们所关心的是一个乘积
,它肯定就不是线性的)。
和I(t)打交道(只有当我们具有线性
方程时,复变数函数的实部才会代表实际的物理量;现在我们所关心的是一个乘积
,它肯定就不是线性的)。
假定我们选取t的原点以便使振幅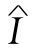 是一实数,比如I0
,那么I的实际时间变化就由下式给出:
是一实数,比如I0
,那么I的实际时间变化就由下式给出:
I=I0 cosωt.
式(22.25)的电动势是下式
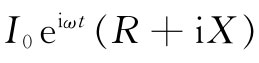
的实部,也即

式(22.26)中的两项分别代表跨越图22-17中R和X的电压降。我们看到,那跨越电阻的电压降与电流同相 ,而那跨越纯电抗部分的电压降则与电流异相 。
由发电机供应的能量消耗的平均速率
〈P〉平均
,等于乘积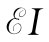 在一周内的积分除以周期T,换句话说,
在一周内的积分除以周期T,换句话说,
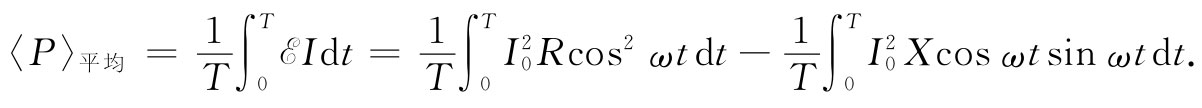
第一个积分为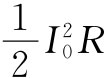 ,而第二个积分为零。所以在一个阻抗z=R+iX中的平均能量损失只取决于z的实部,并且等于
,而第二个积分为零。所以在一个阻抗z=R+iX中的平均能量损失只取决于z的实部,并且等于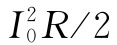 。这同我们以往关于在电阻中的能量损失结果相符,而在电抗部分并没有能量损失。
。这同我们以往关于在电阻中的能量损失结果相符,而在电抗部分并没有能量损失。