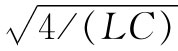§22-7　滤波器

在上一节中，我们看到图22-20中的无限梯形网络会不断地吸收能量，如果它被低于某个临界频率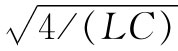 的源所驱动，这个频率将被称为截止频率 ω0 。我们曾经建议，这一效应可以用能量不断沿线向下传输来理解。另一方面，在高频时，即对于ω＞ω0 ，便没有这种能量的连续吸收，这时我们应该期待，电流或许不会沿线向下“透入”得很远。让我们来看看这些想法是否对头。

假设已把该梯形网络的起始端连接到某个交流发电机，试问：梯形网络第754节处电压的情况如何？由于该网络无限长，因而从一节至次一节电压所发生的任何变化总是一样，所以就让我们只来看看当从某节、比如说第n节至下一节所发生的情况。我们将像图22-21（a）所示的那样对电流In 和电压Vn 下定义。

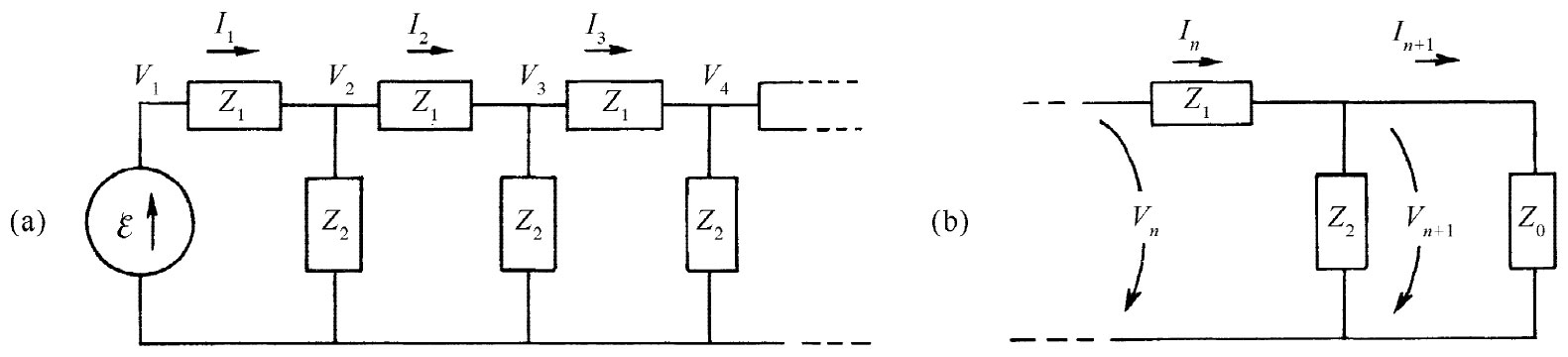
图22-21　找出梯形网络的传播因子

记住在第n节之后，我们总能用特性阻抗z0 来代替该梯形网络的其余部分，这样就可以从Vn 得到Vn+1 ，于是只需对图22-21（b）中的那个电路进行分析。首先，我们注意到，由于Vn 是横跨z0 的电压，因而它必须等于In z0 ，并且Vn 与Vn+1 之差恰好是In z1 ：

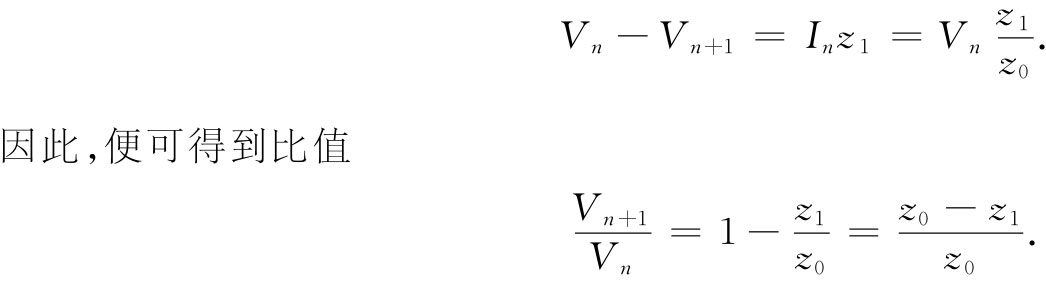
这个比值叫作梯形网络每节的传播因子 ，我们将记为α。当然，这对于所有的节都是相同的：

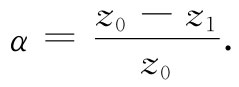　（22.29）

这样，在第n节之后的电压就是

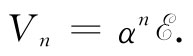　（22.30）

现在你可以找出在第754节之后的电压，它刚好就是α的754次幂乘以 。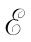

我们看看图22-20（a）中LC梯形网络的α大概是什么。利用式（22.27）的z0 以及z1 =iωL，我们得

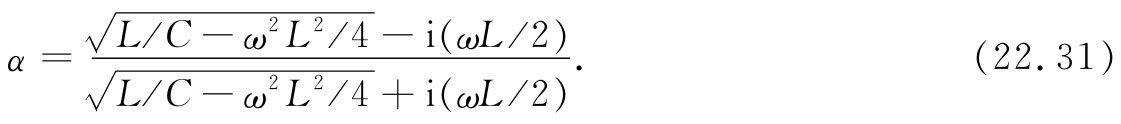
如果驱动频率低于截止频率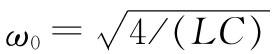 ，则平方根是一实数，而在分子及分母中两个复数的大小值便相等，因此，|α|的量值为1，我们便可写成

α=eiδ ，

这意味着在每节的电压大小都相同，只是相位有变化。事实上，这相位的改变δ是一负数，并代表当沿网络从一节至下一节时电压的“延迟”。

对于比截止频率ω0 高的频率，最好是把式（22.31）的分子和分母中的i消去而重新写成

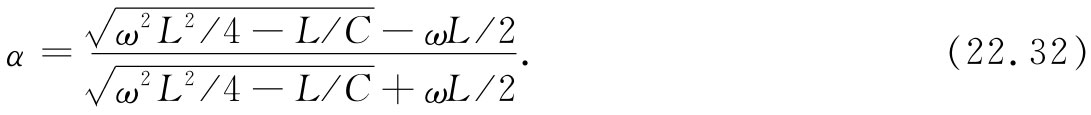
现在该传播因子α是一实 数，而且是一个小于1 的数目。这意味着在任一节上的电压比起其前一节上的电压总要小一个因子α。对于任一比ω0 高的频率，当我们沿该网络下行时，电压降落得很快。α的绝对值作为频率函数而画成的图看来就像图22-22中的那条曲线。

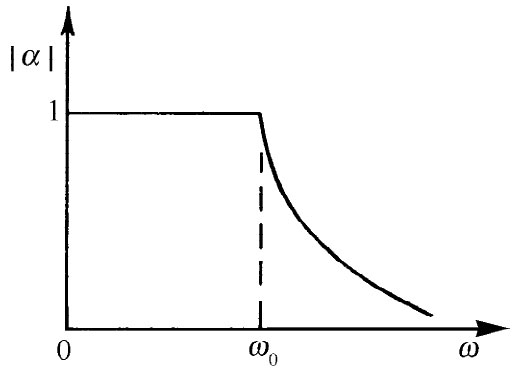
图22-22　在LC梯形网络中每节的传播因子

我们看到，对高于和低于ω0 的频率，α的行为都与我们的这种解释相一致，即对于ω＜ω0 ，该网络会传播能量；而对于ω＞ω0 ，则能量被阻塞。我们说，这网络会“通过”低频而“舍弃”或“滤去”高频。任何一个其特性被设计成按某一规定方式随频率变化的网络都称为“滤波器”。我们刚才分析了一个“低通滤波器”。

你可能会觉得奇怪，为什么要讨论一个显然不能够实现的无限长网络。重要的是，同样的特性可以在一个有限网络中找到，只要我们用一个等于该特性阻抗z0 的阻抗接在其末端使它结束。虽然在实际上是不能够用几个像R，L和C那样的简单元件来严格地 复制出该特性阻抗，但对于某个范围内的频率却往往能够以相当好的近似程度做到这一点。这样，就可以做成性质十分接近于一个无限长网络的一个有限长滤波器。例如，若用一纯电阻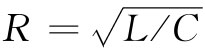 来结束那个LC梯形网络，则它的表现就像上面对它所描述的那样。

如果在那个LC梯形网络中交换各个L和C的位置，以形成如图22-23（a）所示的那种梯形网络，就成为一种传播高 频而抑制低 频的滤波器。通过利用已有的结果，很容易看出在这一网络中发生的事情。你将会注意到，无论什么时候当把L变成C或倒过来 时，也就由每一个iω变成1/iω。因此，过去在ω上所发生的事情现在在1/ω上发生了。特别是，可以通过利用图22-22并将其在横轴上的标记改成1/ω，就像图22-23（b）所表示的那样，我们可以看出α如何随频率而变化。

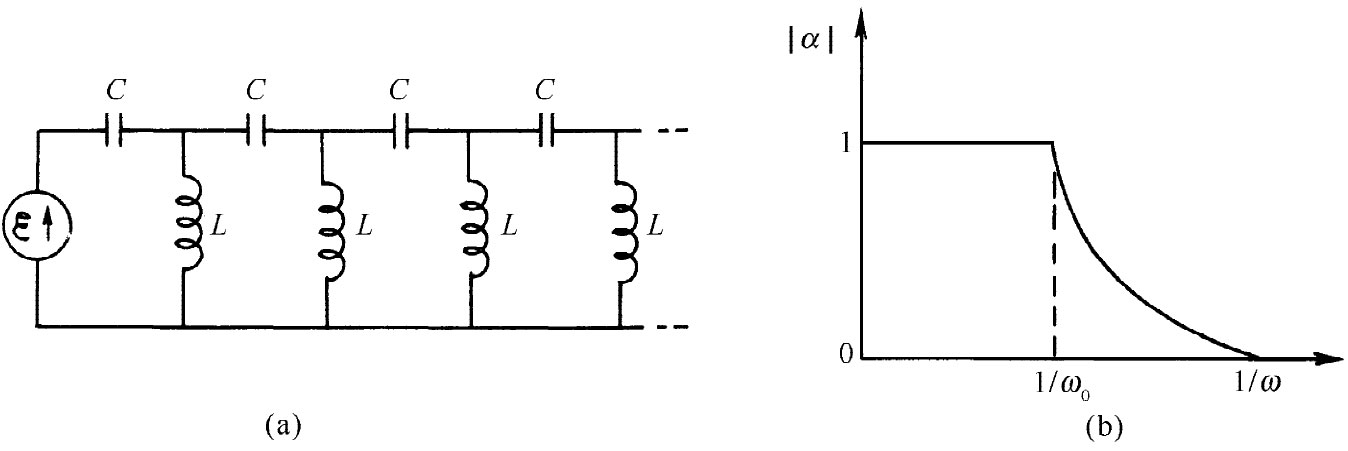
图22-23　（a）高通滤波器；（b）它的传播因子作为1/ω的函数

刚才所描述的低通和高通滤波器具有各种技术应用。LC型低通滤波器常在直流动力供应单元中用作“平流”滤波器。如果要把一个交流电源制造成直流电源，那么先要用一个只允许电流单向流动的整流器。从整流器将会得到看来像图22-24所示的函数V（t）那样的一系列脉冲，那是一种糟糕的直流，因为它上下摆动。假定想要一个漂亮的纯粹直流，像一个电池组所供应的那样，通过在整流器与负载之间放置一个低通滤波器，我们可以接近这一目标。

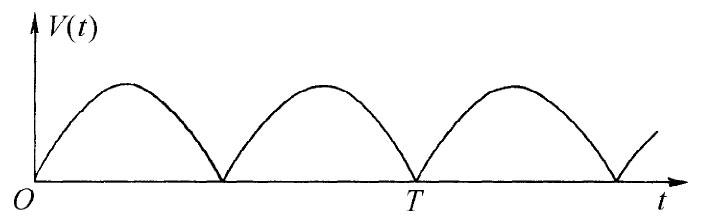
图22-24　一个全波整流器的输出电压

从第1卷第50章中我们知道，图22-24的那个时间函数可以表示为一个恒定电压加上一个正弦波、再加上一系列更高频率的正弦波的叠加——即由一个傅里叶级数来表示。如果滤波器是线性的（正如我们曾经假定的，只要那些L和C都不随电流或电压而变），那么从滤波器出来的就是对输入端每一成分的各项输出的叠加。如果安排得使滤波器的截止频率ω0 远低于函数V（t）中的最低频率，则直流（ω=0）便能够很好地通过，但第一谐波的振幅将被削弱得很厉害，而那些更高谐波的振幅被削弱得更多。所以我们能够获得一个想要的平滑输出，它只决定我们乐意购买多少节滤波器。

如果希望抑制某些低频波，则常用高通滤波器。例如，在一留声机的放大器中，高通滤波器可以用来让音乐通过，而避开那些来自转盘电动机的低调隆隆声。

也可能制成一种“带通”滤波器，它会抑制比某一频率ω1 低而比另一频率ω2 （大于ω1 ）高的一些频率，而却让ω1 与ω2 之间的那些频率通过。这可很容易地把一个高通与一个低通滤波器放在一起而做到，但更经常的却是通过制造一个梯形网络来实现的。在该网络中，其阻抗z1 和z2 更加复杂——每一个都是若干个L和C的组合。这样一个带通滤波器也许具有如图22-25（a）所示的那种传播常数。这可能用来把一些仅占据一个频率间隔的信号——诸如在一高频电话电缆中的许多声音信道的每一个，或在无线电传递中受了调制的每一个载波——分开来。

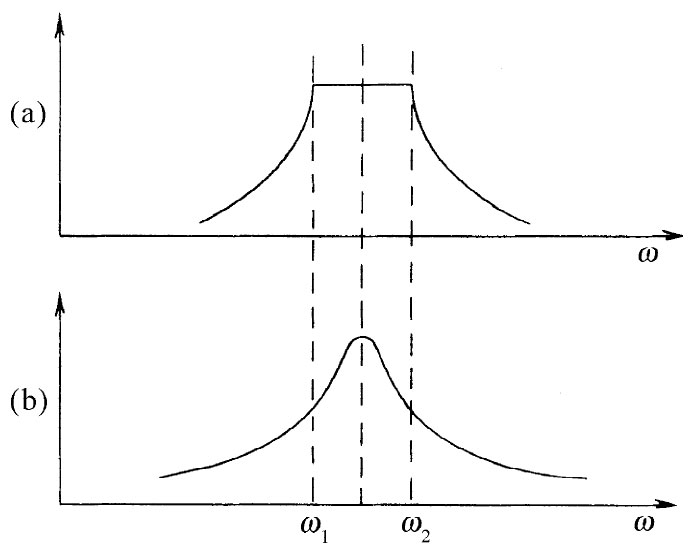
图22-25　（a）带通滤波器；（b）简单的共振滤波器

在第1卷第25章中我们曾经见到，像这样的滤波作用也可利用一普通共振曲线的选择性来做到，为了比较，我们已把该共振曲线画在图22-25（b）上。但对于某些目的来说，这一种共振式滤波器不如带通滤波器那么优越。你会记得（第1卷第48章），当频率为ωc 的载波受到“信号”频率ωs 所调制时，整个讯号不仅含有载频，而且还含有两个边带频率ωc +ωs 和ωc -ωs 。采用共振式滤波器时，这些边带总多少会受到衰减，而且信号的频率越高则衰减越厉害，正如你可以从图上见到的。因此存在不良的“频率响应”，那些较高频的乐音通不过去。但若滤波作用是由一个设计得使宽度ω2 -ω1 至少两倍于最高信号频率的那种带通滤波器来完成的话，则该频率响应对于所需的那些信号来说就将是“平坦”的了。

关于梯式滤波器我们还要再强调一点：图22-20的LC梯形网络也是传输线的一个近似表示。如果有一长导体与另一导体平行并列——诸如在一根同轴电缆中的导线或一根悬挂在地面之上的导线——那么便会有某些电容存在于两导体之间，以及由于它们之间存在磁场所以还有某些电感。若我们设想该传输线被分割成众多小段Δl，每一段看起来就像在LC梯形网络中由串联电感ΔL和并联电容ΔC所构成的一节。然后，我们便能应用有关梯式滤波器的结果。若取Δl趋于零时的极限，则对于传输线就有一个极好描述。注意当Δl变得越来越小时，ΔL和ΔC两者都会减少，但都在同一比例上，因而比值ΔL/ΔC仍将保持不变。因此，若取ΔL和ΔC都趋于零时式（22.28）的极限，则我们发现该特性阻抗是一个大小为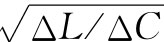 的纯电阻。我们也可将比值ΔL/ΔC写成L0 /C0 ，其中L0 和C0 分别代表传输线每单位长度的电感和电容，于是我们得

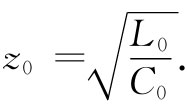　（22.33）

你也将会注意到，当ΔL和ΔC各趋于零时，截止频率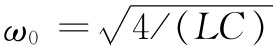 会变成无限大，即对于一条理想的传输线来说不存在截止频率。