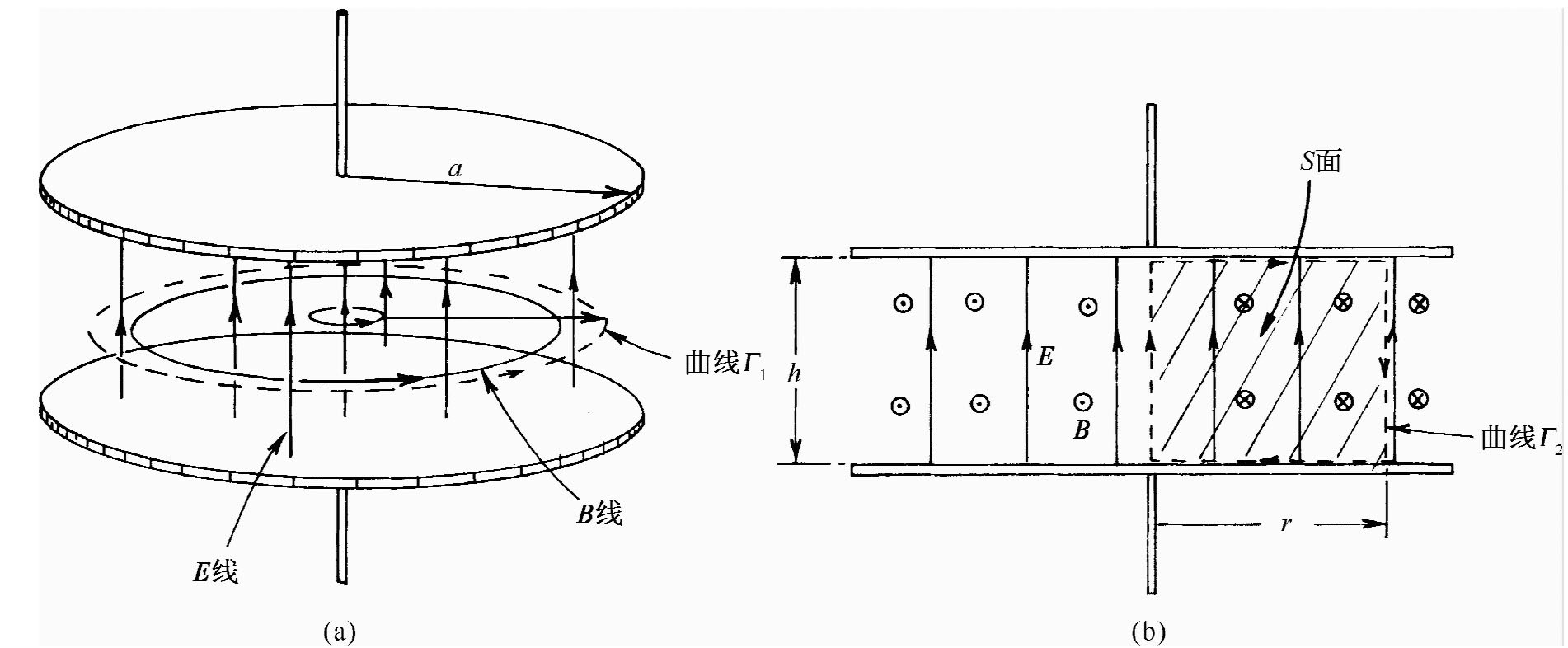
图23-4 电容器两极板间的电场和磁场
现在我们要来详细讨论当频率变得越来越大时一个电容器——几何上的理想电容器——的行为，使我们能够看到其性质的转变（我们宁可采用电容而不采用电感，为的是一对板的几何形状比一个线圈的几何形状要简单得多）。我们考虑图23-4（a）所示的那个电容器，构成它的两块平行圆板用一对导线接至外界发电机上。如果用直流对电容器充电，则在其中一板上将有正电荷，在另一板上有负电荷，而在两板之间则有一匀强电场。
图23-4 电容器两极板间的电场和磁场
现在假定不用直流，而是加一个低频交流电于两板上（往后我们将会知道什么是“低”频，什么是“高”频）。比方说，把电容器连接至一低频发电机上。当电压正在交变时，上板的正电荷会被取出而换上了负电荷。在这一事情发生时，电场会随之消失，然后又在相反的方向上建立起来。当电荷缓慢地来回涌动时，电场也跟着变化。除了一些我们将要加以忽略的边缘效应外，在每一瞬间电场是均匀的，如图23-4（b）所示。可以把电场的大小写成
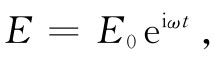（23.2）
式中E0 是一常数。
现在，当频率升高时，这是否仍然正确呢？不，因为当电场增高和降低时就会有电通量穿过像图23-4（a）中的任意回路Γ1 。而正如你所知的，一个变化的电场会起到产生磁场的作用。麦克斯韦方程组中一个方程讲，当有变化的电场时，犹如这眼前存在的那样，就一定有磁场的线积分。环绕某一闭合环的磁场积分乘以c2 之后，就等于穿过该环内面积的电通量的时间变化率（如果没有电流的话）：
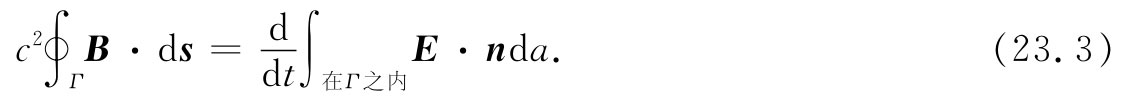
所以，到底磁场有多大呢？计算并不十分困难。假定考虑回路Γ1 ，它是一个半径为r的圆周。我们能够从对称性看出，磁场会环绕图中所示的那种圆周转。这样B的线积分就是2πrB。而且由于电场是均匀的，所以电场通量简单地等于E乘以该圆周的面积πr2 ：
对于交变场来说，E对时间的微商仅是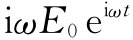
。因此我们求得，该电容器具有磁场
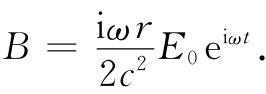（23.5）
换句话说，磁场也在振动，而且具有正比于半径r的强度。
这种情况会产生什么影响呢？当有一个正在变化的磁场时，便将产生一些感生电场，而该电容器将开始有点像一个电感的作用了。当频率升高时，这磁场变得较强，它与E的变化率成正比，因而也与ω成正比。该电容器的阻抗将不再简单地等于1/（iωC）。
让我们继续提高频率，并更仔细地分析将会发生的情况。我们有一个来回涌动的磁场。但这时的电场就不可能像我们所曾假定的那样是均匀的了！当有一正在变化的磁场时，就必然有一个电场的线积分——根据法拉第定律。所以，如果有一个相当大的磁场，正如在高频时就开始发生的那样，则电场不可能在离开中心的所有距离处都相同。电场必须随r改变，才能使电场的线积分等于变化着的磁场通量。
让我们来看看能否算出正确的电场。通过算出我们原来对低频时假定的匀强场的“修正”，便能够完成此事。现在把该匀强场称作E1
，它仍旧是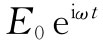
，而把正确的场写成
E=E1 +E2 ，
其中E2
就是由于变化着的磁场所引起的修正。对于任意频率ω，我们将把在该电容器中心处的场写成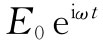
（因而定义了E0
），使得在这中心处并不需要修正，即在r=0处E2
=0。
为求得E2 可利用法拉第定律的积分形式：
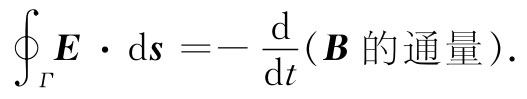
这些积分很简单，只要取积分回路像图23-4（b）所示的曲线Γ2 那样，即沿轴上升，当达到上板时再沿半径向外伸展至距离r处、又垂直地落到底板、然后又返回到轴上。E1 环绕这个曲线的线积分当然是零，所以就只有E2 做出贡献，而它的积分正好是-E2 （r）·h，其中h是两板间的距离（如果E指向上我们称为正）。这等于B通量的变化率，我们得通过对图23-4（b）中Γ2 之内阴影面积的积分来获得。穿过宽度为dr的垂直狭条的通量为B（r）hdr，因而总通量就是
h∫B（r）dr.
令这一通量的-∂/∂t等于E2 的线积分，便有
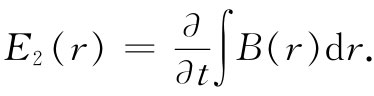（23.6）
注意式中h已消去了，场与两板间的间距无关。
利用关于B（r）的方程式（23.5），我们便有
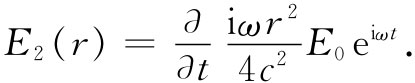
对于时间的微商只不过带来另一个因子iω，这样我们得
正如所预期的，这感生电场倾向于把远离中心的电场减弱 。于是，改正后的场E=E1 +E2 为
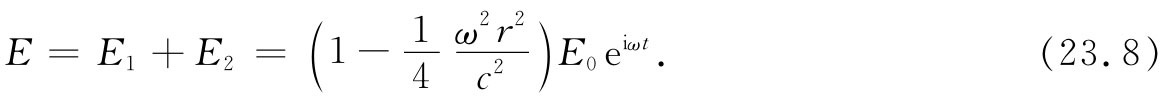
在电容器中的电场不再是均匀的，它具有如图23-5中虚线所示的那种抛物线形状。你看，我们的简单电容器已变得稍微复杂些了。
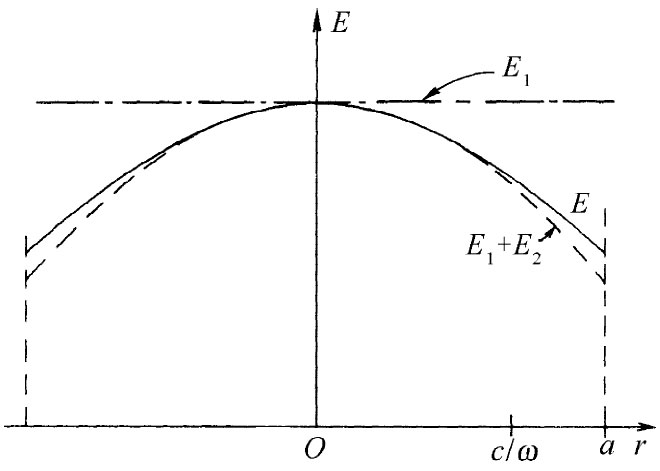
图23-5 在高频时电容器两板间的电场（边缘效应已被忽略）
现在有可能利用所得结果来计算电容器在高频时的阻抗。知道了电场后，理应能够算出板上的电荷并求出通过电容器的电流如何依赖于频率ω，但目前我们对这个问题不感兴趣。更感兴趣的是要看看当继续提高频率时会发生什么情况——看看在更高频率上所发生的事情。我们的工作是否结束了呢？不，因为已修正了电场，这就意味着已算出来的磁场不再是正确的了。式（23.5）中的磁场也是近似正确的，但它仅是一级近似，所以就让我们叫它作B1 。这样应将式（23.5）重新写成
你会记得，这个场是由E1 的变化产生的。现在正确的磁场将是由总电场E1 +E2 所产生的。若把磁场写成B=B1 +B2 ，则其中第二项就恰好是由E2 所产生的附加场。为求出B2 ，可以通过我们求B1 时用过的相同论证来进行，B2 环绕曲线Γ1 的线积分等于E2 穿过Γ1 的通量的变化率。我们将仍然有式（23.4），其中用B2 代替B而用E2 代替E：
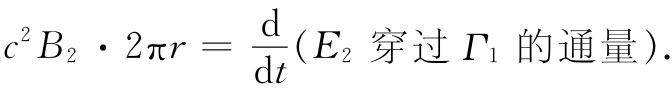
由于E2 随着半径变化，因而要获得它的通量就得对Γ1 内的圆面积进行积分。用2πrdr作为面积元，这个积分就是
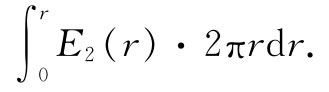
因此对于B2 （r）我们得到
利用来自式（23.7）的E2 （r），我们需要对r3dr进行积分，而这当然为r4 /4。对于磁场的修正变成
可是事情还没有完成！如果磁场并不与我们最初所设想的相同，则刚才对E2 的计算便不能认为是正确的。我们必须对E进一步做出修正，它由额外磁场B2 产生。让我们把这个对电场的附加修正叫作E3 。它与磁场B2 的关系犹如E2 与B1 的关系一样。我们可以再一次利用式（23.6），只不过改变其中的下脚标：
利用上面关于B2 的结果，即式（23.11），对电场新的修正为
把经过了两次修正的电场写成E=E1 +E2 +E3 ，我们得
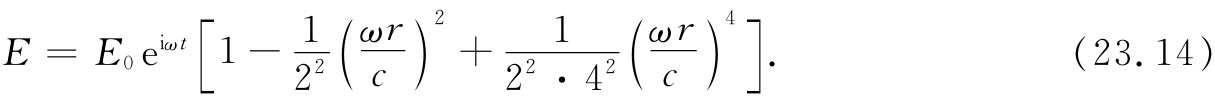
电场随r的变化不再是我们曾在图23-5中画出来的那条简单抛物线，而是在较大的半径处略高于（E1 +E2 ）曲线。
事情还未最后完成。新的电场对磁场产生一个新的修正，而这个被重新修正了的磁场又将对电场产生一个进一步的修正，如此等等。然而，我们已经有了所需的全部公式。对于B3 可以利用式（23.10），把其中B和E的下脚标从2改成3。
对电场的下一次改正是
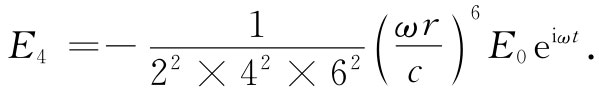
因此，在达到这一级时，整个电场就由下式给出：
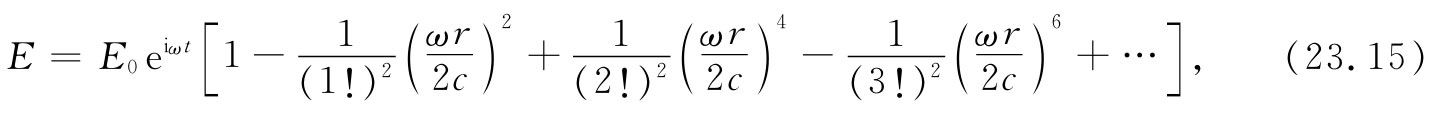
其中我们已把各数字系数写成这样一种形式，以便对该级数应如何继续下去看得更清楚。
我们的最后结果是：在该电容器两板间的电场，对于任一频率来说，都等于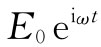
乘以仅含有变量ωr/c的一个无穷级数。如果我们乐意，就可以定义一个特殊函数，这函数将称为J0
（x），作为出现在式（23.15）中方括号内的无穷级数。
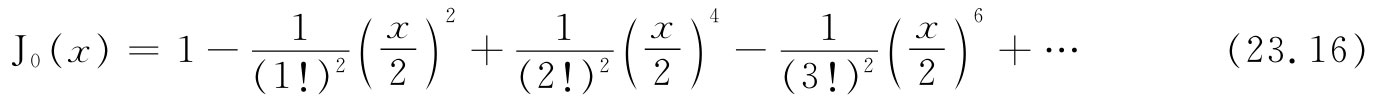
这样，就可以将我们的解写成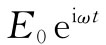
乘以这个函数，其中x=ωr/c：
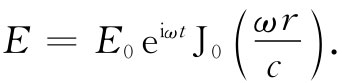（23.17）
之所以叫这个特殊函数为J0 的原因是：自然，这并非是计算柱体中振动这一问题才开
始用的，其实这一函数以前就已出现过而且经常被称为J0 。每当你求解具有柱对称的波动问题时它总是发生。函数J0 对于柱面波就好像余弦函数对于沿直线传播的波一样，因此它是一个重要函数，发现已多时了，以后与一个叫贝塞尔（Bessel）的人的名字联系上了。那个下脚标零意味着贝塞尔曾经发现过整个一系列不同的函数，而这只是其中的第一个。
其他的贝塞尔函数J1 ，J2 等等是处理与强度随着绕圆柱轴的角度而变的那些柱面波所必需的。
在我们的圆形电容器两板间，电场经过完全修正已由式（23.17）给出，它已被画成图23-5中那条实曲线。对于不太高的频率，我们的二级近似就已经很好。三级近似甚至会更好——事实上，好到要是我们把它画出来，你不可能会看出它与那条实线间的差别。然而，你将在下一节中见到，对于大的半径或高的频率，为获得一个准确描述，整个级数就是必需的了。