§23-4　腔模

假设现在我们试图通过对实际盒子做测量来检验上述理论。取一个圆柱形盒子，其直径为3.0in而高度约2.5in。这个盒子装配有如图23-8所示的一个输入和输出回路。若按照式（23.18）算出关于这个盒子预期的共振频率，则可得f0 =ω0 /（2π）=3010MHz。当我们把信号发生器的频率设置在3000MHz左右并稍微变更这一频率以获得共振时，就会观察到最大的输出电流发生于频率为3050MHz处，这数值很接近于那预期的共振频率，但不完全相同。产生这一差异有几种可能原因。或许由于为要放进耦合回路而挖开的那些小洞会使共振频率有了一点变化。然而，稍微想一下就会明白，那些小洞理应使共振频率略有降低，因而这不能成为理由。或许是在校准信号发生器时稍微有一些误差，也许是我们对空腔的直径量得不够准确。但无论如何，还是符合得相当好的。

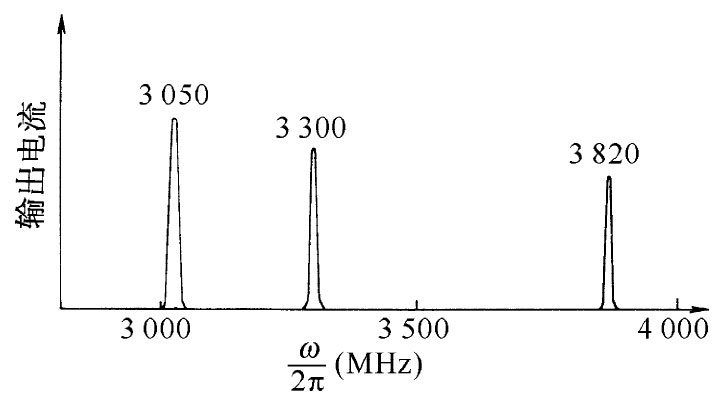
图23-11　对一柱形空腔所观测到的几个共振频率

更为重要的是：当信号发生器的频率在3000MHz以上改变一些时所发生的情况。当我们这样做时，便会获得如图23-11所示的那些结果。我们发现，除了在3000MHz附近那个预期的共振外，还有一个接近于3300MHz和另一个接近于3820MHz的共振。这些附加的共振意味着什么呢？我们也许可从图23-6获得一条线索。尽管曾经假定贝塞尔函数的第一个零点出现在盒子的边缘，但也有可能贝塞尔函数的第二个零点与盒子的边缘相对应，因而当我们从盒子中心移动至边缘时电场恰好完成一个完整的振动，如图23-12所示。这是关于振动场的另一种可能模式。我们应当肯定地预期盒子会以这种模式发生共振。可是要注意，贝塞尔函数的第二个零点发生在x=5.52处，那比起第一个零点处的值不止大一倍。因此，这个模式的共振频率就应比6000MHz还高。无疑，我们会在那里找到它的，但却不能用它来解释在3300时所观测到的那个共振。

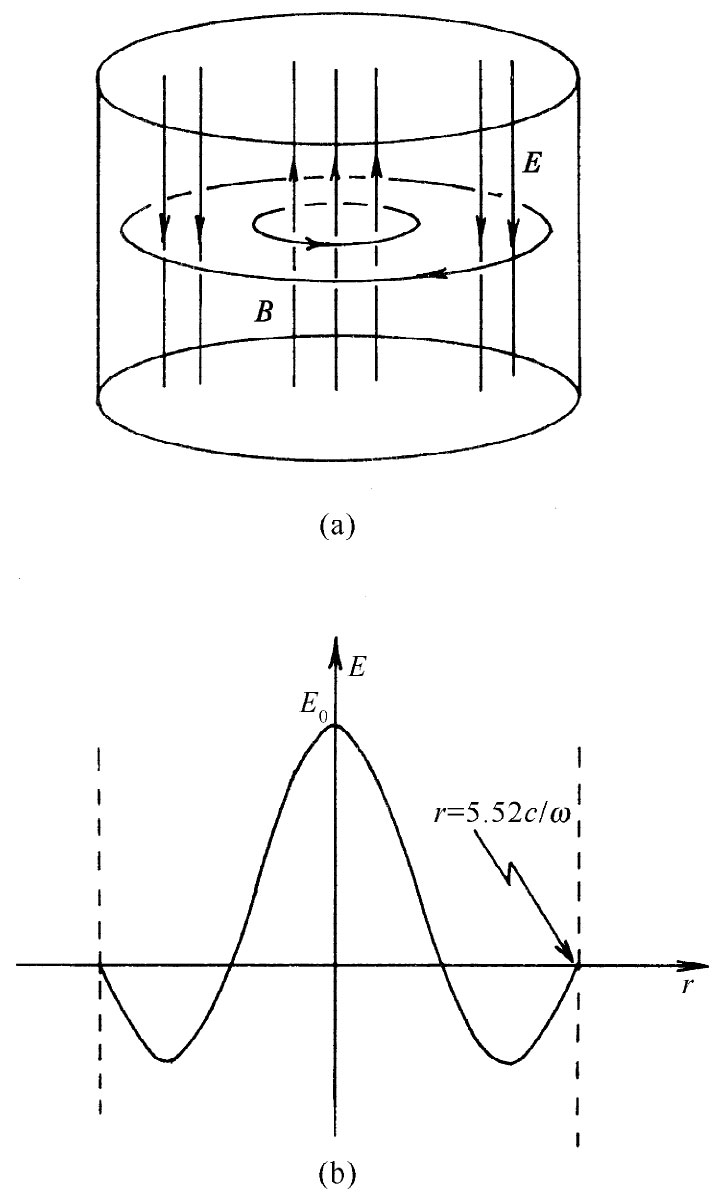
图23-12　更高频率的模式

麻烦就在于对有关共振腔行为的分析，我们只考虑了电场和磁场一种可能的几何布局。已经假定电场是垂直的而磁场则位于一些水平圆周上。但别的场也是有可能的。唯一的要求是，在盒子里的电场和磁场都必须满足麦克斯韦方程组而且电场还必须与盒壁正交。我们已考虑其中盒子顶部和底部都是平坦的那一种情况，但要是顶和底都弯曲，事情也不会完全不同。事实上，盒子怎么能够被认为知道哪是它的顶、底以及侧面呢？实际上能够证明，在盒内就存在电场或多或少穿越直径的那一种振动模，如图23-13所示。

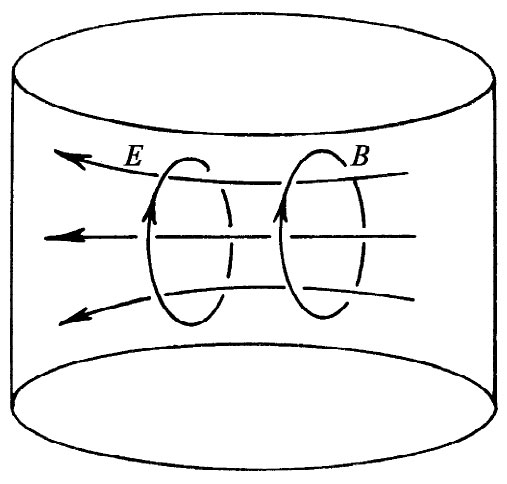
图23-13　柱形空腔的一种横向模

要理解为什么这一模式的固有频率与我们所曾考虑过的第一个模式的固有频率不应有很大差别，并不是太困难的。假设不取该柱形空腔，而是取一个每边3in的立方形空腔。很清楚，这个空腔该有三种不同模式，但都有相同的频率。其中电场几乎是上下振动的一种模式肯定将与其中电场是左右指向的另一种模式具有相同频率。如果我们现在将该立方形空腔扭曲成一圆筒，就会或多或少改变其频率。但仍应该期望，这些频率不会改变得太多，只要对该空腔的尺寸大约保持一样。因此，图23-13那种模式的频率应不太异于图23-8的模式。本来我们可以对图23-13的那种模式详细算出其固有频率，但现在还不打算那样做。当这些计算做出来时，便会发现，对于上面所假定的那些尺寸，算出的共振频率的确很接近于在3300MHz处所观测到的共振的频率。

通过相似的一些计算还能够证明，应该还有另外的模式，其共振频率为我们已找出的接近3800MHz的那个频率。对于这一模式，电场和磁场如图23-14所示。不必担心该电场会自始至终横穿过空腔。它从侧壁跑至两端，如图所示。

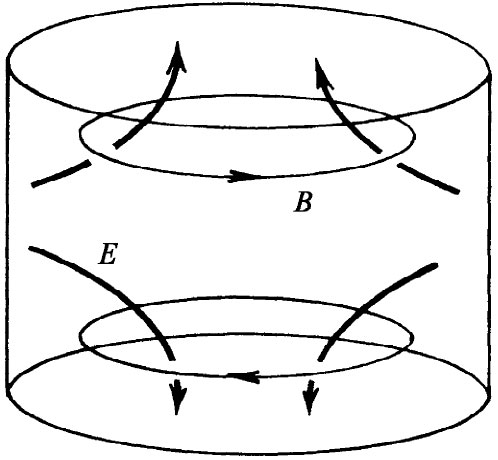
图23-14　柱形空腔的另一种模

那么你现在大概会相信，若把频率增加得越来越高，则应该指望会找到越来越多的共振。存在许多不同的模式，每一个都具有与电场和磁场的某一特定的复杂布局相对应的不同共振频率。这些场的每一种布局称为共振模。通过求解关于空腔里的电场和磁场的麦克斯韦方程组，每一种模式的共振频率就可以计算出来。

当有了在某个特定频率处的共振时，我们怎样才能知道被激发的是哪一模式呢？一种办法是，通过一个小洞把一根小导线插进空腔里。如果电场沿着导线方向，如图23-15（a）所示，则导线里便有一个相对较大的电流从电场汲去能量，因而共振将被抑制。若电场像图23-15（b）所示的那样，则影响会小得多。通过把导线的末端弯曲，像图23-15（c）那样，我们可以找出这种模式中场所指的方向。于是，当把导线转动使其末端与E平行时影响便大，而当转动至与E成90°时影响就小。

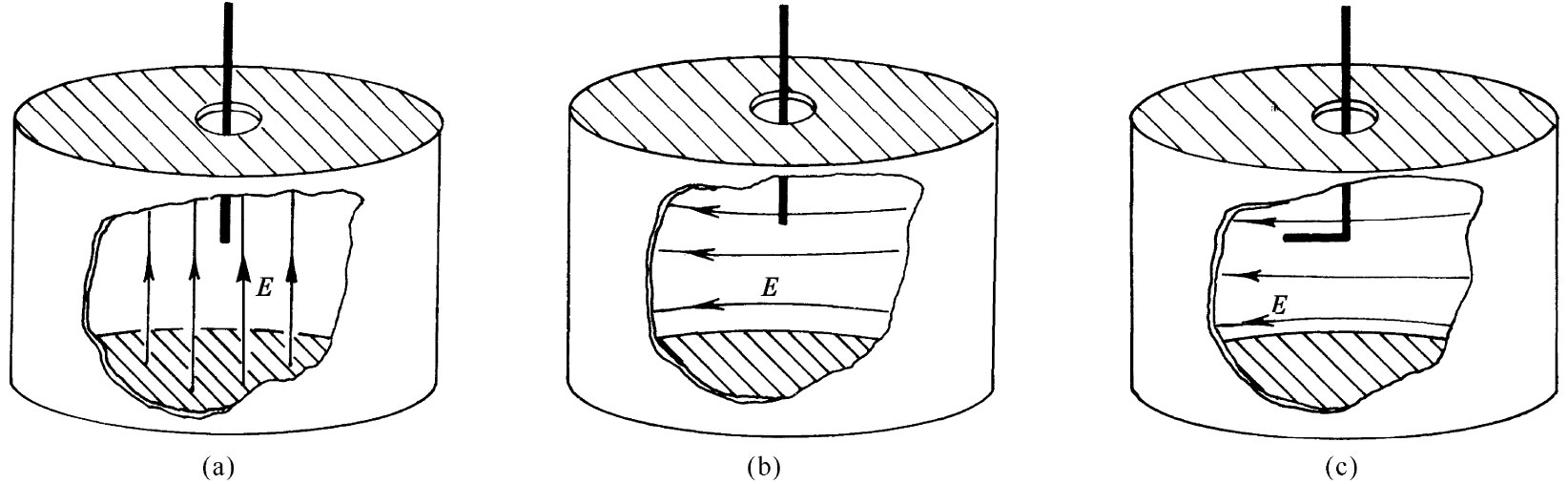
图23-15　一根伸进空腔里的短金属线，当其平行于E时，对共振的干扰比起与E垂直时要大得多