在解方程式（24.16）以求得kz 时，实际应有两个根，一个是正，一个是负。我们应该写成
这两个符号只是意味着可能有以负相速（朝向-z）传播的波，同样在导管中也有沿正向传播的波。自然，波沿任一方向传播都应该是可能的。由于这两种类型的波可以同时存在，所以就会有驻波解的可能性。
有关kz 的方程也告诉我们，较高的频率给出较大的kz 值，因而也就是较短的波长，一直到ω取大的极限时，k变得等于ω/c，它就是我们对自由空间里的波所预期的值。我们通过管子所“看到”的光仍然以速率c行进。但此刻注意，若频率下降，则某些怪事会跟着发生。开始波长会变得越来越大，但若ω降得太小，则式（24.20）中的平方根内的量突然变负。一旦ω变为小于πc/a——或当λ0变得大于2a，上述情况就会发生。换句话说，当频率变成低于某一临界频率ωc =πc/a时，波数kg （从而λg ）会变成虚数，从而不再得到任何解了。难道真的得不到解了吗？谁说kz 必须是实数呢？如果确实出现虚数，那又该怎么办呢？场方程组仍旧被满足，或许一个虚数kz 也代表一个波。
假设ω小于ωc ，便可以写成
kz =±ik′， （24.21）
其中k′是正的实数，即
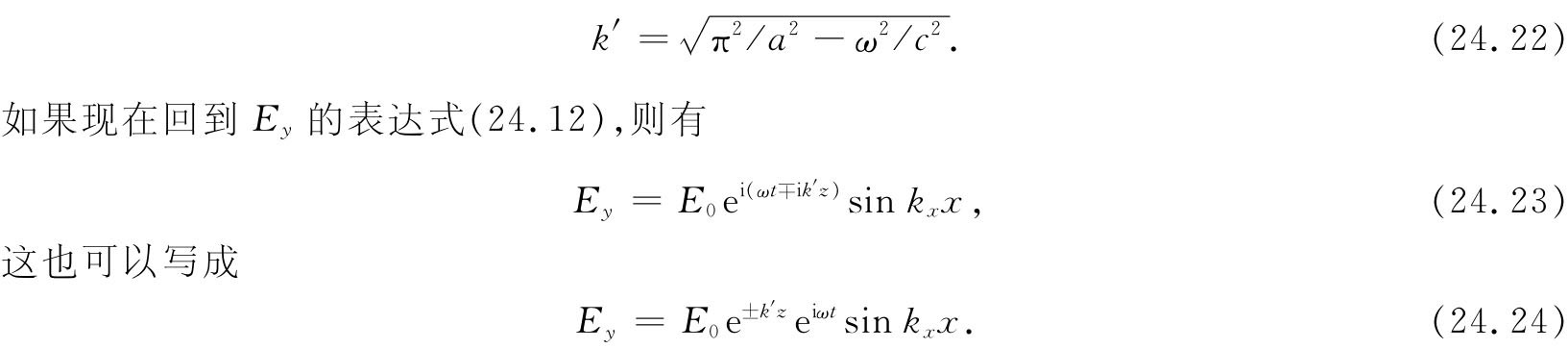
上述表达式给出了一个按eiωt
随时间振动但却按照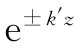
随z变化的E场。它作为一个指数函数随z平滑地减少或增加。在我们的推导中并未对发出波的源有所操心，不过一定有一个源存在于导管中某处。伴随k′的符号必定是使场随着离开波源的距离增大而减小的那个。
因此，对于比ωc =πc/a低的频率，波并不会 沿导管往下传播，该振动场只能透入导管内仅达到1/k′数量级的距离。为此，频率ω0 被称作导管的“截止频率”。考察式（24.22）可知，在频率仅稍低于ωc 时，k′是一个小数值，因而场可透入导管内很大的距离。但若ω比ωc 小很多，则指数系数k′等于π/a，而场便非常迅速地减弱，如图24-7所示。在距离等于a/π或在约三分之一宽度的距离内，场减弱至1/e。场从源出来后仅透入很短距离。
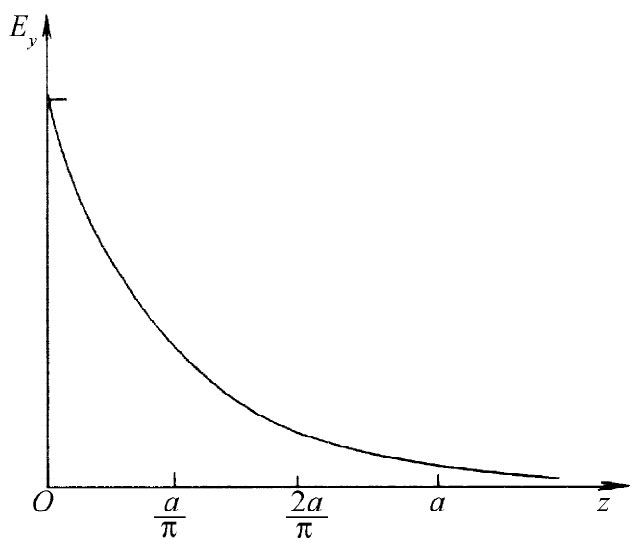
图24-7 对于ω≪ωc ，Ey 随z的变化情况
我们想要强调对导波进行分析的一个有趣特点——即虚波数kz 的出现。按正常情况，如果在物理学中求解一个方程并获得一个虚数，它不具有任何物理意义。然而，对于波 来说，一个虚数确实 意味着某种东西。波动方程仍被满足，它只是意味着解答会给出一个指数式地减弱的场，而不是一个传播着的波罢了。因此，在任一个波动问题中，若对于某一频率k会变成虚数，这意味着波的形式变了——正弦波变成了指数式衰减的场。