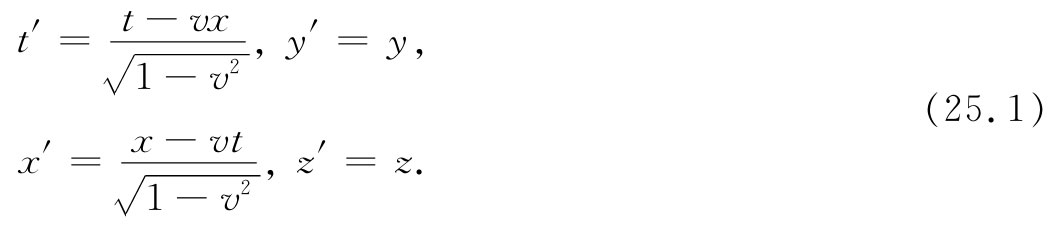
现在来讨论狭义相对论在电动力学中的应用。由于已在第1卷的15至17章中学习过狭义相对论,因而我们在此只要很快地温习一下基本概念。
在实验上已经发现:如果我们以匀速运动,则物理规律不会改变。你不可能区别你是否处于一艘以匀速沿直线航行的宇宙飞船中,除非你从飞船中向外观望,或至少得做一种与外界有关的观测。我们写出的任何正确的物理定律都必须安排得使自然界的这一事实成为其中的固有部分。
设存在两个坐标系,其中一个S′系在x方向上以速率v相对于另一个S系而做匀速运动,这两个坐标系的空间与时间之间的关系由洛伦兹变换式 给出:
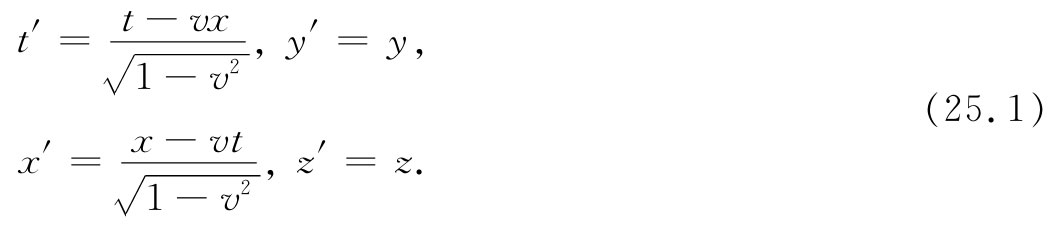
物理定律必须是这样的:在经过了洛伦兹变换之后,该定律的新形式看来刚好像其旧形式。这恰恰同物理定律与坐标系的取向 无关的原理相似。在第1卷第11章中,我们已看到,要从数学上描写物理过程对于转动的不变性,其办法是利用矢量 来写出方程式。
例如,若有两矢量
A=(Ax ,Ay ,Az )和B=(Bx ,By ,Bz ),
我们曾发现其组合式
A·B=Ax Bx +Ay By +Az Bz
如果对转动的坐标系进行变换,是不变的。因此我们知道,若在一个方程式的两边都有像A·B这一类的标识,则这方程在所有转动坐标系中都会有完全相同的形式。我们也曾发现过这么一个算符(见第2章):
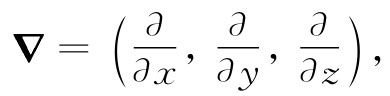
当作用于一标量函数时,它会给出像一个矢量那样变换的三个量。利用这一算符我们曾定义过梯度,而与其他矢量相组合时也曾定义过散度与拉普拉斯算符。最后还发现,取两矢量的各对分量之积并求和,可能得到三个新的量,其行为像一个新的矢量。我们曾称它为两矢量的叉积 。然后,又利用算符▽做叉积,定义了矢量的旋度。
由于我们会经常回过去参考矢量分析中所曾做过的事情,因此就把过去用过的三维空间中所有重要的矢量运算的摘要罗列在表25-1上。这里的要点在于,必须将物理学方程写得能使其两边在坐标系转动时以相同的方式变换。如果一边是矢量,则另一边也必须是矢量,以便在坐标系转动后方程两边将以完全相同的方式一起改变。同理,若一边是标量,则另一边也应该是标量,因而当转动坐标系时两边都不应当有任何改变,等等。
表25-1 三维矢量分析中重要的量和重要运算

现在,在狭义相对论的情况下,时间和空间不可分割地混在一起,因而就必须对四维做出类似的事情。我们希望所得的方程不仅对于转动会保持不变,而且对于任何 惯性参照系也是如此。这意味着,方程式在经历了式(25.1)的洛伦兹变换后应该不变。本章的目的就是要向你们说明如何才能做到这一点。然而,在开始之前,还要做一件将使我们的工作轻松得多(也会减少某些混乱)的事情。这就是选取长度和时间单位使得光速c等于1。你可以把这看作为把时间单位选取为光行走1m所需的时间 (约为3×10-9 s)。我们甚至可以叫这个时间单位为“一米”。采用这种单位,一切方程会更明显地呈现出空时对称性。并且,所有的c将不再出现在我们的相对论方程式中(如果你对此觉得麻烦的话,你始终可用ct代替每一个t,或一般说来,通过在那些需要使方程的量纲表现得正确的地方添加一个c,即把c再放回到任一个方程中去)。有了这个约定,我们就准备开始工作。我们的计划是要在四维空时中做出曾用矢量在三维中所做过的所有事情。这诚然是一场十分简单的游戏,我们只是根据类比来做工作罢了。唯一真正的复杂性是符号的表示方法(在三维时已用尽了矢量符号)以及符号的一个轻微扭曲。
首先,通过与三维中的矢量的类比,定义一个四维矢量 为at ,ax ,ay ,az 一组的四个量,当我们变换运动坐标系时,这些量会像t,x,y,z那样变换。对于四维矢量人们使用几种不同的符号表示方法。人们会写成aμ ,这指的是四个数(at ,ax ,ay ,az )的一组——换句话说,该下脚标μ可以取t,x,y,z各“值”。有时由一个三维矢量来指明它的三个空间分量,即像(at ,a)那样,也会很方便。
我们已碰到过一个四维矢量,它由粒子的能量和动量组成(第1卷第17章),在新符号表示法中我们把它写成
pμ =(E,p), (25.2)
这意味着该四维矢量pμ 是由粒子的能量及其三维矢量p的三个分量所构成的。
看来似乎这场游戏的确十分简单——对于物理学中每一个三维矢量,我们必须做的全部事情就在于找出其余的一个分量该是什么,从而就有一个四维矢量了。为了弄清楚事实并不是那么回事,试考虑速度矢量,它的分量是
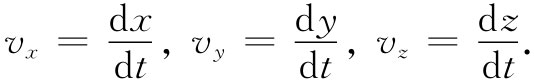
试问:那时间分量是什么?凭本能就应能够提供正确的答案。由于四维矢量都像t,x,y,z那样,我们就会猜测到其时间分量为
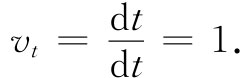
这是错的 。原因是,当我们做洛伦兹变换时在每个分母中的t并非是不变量。虽然为构成一个四维矢量,那些分子都具有正确的行为,但在各个分母中的dt却把事情搞坏了,它并不是对称的,而且在两个不同系统中是不相同的。
事实证明,只要各除以 ,上面所写下的四个“速度”分量将成为四维矢量的分量。我们能够看出那是正确的,因为如果从动量四维矢量出发:
,上面所写下的四个“速度”分量将成为四维矢量的分量。我们能够看出那是正确的,因为如果从动量四维矢量出发:
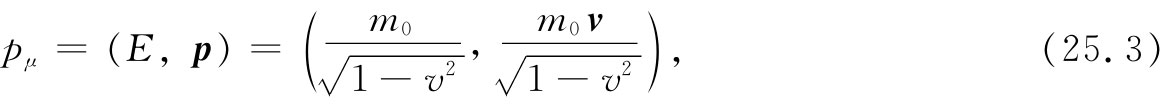
并用四维 中不变的标量、静止质量m0 来除它,便有

这必然仍是一个四维矢量(用一个不变标量 来除,并不会改变变换性质)。因此,就可由下式定义 一个“速度四维矢量 ”uμ :
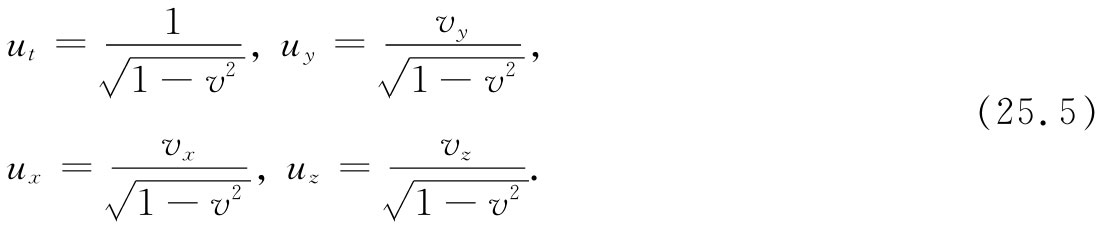
这个四维速度是一个有用的量,例如,可以写出
pμ =m0 uμ . (25.6)
这是相对论中正确的方程都必须具有的那一种典型形式,式的每一边都是一个四维矢量(右边是一个不变量乘以一个四维矢量,那仍然是一个四维矢量)。