
我们已发现势ϕ和A合起来看便形成一个称为Aμ 的四维矢量,而波动方程——即用那些jμ 来确定Aμ 的完整方程组——可写成如式(25.22)那样的方程。这个方程,与电荷守恒律、即式(25.19)一起,就给出了电磁场的基本定律:

只在页面的一个微小区间内就有了全部麦克斯韦方程组——优美而又简单。除了它们既优美而又简单外,将方程组这样写出来从中学习到什么东西呢?首先,这与我们过去将各种不同分量全都写出来时所得到的那些结果有何区别?能否从这一方程推导出某些过去由电荷和电流表示势的波动方程不能够推导出来的东西?答案是明确否定的。我们所做的唯一事情就是改变各事情的名称——应用新的符号表示法。我们已写下了一个方框符号来代表微商,但它仍然意味着不多不少的对时间的二次微商、减去对x的二次微商、减去对y的二次微商、减去对z的二次微商。而μ则意味着有四个方程,对于μ=t,x,y或z会各有一个。那么,可以将那些方程写成这么简洁形式的事实有什么意义呢?按直接从其导出什么东西的观点来看,它确实没有什么意义。然而,也许这些方程的简单性就意味着自然界也具有某种简单性。
让我们来向你证明某种新近才发现的有趣事情:所有物理规律都可以包括在一个方程之中 。这方程就是
U=0. (25.30)
多么简单的一个方程!当然,还需要知道该符号指的是什么。U是一个称为情况的“超脱性”的物理量,而对于它我们有一个公式。这里关系到你怎样去计算该超脱性。你可以取所有已知的物理定律,并把它们都写成一种独特形式。例如,假设你所取的是力学定律F=ma,并把它重新写成F-ma=0。然后你可以将(F-ma)——那当然应该等于零的——叫作力学上的“失调”。其次,你再取这失调的平方 并叫它作U1 ,这可以称为“力学效应的超脱性”。换句话说,你会取
U1 =(F-ma)2 . (25.31)
现在你又写下另一个物理定律,比如说,▽·E=ρ/∈0 ,并定义
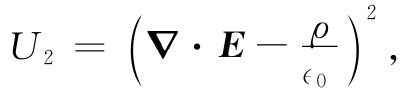
这或许被你称为“电的高斯超脱性”。你继续再写出U3 ,U4 ,等等——对每一物理定律都有一个。
最后,你把来自一切有关的分现象的诸多不同超脱性Ui 都相加起来,而把它叫作宇宙的总 超脱性U,也就是,U=∑Ui 。这样自然界的伟大定律为
U=0. (25.32)
这一“定律”当然意味着所有各个失调的平方之总和为零,而能使一大堆平方之和为零的唯一办法就是其中每一项都等于零。
因此,式(25.32)的“优美简单”定律相当于你原来所写下的一整套方程式。因而绝对明显的是,一种不过把复杂性隐藏在符号的定义之内的简单表示方法并不是真正的简单性。它不过是一种花招 。式(25.32)中所出现的优美——仅从几个方程被隐藏在其中这一事实看来——也不外是花招而已。当你把整个东西都打开时,你就会回到你原来所在的地方。
然而,把电动力学写成式(25.29)那种形式,除了简单之外还有 其他一些东西。它的含义会多一些,就像矢量分析理论含有更多的意义一样。电动力学方程组之所以能够用为洛伦兹变换的四维几何所设计 的那种十分特殊符号写出来——换句话说,作为在四维空间中的一个矢量方程——这一事实,就意味着它在洛伦兹变换下是不变的。只是由于麦克斯韦方程组在那些变换下不变,才使得它们能够被写成优美形式。
能够将电动力学方程组写成式(25.29)那样美妙卓越的形式并非偶然。正是由于在实验上已发现 由麦克斯韦方程组所预言的各种现象在一切惯性系中都相同,相对论才发展起来的。而又是通过研究麦克斯韦方程组的变换性质,才使得洛伦兹发现了他的变换作为保留方程不变的一种变换来说是精确的。
然而,还有另一个要把方程组这样写出来的理由。已经发现——在爱因斯坦猜测方程也许是这样之后——所有 物理定律在洛伦兹变换下都是不变的。这就是相对性原理。因此,如果我们发明一种符号,当写下一个定律时它能够立刻指出该定律是否不变,那么,便能够在试图创立新的理论时保证只写出与相对论原理相一致的方程式。
以这种特殊的符号表示麦克斯韦方程组变得很简单这一事实,并不是什么奇迹,因为这种符号就是在考虑到那些方程之后才发明的。但有意义的物理事情却是:每一个 物理规律 ——介子波的传播或在β衰变中中微子的行为,等等——在相同的变换下都必须具有这种相同的不变性。那么当你待在一艘匀速航行的太空飞船中时,所有自然规律以相同的方法一起作变换,以致没有任何新的现象会发生。正是由于相对论性原理是自然界中的一个事实,所以按照四维矢量的符号世界的各种方程式都会表现得很简单。
[1] 你可能会问:为什么不去考虑
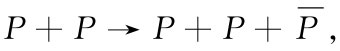
或甚至
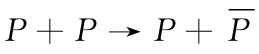
那些显然要求较少能量的反应?答案是,一个称为重子数守恒 的原理告诉我们:“质子数减去反质子数”不能改变,在我们的反应中左边这个量为2,因此,若希望有一反质子出现在右边,则同时应有三个 质子(或其他重子)伴随它。